ЧАСТЬ 2: ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ К ИССЛЕДОВАНИЮ ФУНКЦИЙ. Функции двух переменных

Лекция 11

Функции двух переменных

В этой лекции мы дадим краткий обзор основных понятий математического анализа, связанных с функциями двух переменных. Почти все, что будет изложено, без существенных изменений может быть перенесено на функции n переменных.

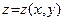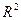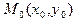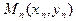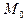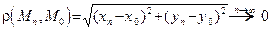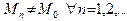Пусть дана функция двух независимых переменных x и y, определенная в некоторой области[1] из . Зафиксируем точку и пусть { } – произвольная последовательность точек, строго стремящаяся к (это означает, что и ). Число b (конечное или бесконечное) называется пределом функци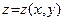и при 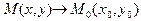, если для любой последовательности { 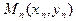}, строго стремящейся к 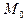, выполняется соотношение: 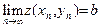. Тот факт, что число b является пределом функци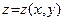и при 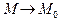, обозначают так: 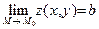. Все свойства 1–8, сформулированные для предела функции одной переменной (см. Часть 1, Свойства предела функции), остаются справедливыми и для функции двух переменных. Функция 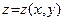называется непрерывной в точке 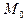, если выполняется равенство: 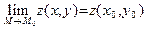. Функция 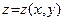называется непрерывной на некотором множестве, если она непрерывна во всех точках этого множества. Все свойства непрерывности 1–6, сформулированные для функции одной переменной (см. Часть 1, Свойства непрерывных функций), также остаются справедливыми и для функции двух переменных.

Остановимся более подробно на теории дифференцирования функций двух переменных. Здесь основная идея такова. Для того, чтобы функцию двух переменных свести к функции одной переменной, одну из переменных (то есть x или y) фиксируют (считают постоянной величиной), а производную вычисляют по другой переменной. Если зафиксирована переменная y (то есть 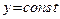), то производная по оставшейся переменной x обозначается 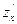или 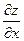и называется частной производной функции 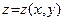по переменной x. Точно так же, если зафиксирована переменная x (то есть 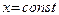), то производная по оставшейся переменной y обозначается 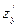или 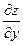и называется частной производной функции 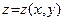по переменной y.

Пример 35. Пусть 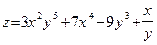. Найдем частные производные этой функции. Сначала зафиксируем переменную y, то есть пусть 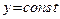. Тогда в первом члене функции z множитель 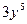является постоянным и может быть вынесен за знак производной. Точно так же в последнем члене множитель 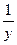является постоянным и также может быть вынесен за знак производной. Третий член является постоянной величиной и поэтому производная от него равна нулю. В итоге получаем:

.

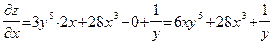Теперь зафиксируем переменную x, то есть пусть 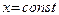. Тогда в первом члене функции z множитель 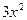является постоянным и может быть вынесен за знак производной. Точно так же в последнем члене множитель 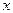является постоянным и также может быть вынесен за знак производной. Второй член является постоянной величиной и поэтому производная от него равна нулю. Получаем:

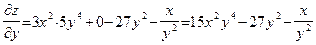. œ

Пример 36. Вычислим частные производные функции 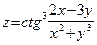. Пусть сначала 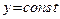. Применяя правило дифференцирования сложной функции, получаем:

.

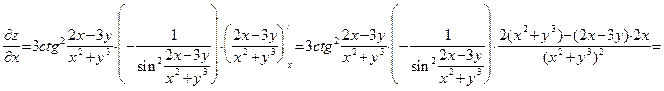
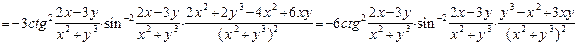Точно так же, считая, что 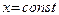, получаем:

€

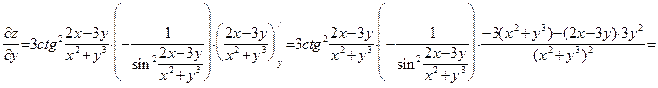
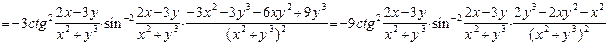
Пример 37. Вычислим частные производные функции 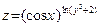. При условии 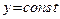показатель данной функции постоянен, следовательно данную функцию нужно дифференцировать как степенную функцию (где 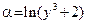; см. Вводная лекцию, Таблица производных элементарных функций). Имеем:

.

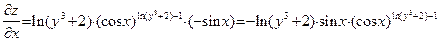Наоборот, если 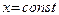, то основание исходной функции постоянно, следовательно данную функцию нужно дифференцировать как показательную функцию (где 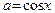; см. Вводная лекцию, Таблица производных элементарных функций). Получаем:

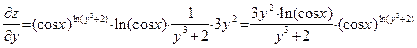. œ

Дадим теперь более формальное определение частных производных.

Определение 21. Частные производные 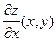и 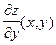функции 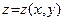, вычисленные в точке 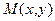, определяются формулами:

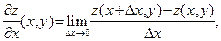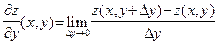		.	(33)
	€

Легко видеть, что эти формулы в точности соответствуют описанной выше процедуре нахождения частных производных. Правила дифференцирования 1–5, записанные нами для функции одного переменного (см. Вводная лекция, Правила дифференцирования), полностью сохраняются и для функций двух переменных. Видоизменяется только цепное правило. Перед тем, как сформулировать соответствующий результат, заметим, что после вычисления частных производных те переменные, которые перед дифференцированием были "заморожены", "размораживаются" и, таким образом, функци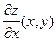и и 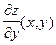опять можно рассматривать как функции двух переменных.

Теорема 27. (цепное правило для функции двух переменных). Предположим, что функция 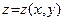имеет непрерывные частные производные 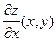и .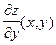

1) Если внутрь функции 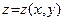вставить дифференцируемые функци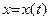и и 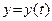, то сложная функция 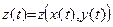будет дифференцируема и ее производная вычисляется по формуле:

.

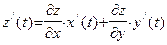(34)

2) Если внутрь функции 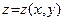вставить функци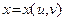и и 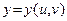, обладающие частными производными, то сложная функция 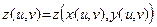также будет иметь частные производные, вычисляемые по формулам:

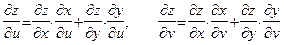	.	(35)
	€

Определение 22. Частные производные второго порядка функции 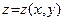определяются формулами:

.

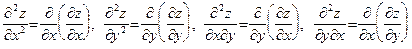(36)

Последние две производные называются смешанными частными производными.

€

Пример 38 (продолжение примера 35). Имеем:

,

.

€

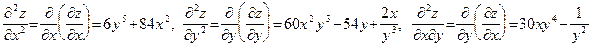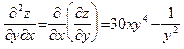В примере 38 мы получили совпадение смешанных производных второго порядка. О закономерности такого результата говорит следующая

Теорема 28. Пусть функция 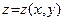обладает непрерывными смешанными производным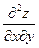и и 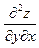. Тогда = .

€

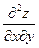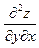Определение 23. Пусть 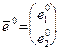– единичный вектор (см. ЛЛААГ, определение 21) и пусть 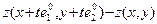есть приращение функции 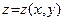в направлении вектора 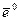. Если существует конечный предел 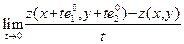, то этот предел называется производной функции 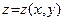в направлении вектора 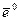и обозначается .

€

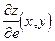Сравнивая определение 23 с определением 21, видим, что при 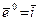(то есть когда вектор 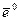имеет направление оси Ox) 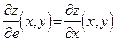, а при 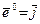(то есть когда вектор 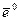имеет направление оси Oy) .

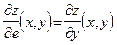Теорема 29. Пусть функция 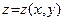определена в области, содержащей точку 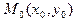, и имеет в этой области непрерывные частные производные. Тогда

,

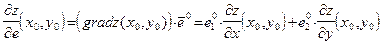(37)

где 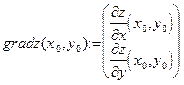– вектор, называемый градиентом функции 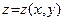в точке .

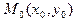Доказательство. Обозначим 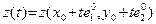. Из определения 23 легко следует, что 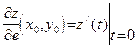. Применяя формулу (34), получаем:

.

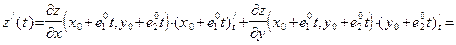
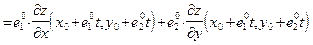Следовательно, 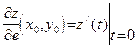= 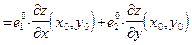. œ

Пример 39. Найдем 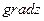и 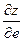в точке 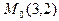по направлению вектора 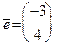, если 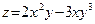. Сначала вычисляем частные производные: 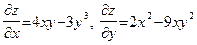. Следовательно, 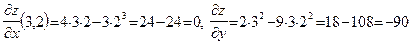. То есть 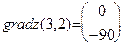. Далее, пронормируем вектор 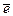, то есть запишем вектор 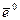, имеющий единичную длину и направление, совпадающее с направлением вектора 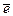(см. ЛЛААГ, пример 14): 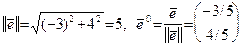. По формуле (37):

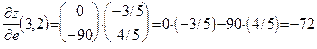. œ