Линейно зависимые и независимые системы функций. Определитель Вронского и его свойства.

Пусть имеем конечную систему из 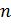функций 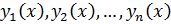, определенных на интервале 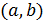. Функции 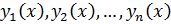называют линейно зависимыми на интервале 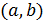, если существуют постоянные 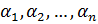, не все равные нулю, такие, что для всех значений 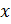из этого интервала справедливо тождество

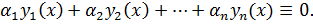
Если же это тождество выполняется только при 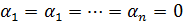, то ф – ии 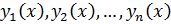называют линейно независимыми на интервале .

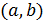Пусть 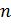ф – ий 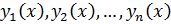имеют производные 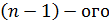порядка. Определитель

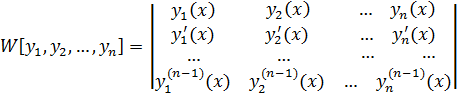
Называется определителем Вронского для этой системы функций. Определитель Вронского является ф – ей от 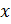, определенной в некотором интервале.

19. Структура общего решения линейного ОДУ n-порядка. Свойства линейного дифференциального оператора n-порядка. Принцип суперпозиции.

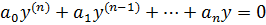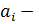Имеем ур – ие , где вещественные постоянные, .
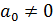Для нахождения общего решения составим характеристическое ур – ие:

.

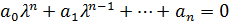Вид общего решения зависит от типа корней:

1. 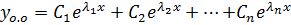, 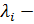вещественные и различные.

2. 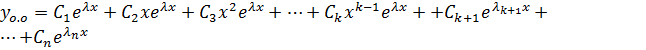, 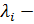вещественные, но среди них есть кратные ( 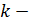кратных и ).

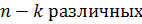3. 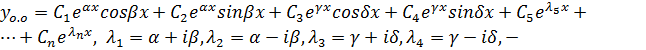комплексные, остальные – вещественные.

4.

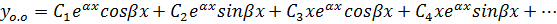
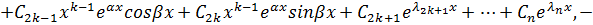
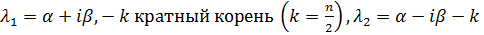кратный корень.

Линейным дифференциальный оператор n -го порядка:

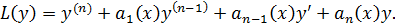
Принцип суперпозиции основан на следующих свойствах решений линейных уравнений:
а) Если 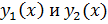— два решения однородного линейного уравнения 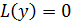, то их линейная комбинация 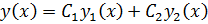при любых постоянных 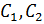является решением однородного уравнения.
б) Если 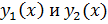— два решения неоднородного линейного уравнения
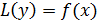, то их разность 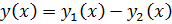является решением однородного уравнения .
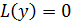в) Любое решение неоднородного линейного уравнения 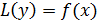есть сумма частного (фиксированного) решения неоднородного уравнения и некоторого решения однородного уравнения.

Принцип суперпозиции:
Если 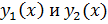— решения неоднородных линейных уравнени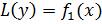й
и 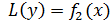, то их сумма 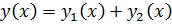является решением уравнения
.

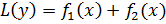20. Линейные ОДУ с переменными коэффициентами. Нахождение общего решения для уравнения 2-го порядка с переменными коэффициентами по одному известному частному решению.

Если известно частное решение 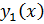ур – ия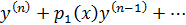

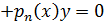, то можно понизить его порядок на единицу, не нарушая линейности ур – ия, полагая 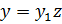, где 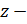новая неизвестная ф – ия, сделав затем замену 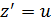или сразу .

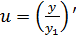Если известно 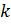частных л.н.з. решений, то порядок ур – ия можно понизить на 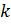единиц.

Для ур – ия 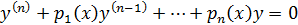общее решение таково:

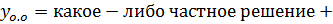общее решение соответствующего однородного ур – ия.

Для нахождения общего решения неоднородного ур - ия при известной фундаментальной системе используется метод Лагранжа (метод вариации постоянных).

Для ур – ия 2 – го порядка:

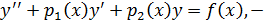общий вид ур – ия второго порядка.

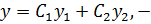вид общего реш –ия соответствующего однородного ур – ия.

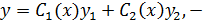вид реш – ия неоднородного ур – ия, 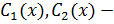некоторые неизвестные ф – ии. Для их определения составляется система:

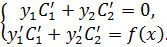
Тогда 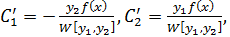где 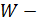определитель Вронского.