Определитель Вронского. Общие теоремы

Линейные дифференциальные уравнения первого порядка.Метод Бернулли

Дифференциальные уравнения вида 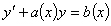называются линейными. Существуют несколько методов их решения: метод Бернулли, метод Лагранжа, метод интегрирующего множителя.
МетодБернулли
Решение уравнения 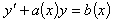ищется в виде 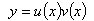. При этой замене получаем: 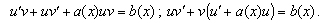Функцию 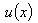выбирают из условия 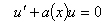.Полученную функцию 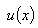подставляют в уравнение 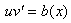(учитываем 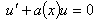), решая которое находят функцию .

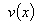Однородные уравнения первого порядка.

Дифференциальное уравнение первого порядка

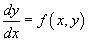
называется однородным, если правая часть удовлетворяет соотношению

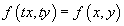
для всех значений t. Другими словами, правая часть должна являться однородной функцией нулевого порядка по отношению к переменным x и y:

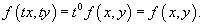
Однородное дифференциальное уравнение можно также записать в виде

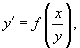
или через дифференциалы:

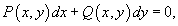
где P(x,y) и Q(x,y) − однородные функции одинакового порядка.

Определение однородной функции

Функция P(x,y) называется однородной функцией порядка n, если для всех t > 0 справедливо следующее соотношение:

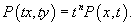
32.Линейная зависимость и независимость системы функций на интервале.Функции y₁(x), y₂(x), ..., y_n(x), определённые на отрезке [a;b], называются линейно зависимыми на [a;b] , если существуют постоянные α₁, α₂, ..., α_n , не равные нулю одновременно и такие, что α₁y₁(x) + α₂y₂(x) + ... + α_ny_n(x) = 0 для всех x из отрезка [a;b]. В противном случае функции y₁(x), y₂(x), ..., y_n(x) называются линейно независимыми.

Линейную зависимость и линейную независимость функций определяют также на (a;b) , (a;b] , [a;b) , на бесконечных промежутках.

Справедливо следующее утверждение.

Функции y₁(x), y₂(x), ..., y_n(x) линейно зависимы на отрезке [a;b] тогда и только тогда, когда хотя бы одна из них является на этом отрезке линейной комбинацией других .

Очевидны следующие утверждения.

• Если среди функций y₁(x), y₂(x), ..., y_n(x) есть нулевая функция, то функции линейно зависимы.

• Если функции y₁(x), y₂(x), ..., y_k(x) линейно зависимы, то при любых y_{k + 1}(x), y_{k + 2}(x), ..., y_n (x) функции y₁(x), y₂(x), ..., y_k(x), y_{k + 1}(x), ..., y_n(x) также линейно зависимы.

• Если функции y₁(x), y₂(x), ..., y_n(x) линейно зависимы на отрезке [a;b] , то они линейно зависимы и на любом отрезке, лежащем внутри [a;b] .

• Если функции y₁(x), y₂(x), ..., y_n(x) линейно независимы на [a;b] , то они линейно независимы и на любом отрезке, содержащем отрезок [а;b] (если, они определены на этом отрезке).

Определитель Вронского. Общие теоремы

Дадим признак линейной независимости n частных решений однородного линейного уравнения n-го порядка. С этой целью введем в рассмотрение определитель, составленный из данных частных решений и их производных до порядка n – 1 включительно:

W(x) =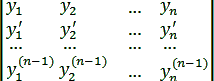

Этот определитель называется определителем Вронского решений y₁, y₂, …, y_n.

Теорема. Для того чтобы решения были линейно независимы в (a, b), т. е. в интервале непрерывности коэффициентов уравнения L(y) = 0, необходимо и достаточно, чтобы W(x) не обращался в нуль ни в одной точке из (a, b).

Значение определителя Вронского n решений однородного линейного уравнения L(y) = 0 тесно связано с самим уравнением, а именно: имеет место следующая формула Остроградского—Лиувилля:

W(x) = W(x₀) .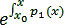

Из формулы видно, что определитель Вронского n решений уравнения L(y) = 0 обладает двумя замечательными свойствами:

1. Если W(x) обращается в нуль в одной точке из интервала (a, b), то он равен нулю во всех точках этого интервала.
2. Если W(x) не равен нулю в одной точке из интервала (a, b), то он отличен от нуля во всех точках этого интервала.

Таким образом, для того, чтобы n решений составляли фундаментальную систему решений уравнения L(y) = 0 в интервале (a, b), достаточно, чтобы их определитель Вронского был отличен от нуля в одной точке x₀ ∈ (a, b).