Тема 10. Дифференциальные уравнения и их системы

Основные понятия и определения. Дифференциальные уравнения первого порядка: уравнения с разделяющимися переменными, линейные неоднородные дифференциальные уравнения; однородные дифференциальные уравнения; дифференциальные уравнения, приводящиеся к однородным; уравнение Бернулли. Задача Коши. Теорема существования и единственности. Дифференциальные уравнения, допускающие понижение порядка. Линейные дифференциальные уравнения второго порядка: однородные дифференциальные уравнения; неоднородные дифференциальные уравнения. Структура общего решения неоднородного дифференциального уравнения второго порядка. Решение однородного дифференциального уравнения второго порядка. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Применение дифференциальных уравнений при решении прикладных задач.

Методические рекомендации

Многочисленные задачи естествознания, техники, механики, биологии, химии и других отраслей знаний сводятся к тому, что по заданным свойствам некоторого процесса или явления необходимо найти математическую модель самого процесса в виде формулы, связывающей переменные величины, т.е. в виде функциональной зависимости.

При изучении таких задач используют дифференциальные уравнения. В данной теме рассмотрены обыкновенные дифференциальные уравнения.

Литература: /2, глава 9 §1-5/, или /4, глава 15 §1-4/, или /5(ч.2), глава 4/.

Вопросы для подготовки к экзамену:

1. Дифференциальные уравнения первого порядка. Общее и частное решения. Задача Коши. Формулировка теоремы существования и единственности решения задачи Коши.

2. Интегрирование простейших типов дифференциальных уравнений первого порядка. Дифференциальные уравнения с разделяющимися переменными.

3. Однородные дифференциальные уравнения первого порядка.

4. Линейные дифференциальные уравнения первого порядка.

5. Дифференциальные уравнения высших порядков. Формулировка теоремы существования и единственности решения задачи Коши.

6. Дифференциальные уравнения, допускающие понижение порядка.

7. Линейные дифференциальные уравнения второго порядка. Однородные уравнения. Свойства их решений. Фундаментальная система решений.

8. Теорема о структуре общего решения линейного однородного дифференциального уравнения.

9. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

10. Линейные неоднородные дифференциальные уравнения. Теорема о структуре общего решения.

11. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами и правой частью специального вида.

12. Понятие о системах линейных дифференциальных уравнений первого порядка.

Тема 11. Кратные, криволинейные и поверхностные интегралы.

Векторный анализ

Определение двойного интеграла, геометрический и физический смысл. Свойства двойного интеграла. Криволинейные координаты на плоскости. Полярные и эллиптические координаты. Замена переменных в двойном интеграле. Приложения двойного интеграла к вычислению площадей плоских фигур и объемов тел. Тройной интеграл, геометрический и физический смысл. Сведение тройного интеграла к повторному. Замена переменных в тройном интеграле. Сферические и цилиндрические координаты. Скалярное поле. Производная по направлению. Градиент скалярного поля, его свойства. Векторное поле. Поток вектора. Дивергенция векторного поля. Циркуляция. Ротор векторного поля. Соленоидальное поле. Теоремы Остроградского-Гаусса и Стокса в векторной форме. Связь между характеристиками векторных полей.

Методические рекомендации

При изучении физики, механики и при решении разнообразных инженерных задач часто возникает необходимость наряду с интегралами от действительной функции одного переменного рассматривать интегралы от функций многих переменных. Эти интегралы приходиться вычислять по двумерным, трехмерным областям, по кривым и поверхностям. Такие интегралы играют важную роль при исследовании скалярных и векторных полей, задаваемых в пространстве действительными и векторными функциями векторного аргумента, составляющими предмет изучения теории поля и векторного анализа.

Примерами векторных полей являются поле скоростей текущей жидкости, поле скоростей точек твердого тела, вращающегося с угловой скоростью или вокруг данной оси, поле электрической или магнитной напряженности и другие.

Литература: /2, глава 7 §5-10/, или /4, глава 13 §1-14/, или /5(ч.1), главы 1,2/.

Вопросы для подготовки к экзамену:

1. Задачи, приводящие к двойным интегралам. Двойной интеграл.

2. Свойства двойного интеграла.

3. Вычисление двойного интеграла в прямоугольных декартовых координатах.

4. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.

5. Приложения двойного интеграла.

6. Тройной интеграл.

7. Замена переменных в тройном интеграле. Тройной интеграл в цилиндрических и сферических координатах.

8. Приложения тройного интеграла.

9. Задачи, приводящие к понятию криволинейного интеграла. Криволинейный интеграл первого рода.

10. Криволинейный интеграл второго рода. Связь между криволинейными интегралами первого и второго рода.

11. Приложения криволинейных интегралов. Формула Грина.

12. Формула Стокса. Формула Остроградского.

13. Дивергенция векторного поля.

14. Ротор векторного поля.

15. Поток векторного поля.

16. Работа векторного поля.

17. Потенциальные и соленоидальные поля.

Тема 12. Ряды

Числовой ряд. Сумма ряда. Свойства сходящихся рядов. Необходимый признак сходимости ряда. Сравнение рядов с положительными членами. Признаки сходимости Даламбера, Коши, интегральный. Знакочередующийся ряд. Абсолютная и условная сходимость. Функциональные ряды. Признак равномерной сходимости. Свойства равномерно сходящихся рядов. Степенные ряды. Радиус сходимости. Свойства сходящихся рядов. Ряды Тейлора и Маклорена. Примеры разложений. Применение рядов в приближенных вычислениях. Ряды Фурье (для функций с периодом 2p и 2l). Разложение четных и нечетных функций, непериодических функций.

Методические рекомендации

Ряды являются обобщением обычных сумм и многочленов на бесконечное число слагаемых. Для изучения рядов используется частный случай функций: функций натурального аргумента – последовательностей – и их пределов при n→∞, понятие о которых дается в курсе дифференциального исчисления. Введение рядов позволяет изучать функции, не являющиеся элементарными, находить интегралы, которые невозможно вычислить методами, описанными в курсе интегрального исчисления. В дальнейшем ряды находят применение в курсе теории вероятностей.

Литература: /2,глава 8 §1-5/, или /4, глава14 §1-7/, или /5(ч.1),глава 3/.

Вопросы для подготовки к экзамену:

1. Сходимость и сумма ряда. Необходимое условие сходи­мости ряда.

2. Теоремы сравнения.

3. Признаки Даламбера и Коши.

4. Интегральный признак сходимости ряда.

5. Теорема Лейбница. Оценка остатка знакочередующегося ряда.

6. Теорема о сходимости абсолютно сходящегося ряда. Свойст ва абсолютно сходящихся рядов.

7. Понятие равномерной сходимости. Признак Вейерштрасса.

8. Теорема о непрерывности суммы функционального ряда.

9. Теоремы о почленном интегрировании и почленном диф­ференцировании функционального ряда.

10.Теорема Абеля. Интервал и радиус сходимости степенно­го ряда.

11.Теорема о равномерной сходимости степенного ряда. Непрерывность суммы ряда.

12.Почленное интегрирование и дифференцирование сте­пенных рядов.

13.Разложение функции в степенной ряд. Ряд Тейлора.

14.Разложение по степеням 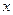бинома .

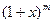15.Условия разложимости функции в ряд Тейлора.

16.Разложение по степеням 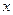функций .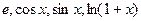