Дифференциальные уравнения движения механической системы.

Центр масс механической системы. Координаты центра масс.

Система центра масс — система отсчёта, относительно которой центр масс механической системы неподвижен. Рассмотрим произвольную механическую систему твердых тел с заданным взаимным расположением в пространстве и с известными массами. Поступательное движение такой системы под действием внешних сил эквивалентно движению материальной точки, имеющей массу, равную массе системы, и находящейся под воздействием результирующей силы всех внешних сил.

Геометрическую точку, в которой располагается эта материальная точка, называют центром инерции или центром масс данной системы. Для произвольной неподвижной прямоугольной системы координат (ее называют также лабораторной системой) координаты центра масс определяются следующими формулами:

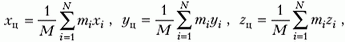
где m_i, x_i, y_i, z_i – массы и координаты центров масс тел, входящих в систему, а M – суммарная масса всех тел.

Если сумма внешних сил, действующих на систему, равна нулю, то центр масс остается неподвижным или движется прямолинейно с некоторой постоянной скоростью (в зависимостиот предыстории). В этом случае удобно рассматривать движение тел под действием внутренних сил в инерциальной системе отсчета, связанной с центром масс. В такой системе отсчета импульс системы равен нулю и будет оставаться нулевым при любых взаимодействиях между телами системы.

Перейдем к разбору конкретных задач.

52. момент инерции твердого тела. Радиус инерции.

Момент инерции тела относительно оси. Радиус инер­ции.

Положение центра масс характеризует распределение масс системы не полностью. Например (рис.32), если расстояния h от оси Oz каждого из одинаковых шаров А и В увеличить на одну и ту же величину, то положение центра масс системы не изменится, а распределение масс станет другим, и это скажется на движении системы (вращение вокруг оси Oz при прочих равных условиях будет происходить медленнее).

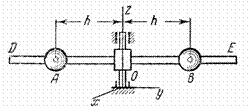
Рис.32

Поэтому в механике вводится еще одна характеристика распре­деления масс - момент инерции. Моментом инерциитела (системы) относительно данной оси Oz (или осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний от этой оси

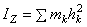
Из определения следует, что момент инерции тела (или системы) относительно любой оси является величиной положительной и не равной нулю.

Заметим также, что момент инерции тела – это геометрическая характеристика тела, не зависящая от его движения.

Осевой момент инерции играет при вращательном движении тела такую же роль, какую масса при поступательном, т.е. что осевой момент инерции является ме­рой инертности тела при вра­щательном движении.

Согласно формуле момент инерции тела равен сумме момен­тов инерции всех его частей от­носительно той же оси. Для од­ной материальной точки, нахо­дящейся на расстоянии h от оси, .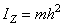

Часто в ходе расчетов пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси Оz называется линейная величина 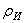, определяемая равенством

,

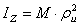где М - масса тела. Из определения следует, что радиус инерции геометрически равен расстоянию от оси Оz той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела.

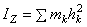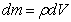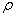В случае сплошного те­ла, разбивая его на элементарные части, найдем, что в пределе сумма, стоящая в равенстве , обратится в интеграл. В результате, учи­тывая, что , где - плотность, а V-объем, получим

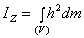или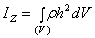

Интеграл здесь распространяется на весь объем V тела, а плотность 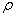и расстояние h зависят от координат точек тела.

Моменты инерции некоторых однородных тел:

1.Тонкий однородный стержень длины l и массы М. Вычислим его момент инерции относи­тельно оси Аz, перпендикулярной к стержню и прохо­дящей через его конец А (рис. 33).

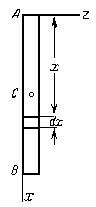
Рис.33

Направим вдоль АВ координатную ось Ах. Тогда для любого элементарного отрезка длины dx величина h=x, а масса 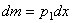, где 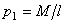- масса единицы длины стержня. В результате

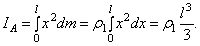
Заменяя здесь 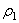его значением, найдем окончательно:

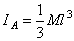
2. Тонкое круглое однородное кольцо радиуса R и массы М. Найдем его момент инерции относительно оси Cz, перпендикулярной плоскости кольца и проходящей через его центр (рис.34,а). Так как все точки кольца находятся от оси Cz на расстоянии h_k=R, то

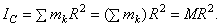
Следовательно, для кольца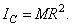

Очевидно, такой же результат получится для момента инерции тонкой цилиндрической оболочки массы М и радиуса R относитель­но ее оси.

3. Круглая однородная пластина или цилиндр ра­диуса R и массы М. Вычислим момент инерции круглой пла­стины относительно оси Сz, перпендикулярной к пластине и прохо­дящей через ее центр (см. рис.34,а). Для этого выделим элементарное кольцо радиуса r и ширины dr (рис.34,б).

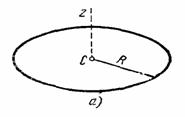
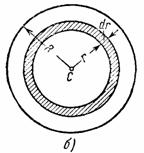
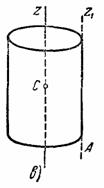
Рис.34

Площадь этого кольца равна 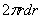, а масса 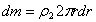, где 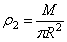- масса единицы площади пластины. Тогда для выделенного элементарного кольца будет

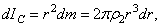
а для всей пластины 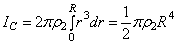. Заменяя здесь 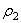его значением, найдем окончательно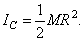

Такая же формула получится, очевидно, и для момента инерции 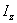однородного круглого цилиндра массы М и радиуса R относительно его оси Оz (риc.34,в).

4. Прямоугольная пластина, конус, шар. Опуская выкладки, приведем формулы, определяющие моменты инерции следующих тел:

а) сплошная прямоугольная пластина массы М со сторонами АВ = а и BD = b (ось х направлена вдоль стороны AB, ось у - вдоль BD):

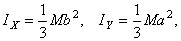
б) прямой сплошной круглый конус массы М с радиусом основания R (ось z направлена вдоль оси конуса):

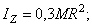
г) сплошной шар массы М и радиуса R (ось z направлена вдоль диаметра):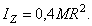

53. Моменты инерции тела относительно параллельных осей. Теорема Гюйгенса.

Моменты инерции данного тела относи­тельно разных осей будут, вообще говоря, разными. Покажем, как зная момент инерции относительно какой-нибудь одной оси, проведен­ной в теле, найти момент инерции от­носительно любой другой оси, ей па­раллельной.

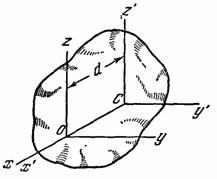
Рис.35

Проведем через центр масс С тела произвольные оси Cx'y'z', а через лю­бую точку О на оси Сх' - оси Oxyz, такие, что Оy½½Сy', Oz½½Cz' (рис. 35). Расстояние между осями Cz' и Оz обозначим через d. Тогда

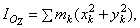
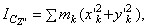
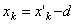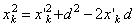но, как видно из рисунка, для любой точки тела или , а 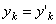. Подставляя эти значения 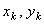, в выражение для 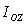и вынося общие множители d ² и 2d за скобки, получим

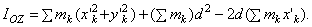
В правой части равенства первая сумма равна I_cz', а вторая - массе тела М. Найдем значение третьей суммы. На основании фор­мул для координат центра масс 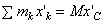.Так как в на­шем случае точка С является началом координат, то x_C = 0 и, сле­довательно, 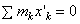. Окончательно получаем:

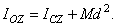
Формула выражает следующую теорему Гюйгенса:

Момент инерции тела относительно данной оси равен моменту инерции относительно оси, ей параллельной, проходящей через центр масс тела, сложенному с произведением массы всего тела на квадрат расстояния между осями.