Нормальное распределение случайных величин

Также называют гауссовским распределением, удобен для анализа, часто встречается на практике, особенно для анализа помех в каналах связи.

По этому закону плотность вероятности Р(х):

Р(х)=1/( σ_x )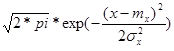

График плотности Р(х)

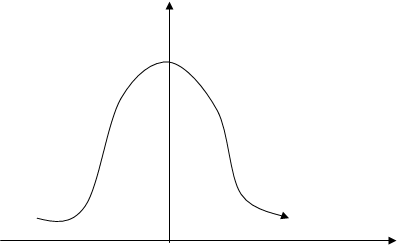х

Когда m_x=0 и σ_x=1

Если изменяется σ_x, то меняется сама кривая (становится более вытянутой по ОУ)

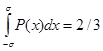- вероятность, что случайная величина не выйдет за пределы 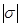составляет примерно 2/3.

Распространено нормальное распределение, т.к. при суммировании достаточно большого числа равномерных статистически независимых случайных величин, которые имеют произвольные плотности распределения, у них плотность распределения суммы

Любой сигнал, который подвергается обработке в какой-то степени является случайным сигналом, который изменяется по времени и по частоте. Последовательность X(nT) является случайной, если каждый ее элемент является случайной величиной.

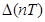- помеха

X(nT) Y(nT)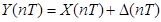

Характеристики:

1) Математическое ожидание.

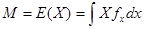где Е(Х)- математическое усреднение сл. величины Х

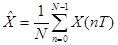
Х(nТ)

N-1 N

2) Дисперсия.

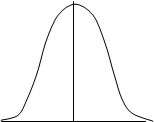
Дисперсия сигнала для непрерывной случайной величины определяется так:

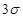0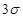

95%

3) Авто корреляция.

Корреляция – связь между нынешним и предыдущим состоянием.

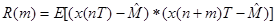
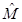- среднее значение или математическое ожидание.

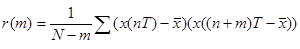
Авто корреляционная функция является мерой связей между случайными последовательностями. Если значение r(m)=0, то нет никакой связи межу случайными последовательностями.

4) Спектральная плотность или мощность стационарной случайной последовательности.

Спектральная плотность сигнала ----- есть средняя мощность последовательности ----- , приходящейся на достаточно узкую полосу частот.

Эта функция связана с преобразованием Фурье, и имеет следующий вид:

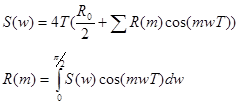
Любой сигнал, который подвергается обработке в какой-то степени является случайным сигналом, который изменяется по времени и по частоте. Последовательность X(nT) является случайной, если каждый ее элемент является случайной величиной.

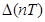- помеха

X(nT) Y(nT)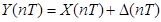

Характеристики:

1) Математическое ожидание.

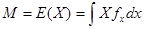
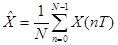
Х(nТ)

N-1 N

2) Дисперсия.

Дисперсия сигнала для непрерывной случайной величины определяется так:

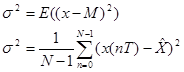
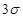0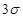

95%

3) Авто корреляция.

Корреляция – связь между нынешним и предыдущим состоянием.

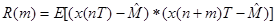
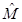- среднее значение или математическое ожидание.

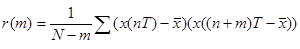
Авто корреляционная функция является мерой связей между случайными последовательностями. Если значение r(m)=0, то нет никакой связи межу случайными последовательностями.

4) Спектральная плотность или мощность стационарной случайной последовательности.

Спектральная плотность сигнала ----- есть средняя мощность последовательности ----- , приходящейся на достаточно узкую полосу частот.

Эта функция связана с преобразованием Фурье, и имеет следующий вид:

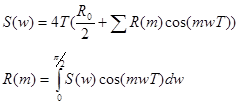
Контрольные вопросы:

1. Понятие случайные сигналы и их ансамбль реализаций
2. Как строятся модели случайных процессов?
3. Равномерное распределение случайных величин
4. Каковы вероятностные характеристики случайного процесса?

Тема 6.Дискреттеу және кванттау. Есептің жалпы қойылуы. Котельников теоремасы.

Цель лекции: Изучить дискретизацию и квантирование.

Вопросы:

1. Классификация методов дискретизации

2. Квантирование информации

3. Базисные функции

4. Квантирование по степени

Ақпаратты кванттау

X, Т жинакталған кординаталар жүйесіндегі үздіксіз сиганалдар үздіксіз функциялармен x(t) белгіленеді. Уқсас көрсететін сигналынан цифрлыққа өту сигналдың уақыт және деңгейі бойынша квантталуымен (дискретизациясымен) x(t) байланысты.

Ақпаратты беру, сақтау және өңдеу үшін қолданылады.

Дискретизация әдістерін классификациялау.

Дискретизация әдістерін келесі белгілермен өтуі мүмкін.

Уақыт боиынша кванттау - дискретизация;

1) есептеу жиілігі;

2) дискреттеу және қалпына келтіру дәлдік бағасының критерий;

3) базистік функциялар;

4) жақындау принципі;