Метод регуляризации А.Н.Тихонова
Основы общей теории.
Метод регуляризации А.Н.Тихоновавключает в себя большую группу схем решения задачи (1), отличительной особенностью которых является использование стабилизирующего функционала.
Наличие погрешности 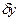 в наблюдаемой
в наблюдаемой 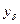 делает естественным выбор искомого решения х среди элементов, удовлетворяющих неравенству:
делает естественным выбор искомого решения х среди элементов, удовлетворяющих неравенству:
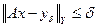 . (4.15)
. (4.15)
Для устойчивого выделения единственного элемента из допустимых, с точки зрения (15), следует ввести принцип отбора. В качестве такого можно принять требование минимума заданного функционала 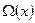 . Задача нахождения приближенного решения (1) оказывается, таким образом, следующей:
. Задача нахождения приближенного решения (1) оказывается, таким образом, следующей:
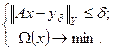 (4.16)
(4.16)
Если оператор А, функционал 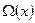 таковы, что приемлем принцип Лагранжа, то из (16) получаем:
таковы, что приемлем принцип Лагранжа, то из (16) получаем:
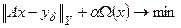 , (4.17)
, (4.17)
где  – параметр, который надо выбрать, например, из требования того, чтобы для найденной экстремали
– параметр, который надо выбрать, например, из требования того, чтобы для найденной экстремали 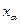 для (17) выполнялось неравенство:
для (17) выполнялось неравенство:
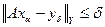 .
.
Функционал 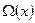 называют стабилизирующим, поскольку его назначение - обеспечить устойчивость нахождения решения задачи
называют стабилизирующим, поскольку его назначение - обеспечить устойчивость нахождения решения задачи 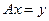 .
.
Если, например, в качестве оператора А выступает интеграл Пуассона (задача редукции с ядром 1 из (3)), то принципом отбора решений из класса допустимых может служить требование наибольшей гладкости решения.
В содержательной записи (15) , если 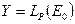 , для этого случая примет вид:
, для этого случая примет вид:
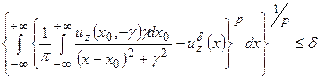 (4.18)
(4.18)
Неравенству (18) удовлетворяют как гладкие, так и резко осциллирующие функции 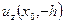 . Отбор среди них более гладких можно формализовать критерием:
. Отбор среди них более гладких можно формализовать критерием:
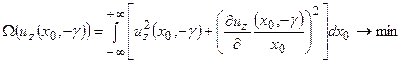 ,
,
Что и служит примером для (16).
Постановка (17) как способ регуляризации может быть получена и с других позиций. Предположим, что множество М, среди элементов которого ищется приближенное решение задачи
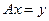 (4.19)
(4.19)
описано так:
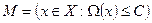
Даже в том случае, если правая часть в (19) известна точно, в силу того, что решение (19) множеству М не принадлежит, решение задачи 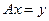 ;
; 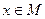 , вообще говоря, не существует. Поэтому переформулируем ее так:
, вообще говоря, не существует. Поэтому переформулируем ее так:
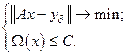 (4.20)
(4.20)
Если оператор А и функционал 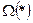 таковы, что к (20) приемлемо правило Лагранжа, то от (20) переходим к (17) с некоторым
таковы, что к (20) приемлемо правило Лагранжа, то от (20) переходим к (17) с некоторым 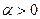 .
.
Таким образом, к задаче (17) приводит как требование минимизации стабилизирующего функционала при заданном уровне невязки, так и минимизации невязки при заданном уровне значения стабилизирующего функционала 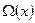 , определяющего множество (например, компактное), на котором ищется решение (19).
, определяющего множество (например, компактное), на котором ищется решение (19).
В приведенных рассуждениях ничего не меняется, если вместо точного оператора А задано его приближение 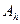 .
.
Обозначим 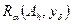 - оператор из
- оператор из 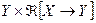 , который доставляет решение задаче (17)
, который доставляет решение задаче (17) 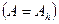 . Метод регуляризации А.Н.Тихонова состоит в таком выборе функционала
. Метод регуляризации А.Н.Тихонова состоит в таком выборе функционала 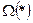 и правила нахождения
и правила нахождения  , в зависимости от
, в зависимости от 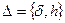 , чтобы
, чтобы 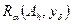 было регуляризирующим семейством операторов для (19). Способов такого выбора много. Приведем некоторые, наиболее характерные из них.
было регуляризирующим семейством операторов для (19). Способов такого выбора много. Приведем некоторые, наиболее характерные из них.
Пусть, как и ранее, точечные данные задачи (19) - 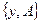 приближенные
приближенные 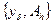 ; L- линейный оператор, действующий из банахова пространства Х в банахово пространство V, и для некоторого
; L- линейный оператор, действующий из банахова пространства Х в банахово пространство V, и для некоторого 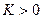 и всех
и всех 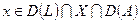 , выполнено неравенство:
, выполнено неравенство:
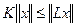 . (4.21)
. (4.21)
В качестве метода регуляризации рассмотрим оператор 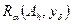 , доставляющий данным
, доставляющий данным 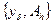 решение задачи:
решение задачи:
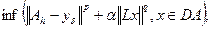 (4.22)
(4.22)
где p, q- целые положительные числа и 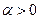 .
.
Следующий результат характеризует алгоритм (22) как регуляризующий.
Если А, 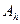 ,L- линейные, замкнутые операторы; Х,Y - рефлексивные пространства; V -равномерно выпукло, выполнено условие (21) для оператора L, и (Аh ,уδ) - приближенные данные, то (22) разрешимо единственным образом, а последовательность решений этой задачи- экстремальных
,L- линейные, замкнутые операторы; Х,Y - рефлексивные пространства; V -равномерно выпукло, выполнено условие (21) для оператора L, и (Аh ,уδ) - приближенные данные, то (22) разрешимо единственным образом, а последовательность решений этой задачи- экстремальных 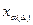 - сходится к решению задачи
- сходится к решению задачи 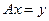 с точными данными (А,
с точными данными (А, 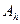 предполагаются взаимно-однозначными) по норме
предполагаются взаимно-однозначными) по норме 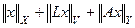 при связи α с ∆ такой, что:
при связи α с ∆ такой, что:
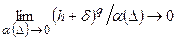 . (4.23)
. (4.23)
Таким образом, алгоритм (22) определяет семейство регуляризующих операторов для задачи 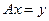 при выборе
при выборе 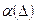 по правилу, обеспечивающему выполнение требование (23).
по правилу, обеспечивающему выполнение требование (23).
Требования, наложенные на оператор, L будут, например, выполнены, если L=I и Х=L2 либо 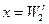 . Смысл этих требований состоит в том, что оператор L, действующий из Х в V, должен иметь ограниченный обратный из V в Х. Однако оказывается, что алгоритм (22) является регуляризирующим и тогда, когда требование (21) не выполнено, но множество:
. Смысл этих требований состоит в том, что оператор L, действующий из Х в V, должен иметь ограниченный обратный из V в Х. Однако оказывается, что алгоритм (22) является регуляризирующим и тогда, когда требование (21) не выполнено, но множество:
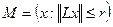
компактно в Х.
Действительно, обращаясь к постановке (20), приходим к необходимости решить задачу:
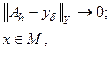 (4.24)
(4.24)
где М - выпуклый компакт. Если А - линеен, взаимно-непрерывен, Y - равномерно выпукло (можно ослабить требования на Y), то задача (24) эквивалентна обращению оператора 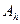 на образе компактного множества М при отображении
на образе компактного множества М при отображении 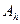 . Но, по теореме о гомеоморфизме (прил.2), Аh-1 , будет непрерывным на Аh(М). Точнее, справедлив такой результат.
. Но, по теореме о гомеоморфизме (прил.2), Аh-1 , будет непрерывным на Аh(М). Точнее, справедлив такой результат.
Пусть, как и ранее 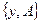 и
и 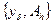 - соответственно, точные и приближенные данные задачи (1). А,
- соответственно, точные и приближенные данные задачи (1). А, 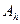 - линейные замкнутые операторы, имеющие обратные (т.е. взаимно-однозначные), Х - банахово пространство, Y и V – рефлексивны. Если линейный, взаимно-однозначный оператор L таков, что для любого
- линейные замкнутые операторы, имеющие обратные (т.е. взаимно-однозначные), Х - банахово пространство, Y и V – рефлексивны. Если линейный, взаимно-однозначный оператор L таков, что для любого 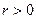 множество
множество 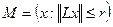 компактно, то задача (22) разрешима единственным образом, и последовательность ее решений
компактно, то задача (22) разрешима единственным образом, и последовательность ее решений 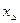 сходится к точному решению (1) по норме пространства Х при связи
сходится к точному решению (1) по норме пространства Х при связи 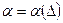 такой, что
такой, что
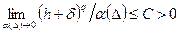 . (4.25)
. (4.25)
Условия (23) и (25) обеспечивают регуляризующие свойства алгоритма 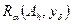 , определенного как решение (22), но еще не позволяют однозначно выбрать величину параметра регуляризации. Один из результатов, позволяющих это сделать, состоит в следующем.
, определенного как решение (22), но еще не позволяют однозначно выбрать величину параметра регуляризации. Один из результатов, позволяющих это сделать, состоит в следующем.
Если все рассматриваемые пространства гильбертовы и 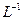 в (22) линеен, взаимно-однозначен и вполне непрерывен, то при выборе
в (22) линеен, взаимно-однозначен и вполне непрерывен, то при выборе  в (22) из условия
в (22) из условия
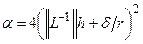 , (4.26)
, (4.26)
алгоритм 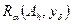 (22) является оптимальным по порядку на множестве
(22) является оптимальным по порядку на множестве
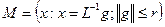 .
.
Условия оптимальности существенно снижают произвол в выборе параметра регуляризации. Однако доказывать эти свойства можно лишь в относительно простых ситуациях. Выделение оптимальных (по точности) и оптимальных по порядку алгоритмов требует априорного формирования множества М, на котором выделяемый алгоритм является оптимальным. Однако конструкция этого множества в большинстве случаев такова (случаи, когда что-то удается доказать), что его введение в большей мере имеет формально-математический характер. Отсюда снижается и ценность самих принципов оптимальности, поскольку они гарантируют оптимальность на формально введенных множествах. Таким образом, оптимальность формальная, доказываемая, не является таковой по существу задачи. Поэтому требования оптимальности при конструкции способов выбора параметра регуляризации отходят на второй план, а на первый выступают физически содержательные принципы его работы. Простейший из них состоит в том, чтобы было выполнено равенство:
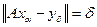 , (4.27)
, (4.27)
где 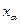 - решение задачи (22). По мере увеличения параметра регуляризации погрешность, получаемая по контролируемой (27) невязке, возрастает, но одновременно возрастает и требование регулярности, заложенное в стабилизирующем функционале. Необходимо добиться компромисса. Надо выделить наиболее устойчивое решение не выходящее за пределы допустимой невязки. Выбор α из этого условия называется принципом невязки. Алгоритмическое дело сводится к перебору значений параметра α от больших значений к меньшим на некотором множестве и выбору такого
- решение задачи (22). По мере увеличения параметра регуляризации погрешность, получаемая по контролируемой (27) невязке, возрастает, но одновременно возрастает и требование регулярности, заложенное в стабилизирующем функционале. Необходимо добиться компромисса. Надо выделить наиболее устойчивое решение не выходящее за пределы допустимой невязки. Выбор α из этого условия называется принципом невязки. Алгоритмическое дело сводится к перебору значений параметра α от больших значений к меньшим на некотором множестве и выбору такого 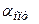 , когда впервые выполняется неравенство:
, когда впервые выполняется неравенство:
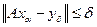 . (3.28)
. (3.28)
Однако здесь не учитывается погрешность в задании самого оператора. Эта погрешность вводит свою дополнительную часть в суммарную невязку и эту часть также надо учитывать. В том случае, когда оператор А известен с ошибкой, т.е. задан 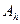 , следует вместо (28) пользоваться правилом обобщенной невязки:
, следует вместо (28) пользоваться правилом обобщенной невязки:
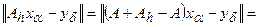
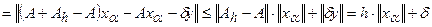 ,
,
алгоритмически дело опять сводится к методу невязки, роль которой в данном случае играет не 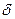 , а обобщенная невязка
, а обобщенная невязка 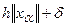 . Алгоритмически вопрос выбора оптимального параметра регуляризации решается перебором величины
. Алгоритмически вопрос выбора оптимального параметра регуляризации решается перебором величины  и получением соответствующих регуляризованных приближений от больших значений
и получением соответствующих регуляризованных приближений от больших значений  к меньшим и остановки тогда, когда впервые будет выполнено неравенство
к меньшим и остановки тогда, когда впервые будет выполнено неравенство
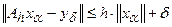 (4.29)
(4.29)
Это значение принимается за оптимальное. В описанных алгоритмах для того, чтобы выбрать параметр регуляризации, требуется знать уровень погрешностей 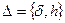 . Если эти погрешности неизвестны, то можно воспользоваться следующим приемом, основанном на рассмотрении “динамики” изменения решения в зависимости от параметра регуляризации.
. Если эти погрешности неизвестны, то можно воспользоваться следующим приемом, основанном на рассмотрении “динамики” изменения решения в зависимости от параметра регуляризации.
Если 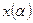 есть решение задачи (22) при произвольном
есть решение задачи (22) при произвольном  , то зависимость величины параметра регуляризации от погрешности можно считать такой, что при отсутствии погрешностей
, то зависимость величины параметра регуляризации от погрешности можно считать такой, что при отсутствии погрешностей 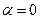 . Тогда точное решение есть
. Тогда точное решение есть 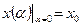 . Разложим
. Разложим 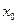 в окрестности
в окрестности 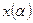 по степеням
по степеням 
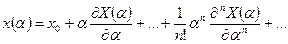
Тогда 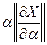 характеризует линейную часть отличия точного решения от приближенного
характеризует линейную часть отличия точного решения от приближенного 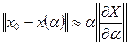 . Требуя, чтобы это отличие было минимальным, приходим к правилу выбора α:
. Требуя, чтобы это отличие было минимальным, приходим к правилу выбора α:
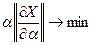 . (4.30)
. (4.30)
Это правило называется квазиоптимальным способом выбора параметра регуляризации.
Приведенные способы выбора параметра регуляризации являются, если так можно выразиться, эталонными. В каждой конкретной задаче их придется модифицировать, приспосабливать к условиям задачи. В некоторых случаях и параметр регуляризации и вид стабилизирующего функционала могут быть найдены из данных самой задачи. Типичный тому пример - Винеровская фильтрация.
