Конспект лекций по обыкновенным дифференциальным уравнениям. ч.3. 2 страница
2) Если 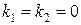 , то возможны два случая:
, то возможны два случая:
1. Общее решение имеет вид 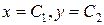 – все точки являются точками покоя, т.е. все решения устойчивы.
– все точки являются точками покоя, т.е. все решения устойчивы.
2. Общее решение имеет вид
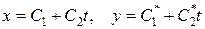 ,
,
где 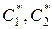 – линейные комбинации постоянных
– линейные комбинации постоянных 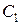 и
и 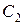 . Точка покоя
. Точка покоя 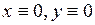 неустойчива.
неустойчива.
Классификация точек покоя тесно связана с классификацией особых точек. Действительно, в рассматриваемом случае система (1), в которой 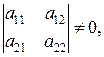 путем исключения
путем исключения  могла быть сведена к уравнению
могла быть сведена к уравнению
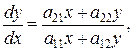 (2)
(2)
Интегральные кривые которого совпадают с траекториями движения системы (1). При этом точка покоя 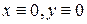 системы (1) является особой точкой уравнения (2).
системы (1) является особой точкой уравнения (2).
Если оба корня характеристического уравнения имеют отрицательную действительную часть (случаи а)1); б)1); в)1)), то точка покоя асимптотически устойчива.
Если же хотя бы один корень характеристического уравнения имеет положительную действительную часть (случаи а)2); а)3); б)2); в)2)), то точка покоя неустойчива.
1.3. Однородная система 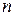 линейных уравнений с постоянными коэффициентами.
линейных уравнений с постоянными коэффициентами.
Для системы n линейных однородных дифференциальных уравнений с постоянными коэффициентами
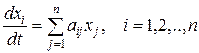 (3)
(3)
проведенный в предыдущей лекции анализ переносится почти без изменений.
Если действительные части всех корней характеристического уравнения системы (3) отрицательны, то тривиальное решение 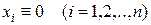 асимптотически устойчиво.
асимптотически устойчиво.
В самом деле, частные решения, соответствующие некоторому корню 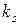 характеристического уравнения, имеют вид
характеристического уравнения, имеют вид
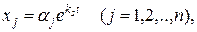
если 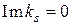 , и
, и
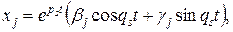
если 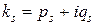 , и, наконец, в случае кратных корней – решения того же вида, но ещё умноженные на некоторые многочлены
, и, наконец, в случае кратных корней – решения того же вида, но ещё умноженные на некоторые многочлены 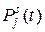 . Очевидно, что все решения такого вида при
. Очевидно, что все решения такого вида при 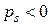 или
или 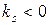 (если
(если 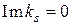 ) стремятся к нулю при
) стремятся к нулю при 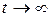 не медленнее, чем
не медленнее, чем 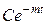 , где
, где 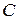 – постоянный множитель, а
– постоянный множитель, а 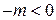 и больше наибольшей действительной части корней характеристического уравнения. Следовательно, при достаточно большом
и больше наибольшей действительной части корней характеристического уравнения. Следовательно, при достаточно большом  точки траекторий, начальные значения которых находятся в любой
точки траекторий, начальные значения которых находятся в любой 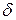 - окрестности начала координат, попадают в сколь угодно малую
- окрестности начала координат, попадают в сколь угодно малую 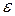 - окрестность начала координат, а при
- окрестность начала координат, а при 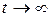 – неограниченно приближаются к началу координат, т.е. точка покоя
– неограниченно приближаются к началу координат, т.е. точка покоя 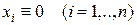 асимптотически устойчива.
асимптотически устойчива.
Если же хотя бы для одного корня характеристического уравнения 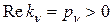 , то соответствующее этому корню решение вида
, то соответствующее этому корню решение вида 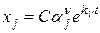 или в случае комплексного
или в случае комплексного 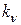 – его действительная (или мнимая) часть
– его действительная (или мнимая) часть 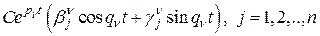 при сколь угодно малых по модулю
при сколь угодно малых по модулю 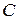 неограниченно возрастает по модулю при
неограниченно возрастает по модулю при 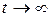 , т.е. точки, расположенные в начальный момент в
, т.е. точки, расположенные в начальный момент в 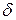 - окрестности начала координат при возрастании
- окрестности начала координат при возрастании  покидают любую заданную
покидают любую заданную 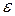 - окрестность начала координат, т.е. в этом случае точка покоя
- окрестность начала координат, т.е. в этом случае точка покоя 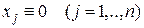 системы (3) неустойчива.
системы (3) неустойчива.
2. Теоремы Ляпунова об устойчивости.
Рассмотрим систему дифференциальных уравнений вида
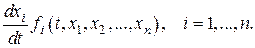 (4)
(4)
Теорема 1. Если существует дифференцируемая функция 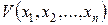 , называемая функцией Ляпунова, удовлетворяющая в окрестности начала координат условиям:
, называемая функцией Ляпунова, удовлетворяющая в окрестности начала координат условиям:
1) 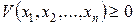 , причем
, причем 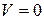 лишь при
лишь при 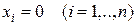 , т.е. функция
, т.е. функция 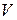 имеет строгий минимум в начале координат (положительно определенная функция).
имеет строгий минимум в начале координат (положительно определенная функция).
2) 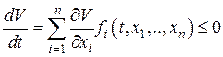 при
при 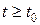 , то точка покоя
, то точка покоя 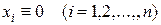 устойчива.
устойчива.
Производная в условии 2) взята вдоль интегральной кривой, т.е. в предположении, что аргументы 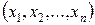 функции
функции 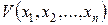 заменены решением
заменены решением 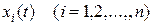 системы (4).
системы (4).
При этом
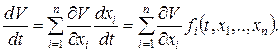
Доказательство. В окрестности начала координат как в окрестности точки строгого минимума поверхности уровня 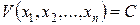 являются замкнутыми поверхностями, внутри которых находится точка минимума –
являются замкнутыми поверхностями, внутри которых находится точка минимума – 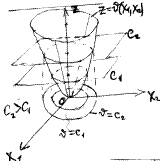 начало координат. Зададим
начало координат. Зададим 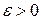 . При достаточно малом
. При достаточно малом 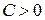 поверхность уровня
поверхность уровня 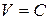 целиком лежит в
целиком лежит в 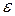 – окрестности начала координат (точнее, по крайней мере одна замкнутая компонента поверхности
– окрестности начала координат (точнее, по крайней мере одна замкнутая компонента поверхности 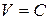 лежит в
лежит в 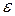 - окрестности начала координат), но не проходит через него, следовательно, можно выбрать такое
- окрестности начала координат), но не проходит через него, следовательно, можно выбрать такое 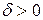 , что
, что 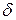 - окрестность начала координат целиком лежит внутри поверхности
- окрестность начала координат целиком лежит внутри поверхности 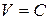 , причем в этой окрестности
, причем в этой окрестности 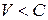 . Если начальная точка с координатами
. Если начальная точка с координатами 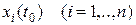 выбрана в
выбрана в 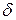 - окрестности начала координат, т.е.
- окрестности начала координат, т.е. 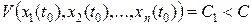 , то при
, то при 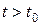 точка траектории, определяемой этими начальными условиями, не может выйти за пределы поверхности уровня
точка траектории, определяемой этими начальными условиями, не может выйти за пределы поверхности уровня 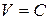 , т.к. в силу условия 2) теоремы, функция
, т.к. в силу условия 2) теоремы, функция 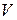 вдоль траектории не возрастает и, следовательно, при
вдоль траектории не возрастает и, следовательно, при 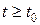
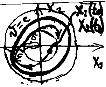
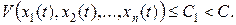
Что и требовалось доказать.
Теорема 2 (об асимптотической устойчивости). Если существует дифференцируемая функция Ляпунова 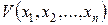 , удовлетворяющая в некоторой окрестности начала координат условиям:
, удовлетворяющая в некоторой окрестности начала координат условиям:
1) 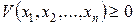 и имеет строгий минимум в начале координат:
и имеет строгий минимум в начале координат: 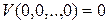 ;
;
2) производная функции 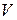 , вычисленная вдоль интегральной кривой системы (4)
, вычисленная вдоль интегральной кривой системы (4)
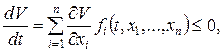
причем вне сколь угодно малой окрестности начала координат, т.е. при 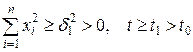 , производная
, производная 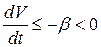 , где
, где 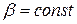 , то точка покоя
, то точка покоя 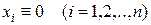 системы (4) асимптотически устойчива.
системы (4) асимптотически устойчива.
Доказательство. Так как условия теоремы 1 выполнены, то для любого 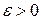 можно подобрать такое
можно подобрать такое 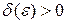 , что траектория, начальная точка которой находится в
, что траектория, начальная точка которой находится в 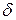 - окрестности начала координат при
- окрестности начала координат при 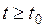 не выходит за пределы
не выходит за пределы 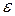 - окрестности начала координат. Следовательно, вдоль такой траектории при
- окрестности начала координат. Следовательно, вдоль такой траектории при 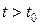 выполнено условие 2), поэтому вдоль траектории функция
выполнено условие 2), поэтому вдоль траектории функция 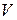 монотонно убывает с возрастанием
монотонно убывает с возрастанием  и ограничена снизу, и вдоль траектории существует предел функции
и ограничена снизу, и вдоль траектории существует предел функции 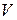 при
при 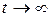 :
:
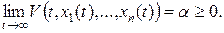
Если 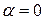 , то из условия 1) будет следовать, что
, то из условия 1) будет следовать, что 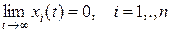 , т.е. точка покоя
, т.е. точка покоя 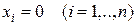 асимптотически устойчива.
асимптотически устойчива.
Допустим, что 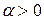 , тогда траектория при
, тогда траектория при 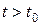 находится в области
находится в области 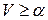 , следовательно, вне некоторой
, следовательно, вне некоторой 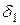 – окрестности начала координат, т.е. там, где по условию 2)
– окрестности начала координат, т.е. там, где по условию 2) 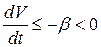 при
при 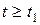 . Умножая неравенство
. Умножая неравенство 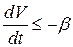 на
на 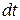 и, интегрируя вдоль траектории в пределах от
и, интегрируя вдоль траектории в пределах от 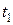 до
до  , получим
, получим
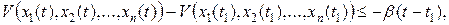
или
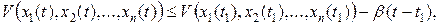
При достаточно большом  правая часть становится отрицательной, т.е.
правая часть становится отрицательной, т.е. 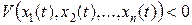 , что противоречит условию 1). Ч.т.д.
, что противоречит условию 1). Ч.т.д.
Теорема 3 (Четаева) о неустойчивости.
Если существует дифференцируемая функция 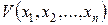 , удовлетворяющая в замкнутой
, удовлетворяющая в замкнутой 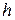 - окрестности начала координат следующим условиям:
- окрестности начала координат следующим условиям:
1) 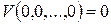 и в любой окрестности начала координат имеются точки, в которых
и в любой окрестности начала координат имеются точки, в которых 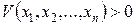 ;
;
2) 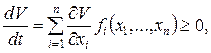 причем
причем 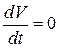 лишь при
лишь при 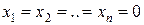 , то точка покоя
, то точка покоя 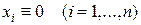 системы (4) неустойчива.
системы (4) неустойчива.
Доказательство. Начальную точку 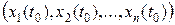 возьмем на том
возьмем на том 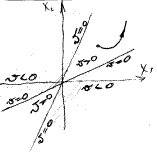 множестве, где
множестве, где 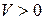 . Т.к. вдоль траектории
. Т.к. вдоль траектории 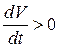 , то функция
, то функция 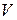 вдоль траектории возрастает. Допустим, что траектория не покидает
вдоль траектории возрастает. Допустим, что траектория не покидает 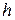 - окрестность начала координат. Тогда умножая неравенство
- окрестность начала координат. Тогда умножая неравенство 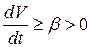 на
на 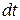 и интегрируя, имеем
и интегрируя, имеем
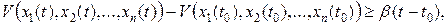
т.е. при 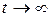 функция
функция 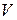 вдоль траектории неограниченно возрастает, что невозможно, т.к. дифференцируемая в замкнутой области функция
вдоль траектории неограниченно возрастает, что невозможно, т.к. дифференцируемая в замкнутой области функция 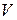 ограничена. Таким образом, траектория покидает
ограничена. Таким образом, траектория покидает 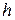 - окрестность точки покоя, т.е. точка покоя неустойчива. Ч.т.д.
- окрестность точки покоя, т.е. точка покоя неустойчива. Ч.т.д.
Общего метода построения функции Ляпунова не существует. Часто её можно построить в виде квадратичной формы 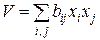 .
.
Пример 1.
Исследовать на устойчивость тривиальное решение системы
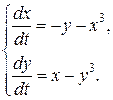
Рассмотрим функцию 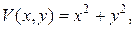 она удовлетворяет условиям теоремы Ляпунова:
она удовлетворяет условиям теоремы Ляпунова:
1) 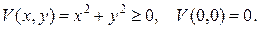
2) 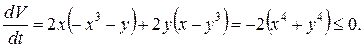
Решение устойчиво.
Вне окрестности начала координат
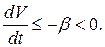
Следовательно, решение 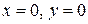 асимптотически устойчиво.
асимптотически устойчиво.
Пример 2.
Исследовать на устойчивость точку покоя системы.
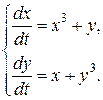
Функция 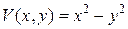 удовлетворяет условиям теоремы Четаева:
удовлетворяет условиям теоремы Четаева:
1) 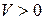 при
при 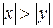 ; 2)
; 2) 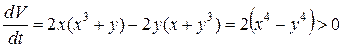 при
при 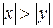 , причем при
, причем при 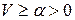 ,
, 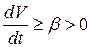 . Следовательно, точка покоя
. Следовательно, точка покоя 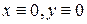 неустойчива.
неустойчива.
3. Исследование на устойчивость по первому приближению.
Рассмотрим нелинейную нормальную систему дифференциальных уравнений
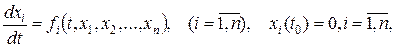 (1)
(1)
где 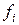 – дифференцируемые в окрестности начала координат
– дифференцируемые в окрестности начала координат 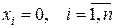 функции.
функции.
Напомним, что исследование на устойчивость точки покоя 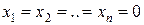 системы (1) эквивалентно исследованию на устойчивость некоторого решения
системы (1) эквивалентно исследованию на устойчивость некоторого решения 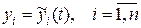 системы дифференциальных уравнений
системы дифференциальных уравнений
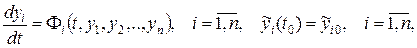 (2)
(2)
т.к. система (1) может быть получена из (2) после замены
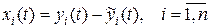
в результате, которой из (2) имеем
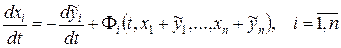 (3)
(3)
Обозначив правую часть в (3) через 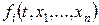 получим систему (1). Из (3) и (2) видно, что в точке покоя, т.е. при
получим систему (1). Из (3) и (2) видно, что в точке покоя, т.е. при 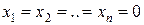 правые части системы (1) обращаются в нуль:
правые части системы (1) обращаются в нуль: 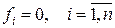 , т.е.
, т.е. 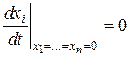 - это точка покоя.
- это точка покоя.
Теперь, с учетом этого обстоятельства и пользуясь дифференцируемостью функций 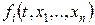 , представим систему (1) в окрестности начала координат
, представим систему (1) в окрестности начала координат 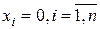 в следующем виде
в следующем виде
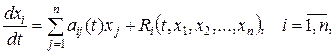 (4)
(4)
где 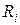 имеют порядок выше первого относительно
имеют порядок выше первого относительно 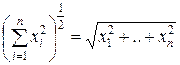 .
.
Будем исследовать на устойчивость точку покоя 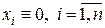 линейной системы
линейной системы
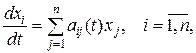 (5)
(5)
называемой системой уравнений первого приближения для системы (4).
Если все коэффициенты 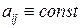 , т.е. система (1) стационарна в первом приближении, то исследование на устойчивость линейной системы (5) не представляет принципиальных затруднений (см.раздел 1.3). В отношении системы (4) имеют место следующие теоремы.
, т.е. система (1) стационарна в первом приближении, то исследование на устойчивость линейной системы (5) не представляет принципиальных затруднений (см.раздел 1.3). В отношении системы (4) имеют место следующие теоремы.
Теорема 1. Если система уравнений (4) стационарна в первом приближении, все члены 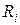 в достаточно малой окрестности начала координат (при
в достаточно малой окрестности начала координат (при 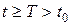 ) удовлетворяет неравенствам
) удовлетворяет неравенствам 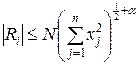 , где
, где 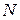 и
и 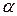 - постоянные, причем
- постоянные, причем 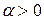 и все корни характеристического уравнения
и все корни характеристического уравнения
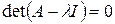 (6)
(6)
имеют отрицательные действительные части, то тривиальное решение 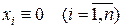 системы (4) и системы уравнений (5) асимптотически устойчивы, следовательно, в этом случае возможно исследование на устойчивость по первому приближению.
системы (4) и системы уравнений (5) асимптотически устойчивы, следовательно, в этом случае возможно исследование на устойчивость по первому приближению.
Теорема 2. Если система уравнений (4) стационарна в I приближении, все функции 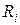 удовлетворяют условиям предыдущей теоремы, и хотя бы один корень характеристического уравнения (6) имеет положительную действительную часть, то точки покоя
удовлетворяют условиям предыдущей теоремы, и хотя бы один корень характеристического уравнения (6) имеет положительную действительную часть, то точки покоя 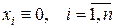 системы (4) и системы (5) неустойчивы, следовательно, и в этом случае возможно исследование на устойчивость по I приближению
системы (4) и системы (5) неустойчивы, следовательно, и в этом случае возможно исследование на устойчивость по I приближению
В так называемом критическом случае, когда все действительные части корней характеристического уравнения неположительны, причем действительная часть хотя бы одного корня равна нулю, на устойчивость тривиального решения системы (4) начинают влиять нелинейные члены 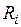 , и исследование на устойчивость по первому приближению, вообще говоря, невозможно.
, и исследование на устойчивость по первому приближению, вообще говоря, невозможно.
Докажем теорему 1 в предположении, что все корни 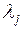 характеристического уравнения (6) действительны и различны
характеристического уравнения (6) действительны и различны
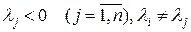 при
при 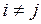 .
.
В векторных обозначениях системы (4) и (5) примут соответственно следующий вид
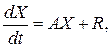 (4а)
(4а)
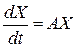 , (5а)
, (5а)
где
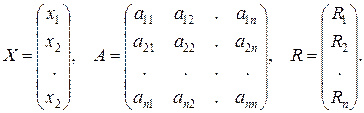
С помощью невырожденного линейного преобразования с постоянными коэффициентами 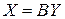 , где
, где
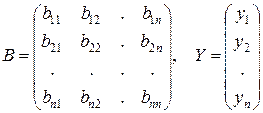
преобразуем систему (5а) к виду
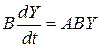 или
или 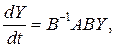
в котором матрица 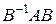 диагональна
диагональна
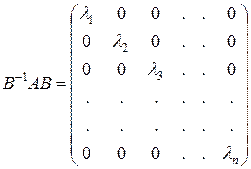 ,
,
т.е. система (5) примет вид
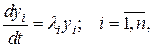
а система (4) при том же преобразовании переходит в
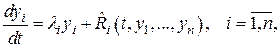 (7)
(7)
где 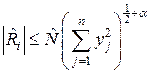 ,
, 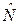 - постоянная величина,
- постоянная величина, 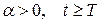 (т.к.
(т.к. 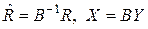 ).
).
Для системы (7) функцией Ляпунова, удовлетворяющей условиям теоремы об асимптотической устойчивости, является
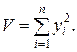
Действительно,
1) 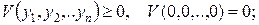
2) 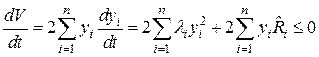
при достаточно малых 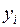 , т.к. все
, т.к. все 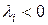 , а величина
, а величина 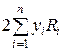 при достаточно малых
при достаточно малых 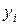 может быть сделана по модулю меньше суммы
может быть сделана по модулю меньше суммы 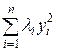 .
.
Наконец, вне некоторой окрестности начала координат 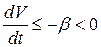 . Таким образом, система (7), а, следовательно, и (4), как и система (5), асимптотически устойчива. Ч.т.д.
. Таким образом, система (7), а, следовательно, и (4), как и система (5), асимптотически устойчива. Ч.т.д.
Пример 1.
Исследовать на устойчивость точку покоя 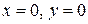 системы
системы
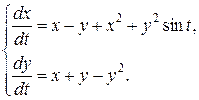 (8)
(8)
Здесь 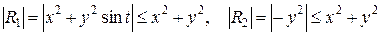 , т.е.
, т.е. 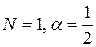 . Удовлетворяются условию теорем 1 и 2. Поэтому исследуем на устойчивость точку покоя
. Удовлетворяются условию теорем 1 и 2. Поэтому исследуем на устойчивость точку покоя 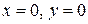 системы первого приближения.
системы первого приближения.
