Часть 2: производная и ее применение к исследованию функций. асимптоты графика функции

Лекция 9

Асимптоты графика функции. Построение эскиза графика функции

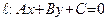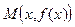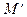Пусть даны функция , прямая , точка на графике функции и обозначим через проекцию точки M на прямую .

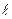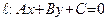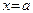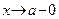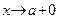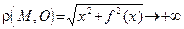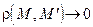Определение 18. Прямая называется левосторонней (соответственно, правосторонней) асимптотой графика функции в точке (a может принимать и бесконечные значения), если при (соотв. при ) , а (где 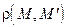– расстояние между точками M и ).

€

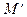Известно (см. ЛЛААГ), что уравнение прямой 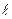можно записать либо в виде 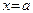, либо в виде .

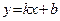Теорема 19. Прямая 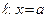(здесь a – конечное число) является левосторонней (соотв., правосторонней) асимптотой графика функции в точке 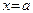тогда и только тогда, когда

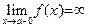(соотв, ).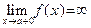

(28)

Доказательство. Проведем доказательство только для левосторонних асимптот.

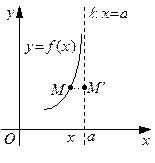Пусть 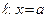– левосторонняя асимптота. Применяя определение 18, получаем:

.

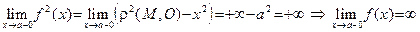Обратно, пусть 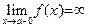.Тогда ясно, что 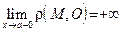и 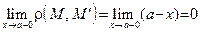, то есть по определению 18 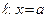– левосторонняя асимптота.

€

Заметим, что прямая 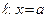не может быть асимптотой графика функции ни в одной другой точке 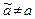(докажите это!). Асимптоты вида 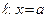часто называют вертикальными асимптотами.

Следствие. График функции, непрерывной на всей числовой прямой, не имеет вертикальных асимптот. œ

Теорема 20. 1)Если прямая 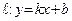является левосторонней (соотв., правосторонней) асимптотой графика функции на бесконечности, то

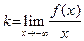(соотв., )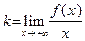

(29)

и

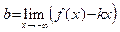(соотв., ).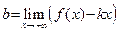

(30)

2) Если пределы (29) и (30) существуют и конечны, то прямая 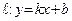является левосторонней (соотв., правосторонней) асимптотой графика функции на бесконечности.

Доказательство. Доказательство проведем только для правосторонней асимптоты.

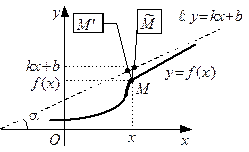1) Пусть 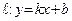– правосторонняя асимптота графика функции (см. рисунок). Имеем: ,

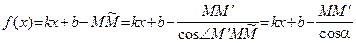где 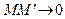при 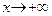(см. определение 18). Следовательно, 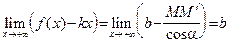, что доказывает равенство (30). Теперь (29) следует из (30):

.

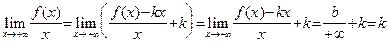2) Обратно, пусть пределы (29) и (30) существуют и конечны. Опять из соотношения 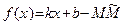получаем: 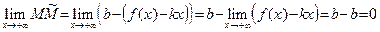. Так как 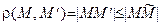, то 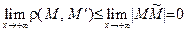, то есть 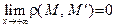. Соотношение 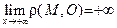очевидно. Таким образом, 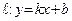– правосторонняя асимптота графика функции на бесконечности.

€

Заметим, что прямая 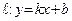не может быть асимптотой графика функции ни в одной точке 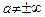(докажите это!). Асимптоты вида 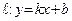часто называют наклонными асимптотами. В частности, если 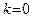, то такие асимптоты называют горизонтальными.

Теорема 21. Пусть – рациональная дробь, то есть

,
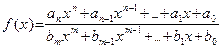где 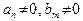, причем числитель и знаменатель не имеют одинаковых действительных корней. Тогда:

1) если 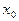– действительный корень знаменателя дроби, то 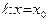– вертикальная асимптота графика функции ;

2) график функции имеет наклонные асимптоты тогда и только тогда, когда 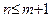; при этом наклонные асимптоты в точках 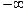и 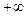совпадают.

Доказательство. Доказательство пункта 1) просто и предоставляется читателю. Докажем 2). Применяя теорему 6, имеем:

.

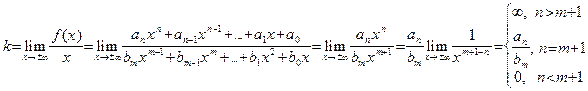(31)

Если 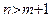, то по теореме 20 асимптот нет. Если 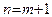, то

,
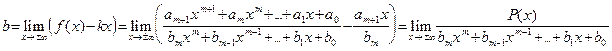где степень многочлена P(x) не превосходит m (докажите это!). Опять применяя теорему 6, получаем конечность числа b.

Если 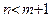, то 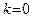, и конечность числа 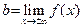снова следует из теоремы 6.

€

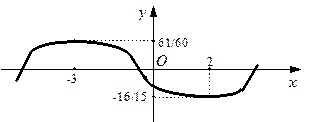Пример 26 (продолжение примера 21). Так как многочлен 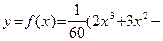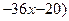непрерывен на всей числовой прямой, то по следствию из теоремы 19 график этой функции не имеет вертикальных асимптот. Наклонных асимптот также нет, так как здесь 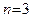, а 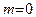(см. п. 2) теоремы 21). Построим эскиз графика данной функции. Начинаем построение с кусков графиков в окрестностях критических точек (см. таблицу в примере 21), а затем соединяем эти куски так, чтобы получилась непрерывная кривая. Уточнение этого графика будет произведено с помощью исследования второй производной. ›

Пример 27 (продолжение примера 22). По теореме 21 рациональная дробь 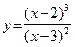имеет вертикальную асимптоту 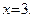По той же теореме, так как 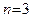, а 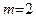, данная функция имеет двухстороннюю наклонную асимптоту. По формуле (31) 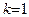. Найдем b:

.

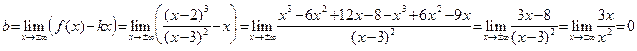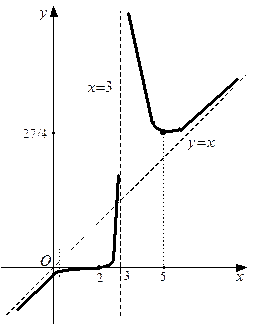Итак, наклонная асимптота задается уравнением .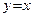

Построение эскиза графика начинаем с критических точек и асимптот, которые будем наносить штриховыми линиями. Если x приближается к 3, то соответствующие точки графика функции уходят вверх (см. данные таблицы в примере 22 о поведении функции на интервалах 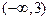и 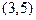). Ес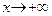ли или 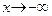, то соответствующие точки графика приближаются к наклонной асимптоте 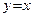. Если рассуждать априорно, то в принципе соответствующие ветви графика могут приближаться к асимптоте и с другой стороны. Точно ответить на этот вопрос мы сможем после нахождения точек перегиба и интервалов выпуклости.

€

Пример 28 (продолжение примера 23). Очевидно, график функции 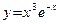не имеет вертикальных асимптот. Исследуем наличие наклонных асимптот. Принимая во внимание равенство (16), получаем:

,

.

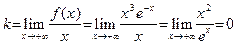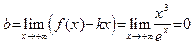Итак, мы получили правостороннюю горизонтальную асимптоту 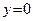. Посмотрим, есть ли левосторонняя наклонная асимптота. Имеем: 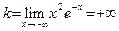. Согласно теореме 20, левосторонней наклонной асимптоты нет.

€

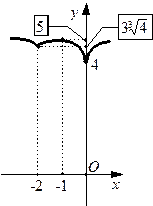Пример 29 (продолжение примера 24). Очевидно, график функции 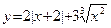не имеет вертикальных асимптот. Проведем исследование на наличие наклонных асимптот. Применяя выражение функции при 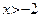, получаем: 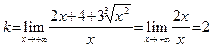, однако 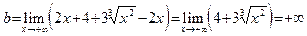. Следовательно, правосторонней наклонной асимптоты нет. Аналогично доказывается, что и левосторонней наклонной асимптоты также нет (проделайте это!).

€

Пример 30 (продолжение примера 25). Функция 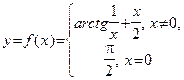имеет одну точку разрыва: 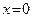. Однако в этой точке график данной функции не имеет вертикальной асимптоты, так как (см. вычисления в примере 25) оба предела 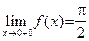и 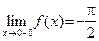конечны. Посмотрим, есть ли наклонные асимптоты. Имеем:

, .

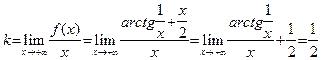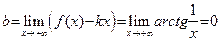По теореме 20 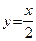– правосторонняя наклонная асимптота. Легко видеть, что эта асимптота является и левосторонней.

	€
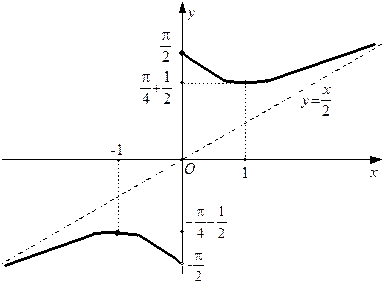