Лекция 5. Ряды Тейлора и Маклорена

5.1. Ряды Тейлора и Маклорена. Условия сходимости
рядов Тейлора к исходной функции

Пусть функция 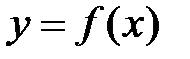определена в некоторой окрестности точки х₀: 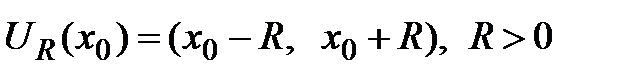и имеет производные любого порядка,
тогда для этой функции формально можно составить ряд по степеням :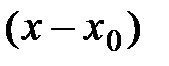

,
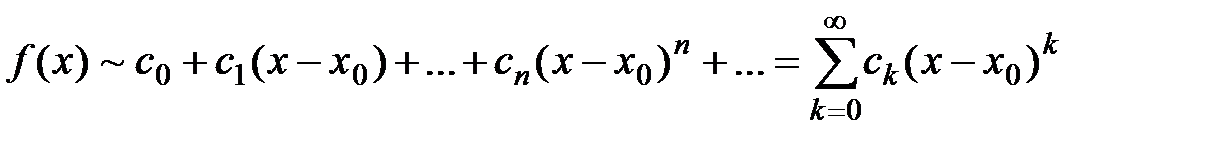где .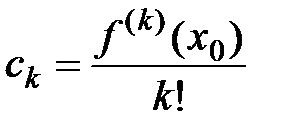

Определение 1. Обобщённый степенной ряд вида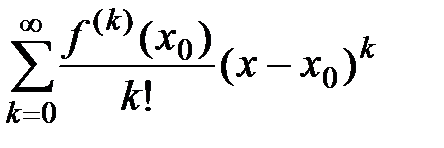
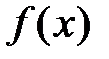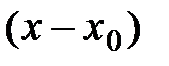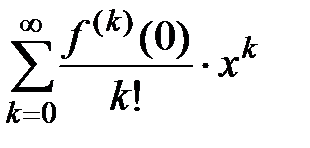называется рядом Тейлора для функции по степеням . Если положить , то получим ряд , который носит название ряда Маклорена для функции 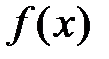по степеням х.

Задача. Пусть задана функция 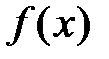, бесконечно дифференцируемая в окрестности точки х₀: 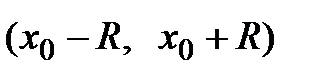, и пусть для этой функции составлен ряд Тейлора по степеням 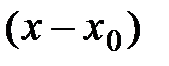: 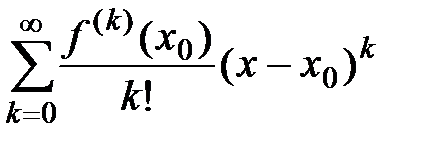и его сумма равна 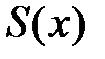. Если интервал 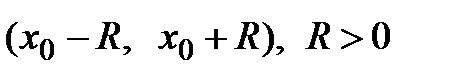является интервалом сходимости данного ряда с радиусом сходимости R, то можно записать равенство:

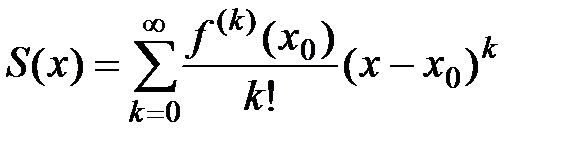
при всех .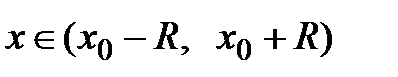

Выясним, при каких условиях такой степенной ряд имеет своей суммой функцию 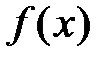, т.е. когда 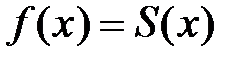, поскольку существуют функции, для которых сумма ряда Тейлора не совпадает с данной функцией.

Рассмотрим пример. Дана функция 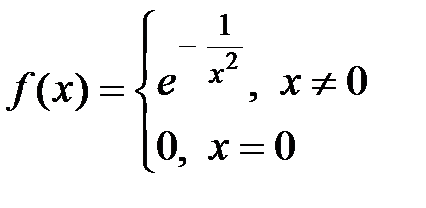, которая является бесконечно дифференцируемой . Вычислим производные этой функции в точке : 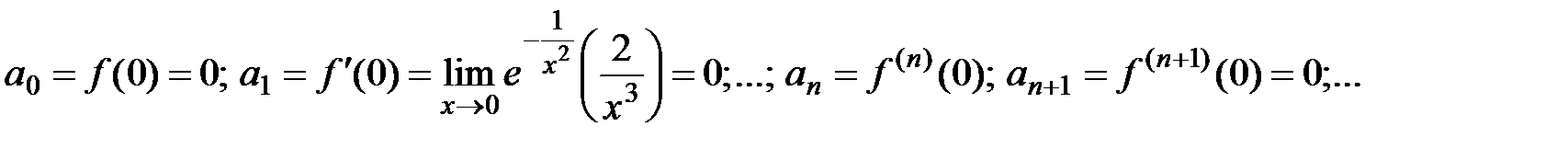Таким образом, все вычисленные коэффициенты ряда Тейлора–Маклорена для данной функции равны 0, поэтому этот ряд сходится на всей оси, его сумма тождественно равна 0: 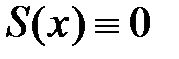, однако 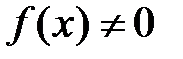при 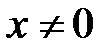( 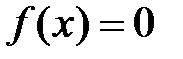только в начале координат).

Пусть ряд Тейлора 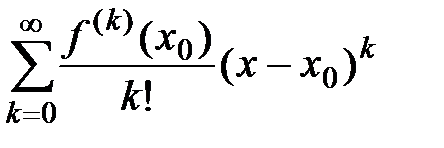имеет интервал сходимости 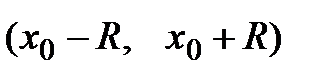, где R – радиус сходимости. Тогда, если 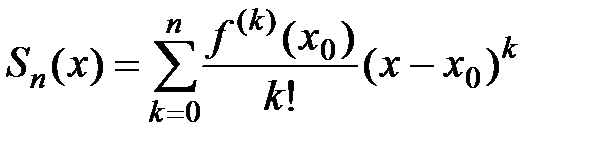− частичная сумма этого ряда, то для любого 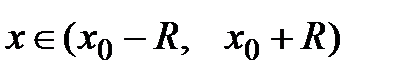существует 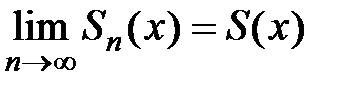. Рассмотрим теорему, которая даёт условия того, что .

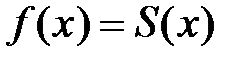Теорема 1 (необходимый и достаточный признак сходимости ряда Тейлора к функции f(x)). Для того чтобы ряд Тейлора 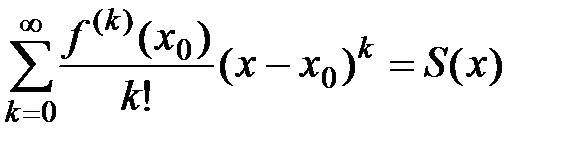, , 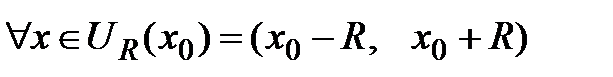имел своей суммой функцию 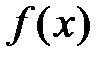, т.е. 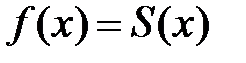, необходимо и достаточно, чтобы

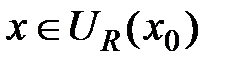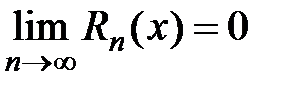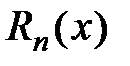для всех существовал предел , где − остаток ряда Тейлора.

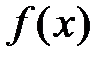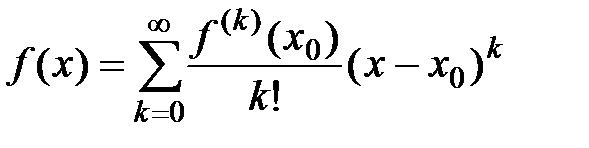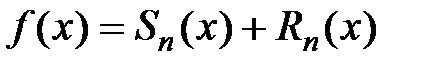Доказательство. 1) Необходимость. Пусть функция есть сумма ряда Тейлора на указанном промежутке: , или , где 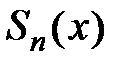− частичная сумма ряда Тейлора, 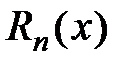− остаток ряда Тейлора. Из условия сходимости ряда 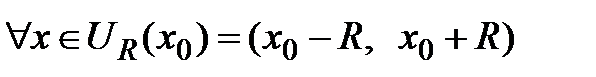существует предел 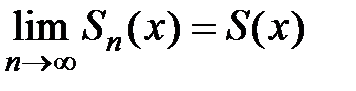, и так как 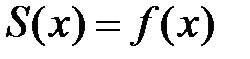, то существует предел

,

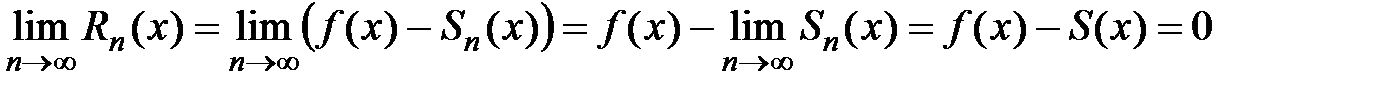т.е. 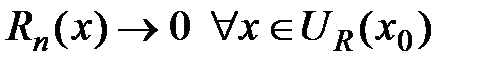. Необходимость доказана.

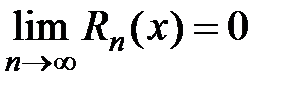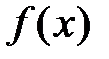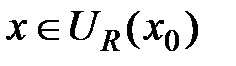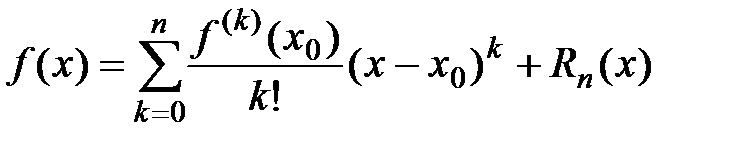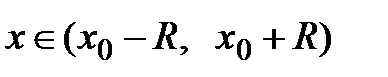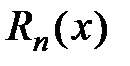2) Достаточность. Пусть существует . Так как функция бесконечно дифференцируема при всех , то для неё имеет место формула Тейлора для всех , где − остаточный член формулы Тейлора, который совпадает с остатком ряда Тейлора. Тогда частичная сумма соответствующего ряда Тейлора имеет вид:

.

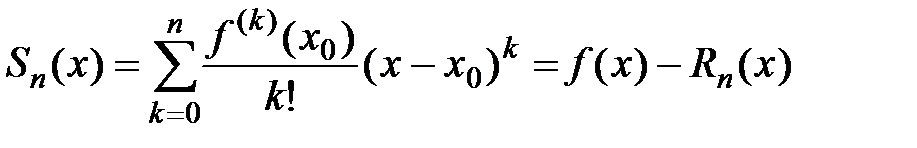Рассмотрим предел 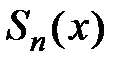, который обозначим через 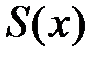, учитывая, что 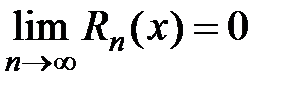: 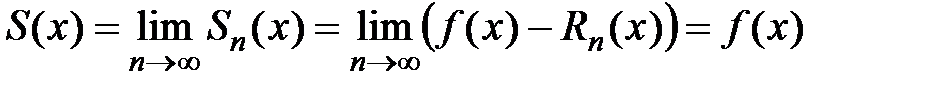, т.е. 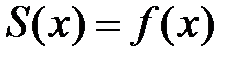. Достаточность доказана.

Замечание. Если 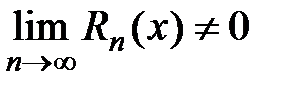, то сумма ряда Тейлора может не совпадать

с данной функцией, т.е. 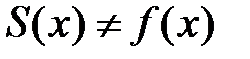, хотя сам ряд может сходиться к другой функции.

Необходимое и достаточное условие сходимости ряда Тейлора к
исходной функции неудобно для проверки на практике конкретных рядов; существуют более простые, хотя и более жёсткие, достаточные условия разложения функции 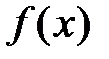в ряды Тейлора−Маклорена. Сначала сформулируем лемму.

Лемма. Для любого R существует следующий предел: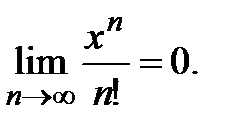

Доказательство. Рассмотрим степенной ряд 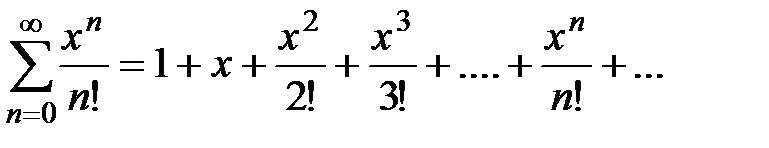, общий член которого 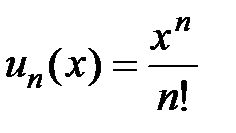. Найдём радиус и область сходимости этого ряда, используя признак
Даламбера. Вычисляем предел, учитывая, что :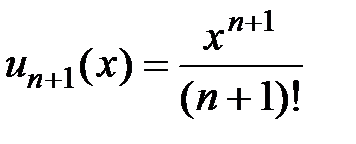

,

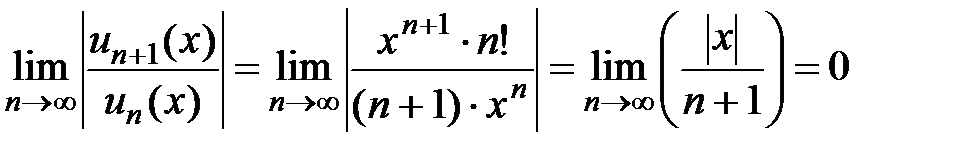т.е. радиус сходимости ряда 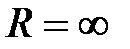. Следовательно, рассмотренный ряд сходится для всех 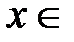R, тогда по необходимому признаку сходимости общий член ряда 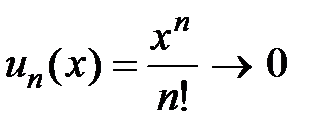, , 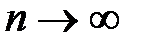т.е. 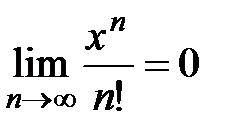для любого

R.

Теорема 2 (достаточные условия разложимости функции f(x) в ряд Маклорена). Пусть функция определена и бесконечно дифференцируема на интервале 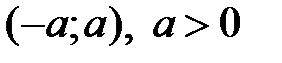. Если существует такое число 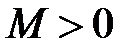, что для каждого натурального 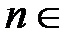N и всех 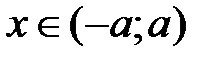выполняется неравенство: 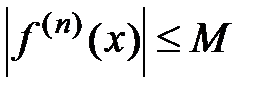(это означает, что производные любого порядка ограничены одним и тем же числом), тогда остаток ряда Маклорена 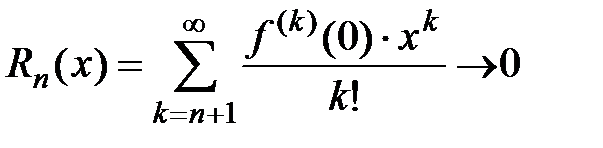при 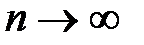, а значит, .

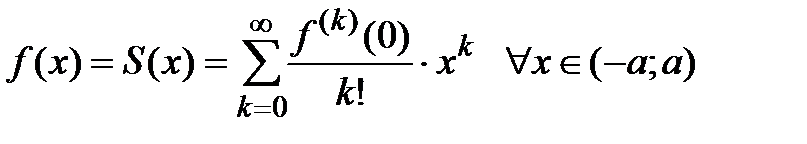Доказательство. Покажем, что остаток ряда Маклорена стремится к нулю при 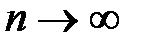. Запишем для функции 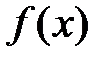формулу Маклорена с остаточным членом в форме Лагранжа: 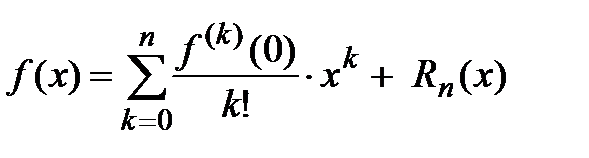, где 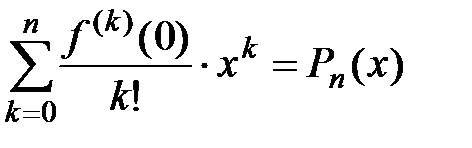− многочлен Маклорена, а 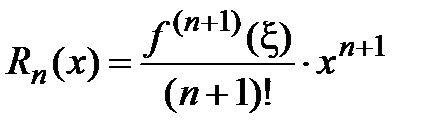. Отметим, что частичная сумма ряда Маклорена 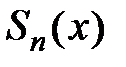совпадает с многочленом Маклорена 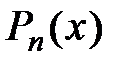, а остаток ряда есть 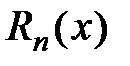. Выполним его оценку, используя условия теоремы 2 и учитывая, что 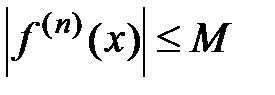для всех :

.
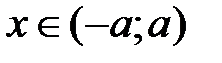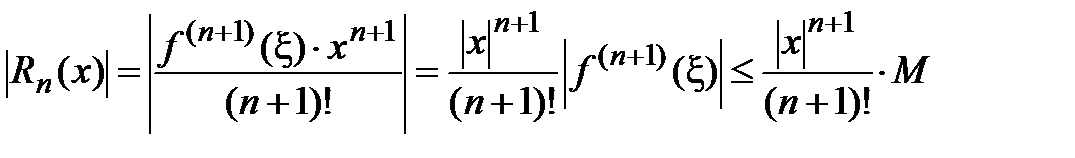По лемме 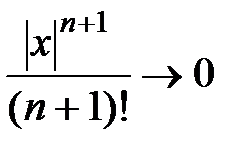при 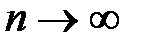, тогда , .
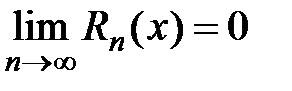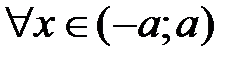Следовательно, по теореме 1 о необходимом и достаточном признаке сходимости ряда Тейлора к исходной функции получаем 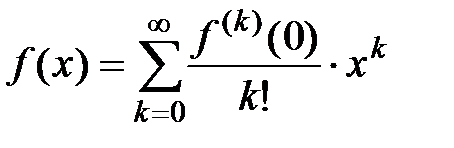. Теорема доказана.

5.2. Разложение основных элементарных функций в степенные ряды

Используем изложенную выше теорию для разложения основных элементарных функций в степенные ряды. Для разложения функции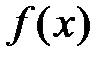

в степенной ряд по степеням 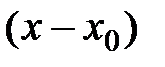можно рекомендовать следующий

порядок действий:

1) Находим производные функции 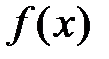в точке :

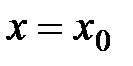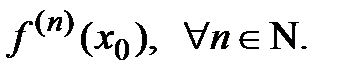
2) Составляем ряд Тейлора .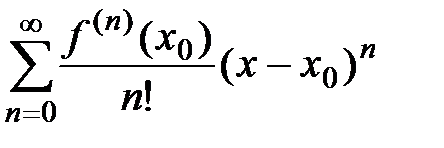

3) Находим интервал сходимости данного ряда: 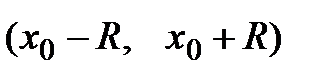, где R– радиус сходимости.

4) Исследуем поведение остатка ряда 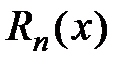для всех

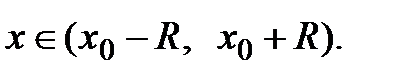
Если окажется, что 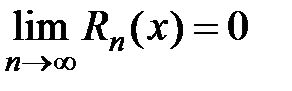, то на основании теорем 1 и 2 делаем вывод, что 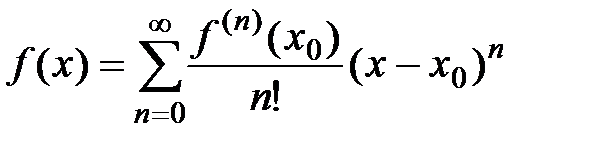при всех .
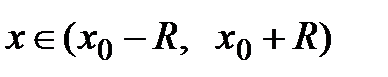В результате получаем формулу разложения функции в степенной ряд.

· Разложение в степенной ряд функции 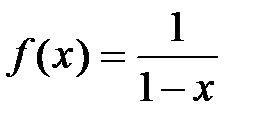имеет вид:

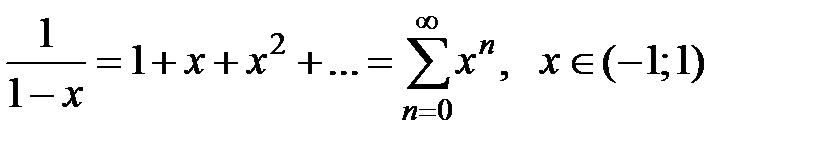(1)

Вывод. Рассмотрим ряд геометрической прогрессии 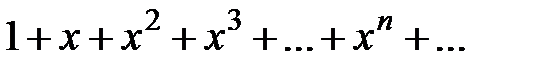, знаменатель которо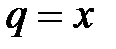й и 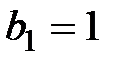. Можно показать, что интервал сходимости этого ряда 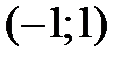, 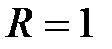и сумма этого ряда 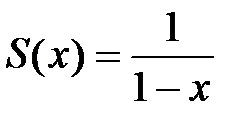(сумма ряда бесконечно убывающей геометрической прогрессии вычисляется по формуле 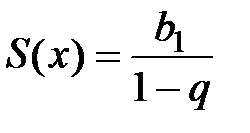). Оценим остаток ряда:

.

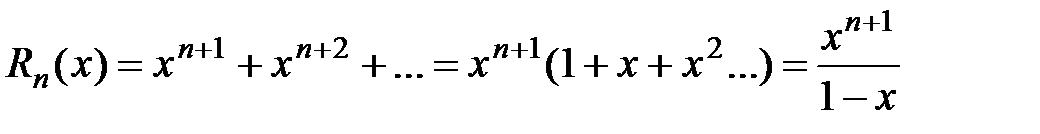При 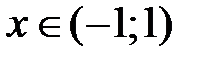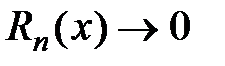, , 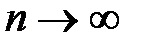тогда на основании теоремы 1

рассмотренный ряд имеет своей суммой функцию .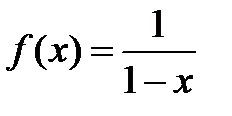

Разложение (1) имеет место.

· Разложение в степенной ряд функции 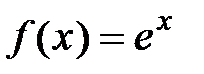имеет вид:

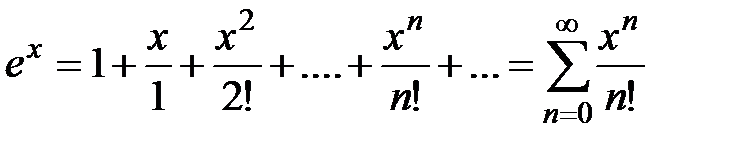, R (2)

Вывод. Для данной функции 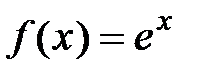запишем ряд Маклорена: 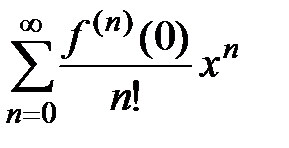. Так как функция 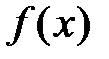− бесконечно дифференцируема, то все производные существуют и равны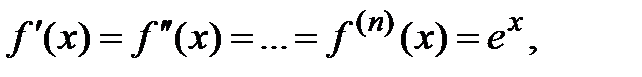

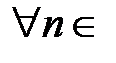N.

Находим эти производные в точке 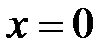; получаем 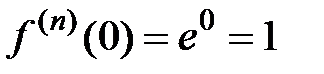для всех 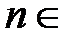N, тогда ряд Маклорена приобретает вид:

.

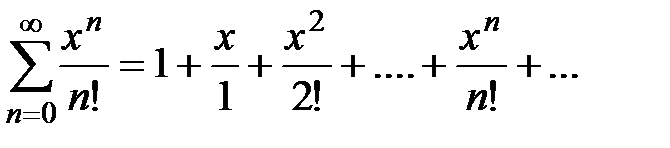Этот ряд сходится для всех 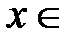R. Покажем, что сумма этого ряда равна 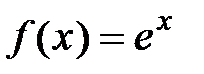. Фиксируем некоторое число 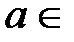R и рассмотрим некоторый отрезок [−a; a], на котором 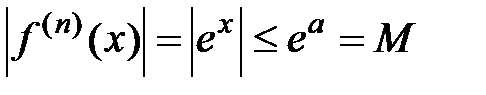для любого 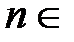N. В этом случае по теореме 2 данный ряд Маклорена будет сходиться на указанном отрезке к исходной функции 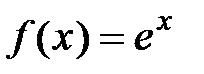. Отметим, что это верно для любого фиксированного числа 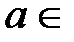R. Разложение (2) имеет место при всех 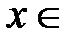R.

· Разложение в степенной ряд функции 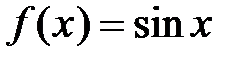имеет вид:

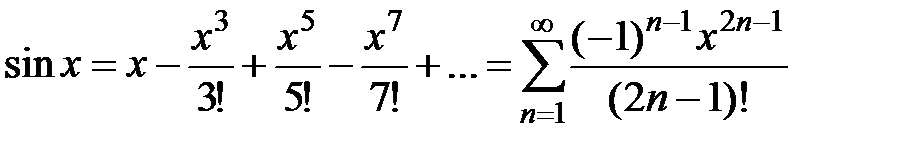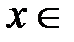, R (3)

Вывод. Для функции 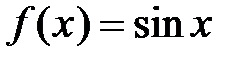запишем ряд Маклорена .

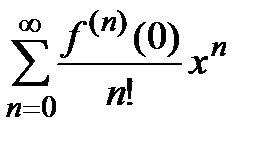Находим все производные: 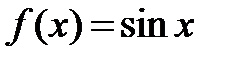, , 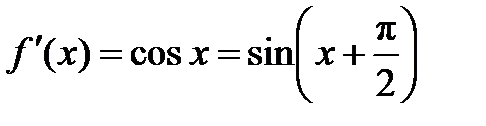, , 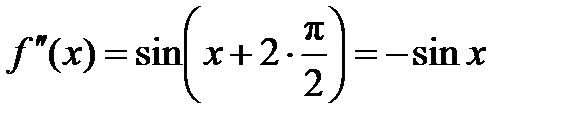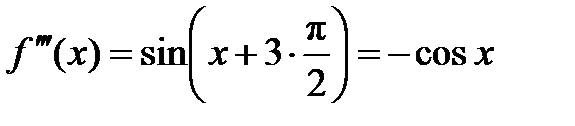…, 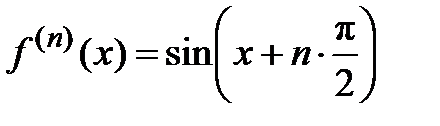. Вычисляем эти производные в точке х = 0:

.

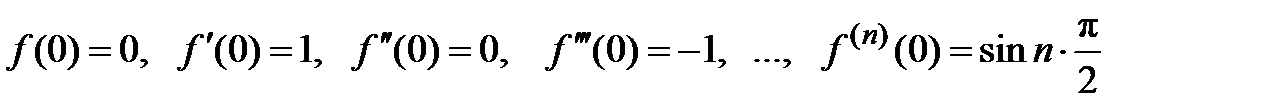Подставив эти значения в ряд Маклорена, получаем ряд:

.

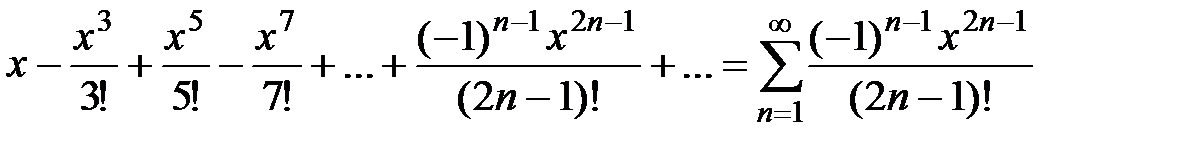Данный ряд сходится при любом 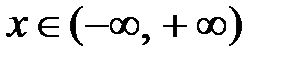; покажем, что он сходится к функции 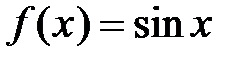. Согласно теореме 2 (поскольку 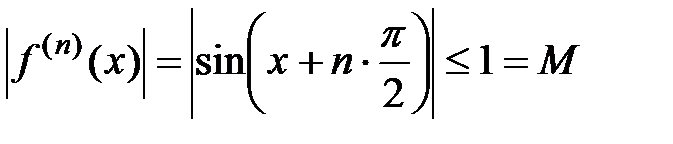, т.е. все производные ограничены одним и тем же числом) данный ряд Маклорена будет сходиться к исходной функции 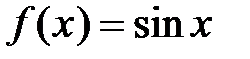при всех R. Таким образом разложение (3) имеет место.

· Разложение в степенной ряд функции 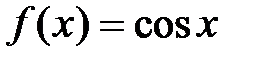имеет вид:

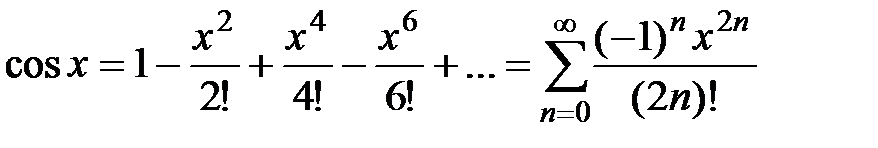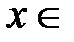, R (4)

Вывод. Рассмотрим разложение (3)

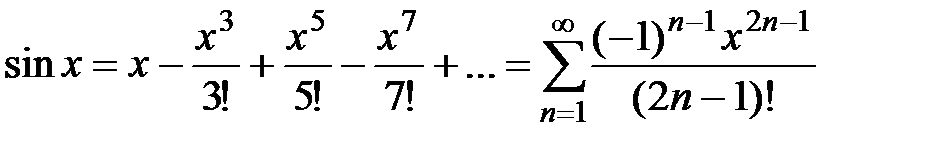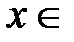, R. Продифференцируем данный степенной ряд; получившийся новый ряд будет также сходиться при всех 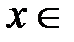R к функции, которая равна производной от 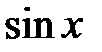(свойство 3, лекция 4, разд. 4.3), т.е.

.
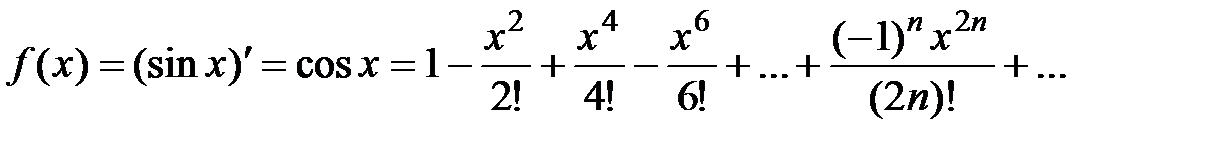Таким образом, разложение (4) имеет место.

· Разложение в степенной ряд функции 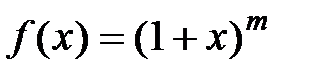имеет вид:

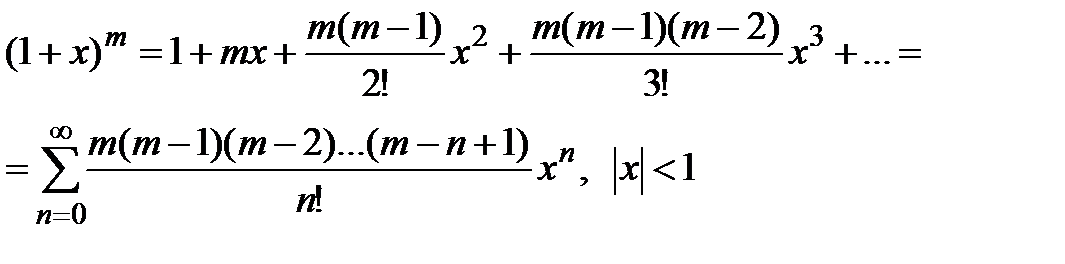(5)

Разложение (5) приводится без вывода. Отметим, что оно верно при фиксированном 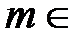R и называется биномиальным рядом.
При натуральном 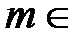N этот ряд представляет собой конечную сумму, известную как бином Ньютона:

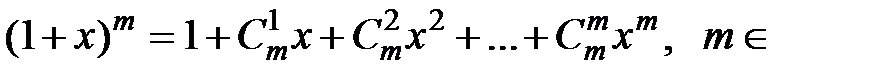N.
Для нецелых m имеет место формула Тейлора:

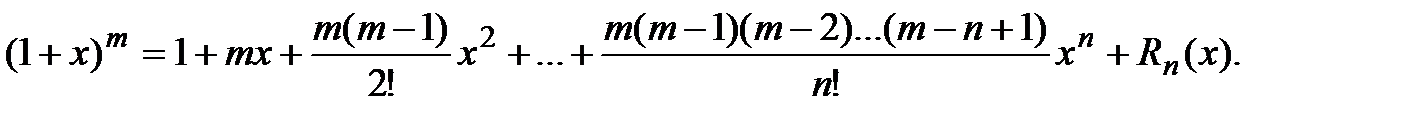
При 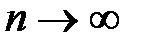из этой формулы получаем бесконечный степенной ряд (5). Найдём радиус его сходимости, применяя признак Даламбера. Учитывая, что 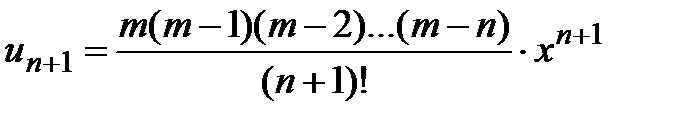, , 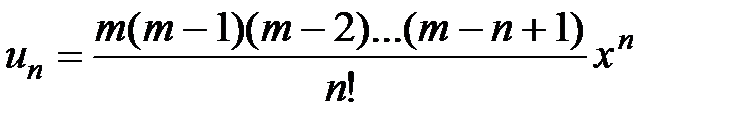вычисляем предел:

,

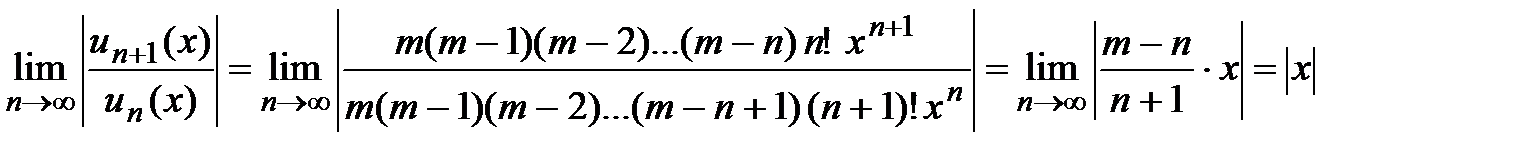тогда при 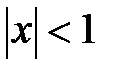ряд сходится и его радиус сходимости 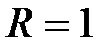, а интервал сходимости (−1;1) ; можно показать, что , .
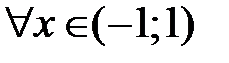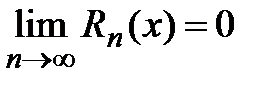Итак, разложение (5) верно для всех 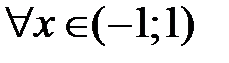. В частном случае, когда 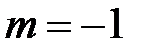, из разложения (5) получаем ряд :

,

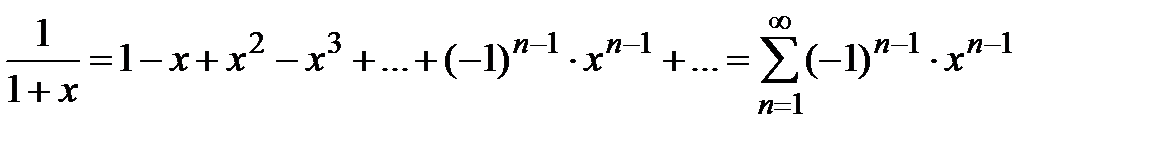который при 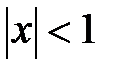абсолютно сходится. Если в каждом члене ряда заменить х на (− х), то получим разложение (1):

.

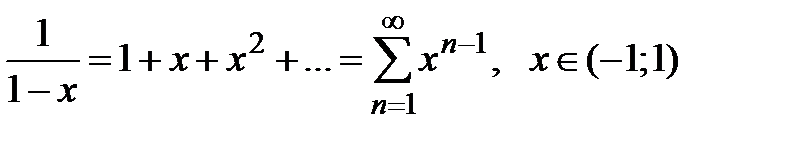· Разложение в степенной ряд функции 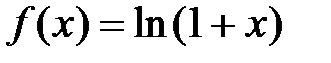имеет вид:

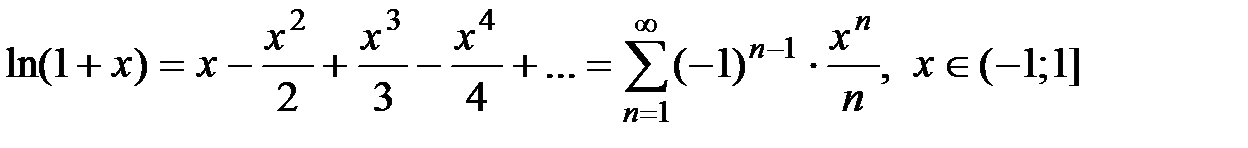(6)

Вывод. Из разложения (5) биномиального ряда при 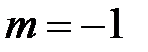получаем ряд геометрической прогрессии со знаменателем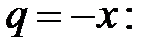

,

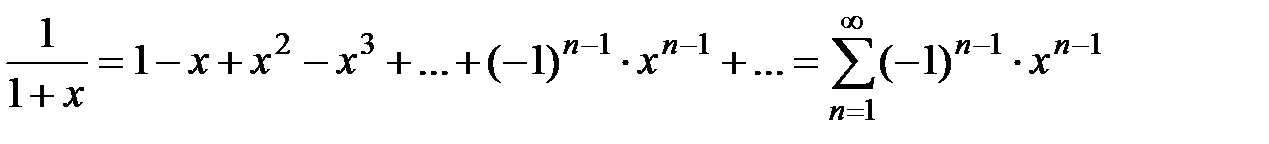который сходится при 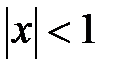, т.е. этот ряд имеет интервал сходимости (−1;1) с радиусом сходимости .

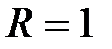Полученный ряд почленно интегрируем на отрезке 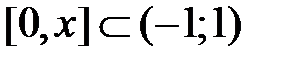, используя свойство 3 (лекция 4, разд. 4.3); при этом интервал сходимости сохранится:

.

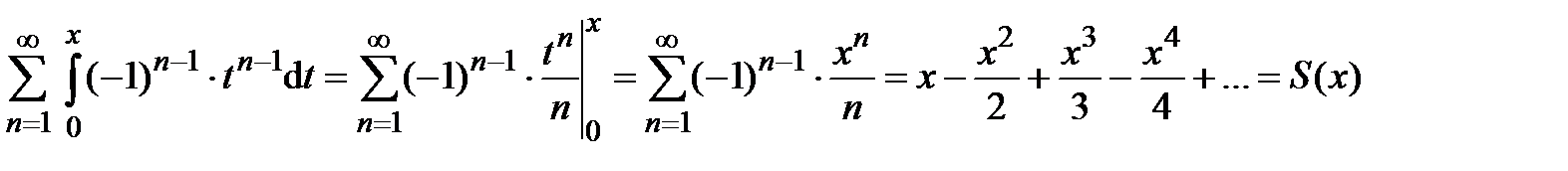Сумма полученного ряда равна

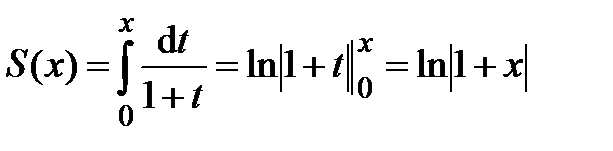
(или 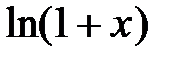, так как ).

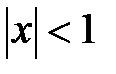Таким образом, 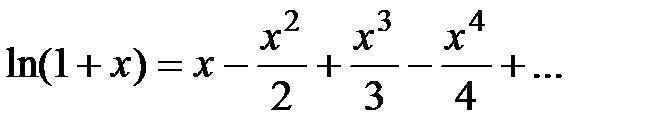, т.е. имеет место разложение (6) при 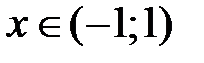. Исследуя сходимость данного ряда в точке 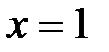, получаем числовой ряд 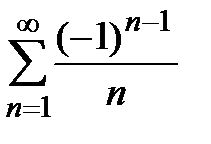, который условно сходится. Таким образом, область сходимости ряда в разложении (6) имеет вид 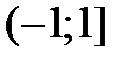, а радиус сходимости .

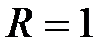· Разложение в степенной ряд функции 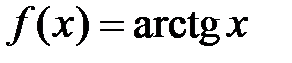имеет вид:

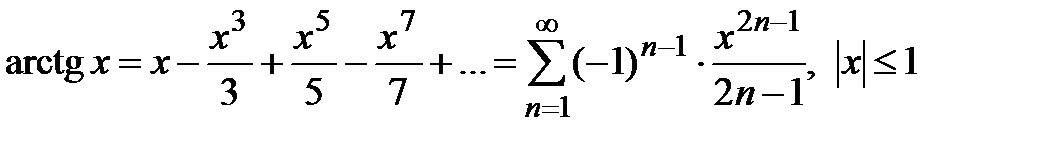(7)

Вывод. Из разложения (5) биномиального ряда при 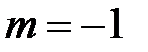получаем
разложение

,

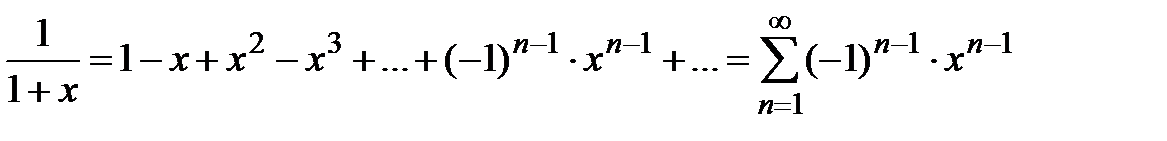из которого заменой 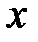на 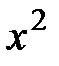вытекает следующий ряд:

,

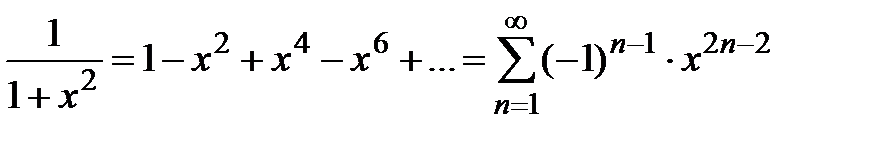сходящийся при 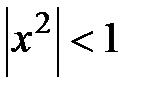, а именно, при 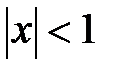. Полученный ряд почленно интегрируем на отрезке 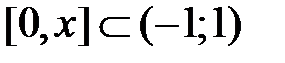, используя свойство 3 (лекция 4, разд. 4.3); при этом интервал сходимости сохранится, обозначим :

.

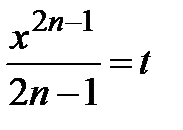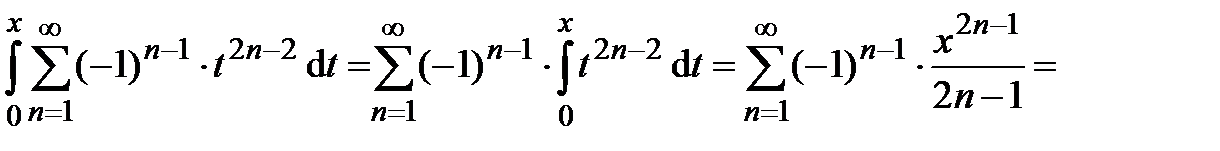
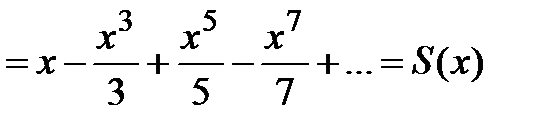Сумма полученного ряда

.

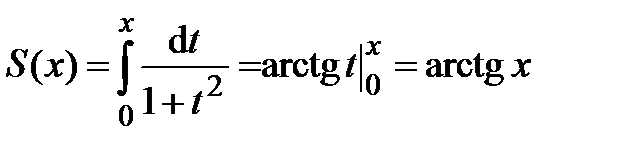Таким образом, 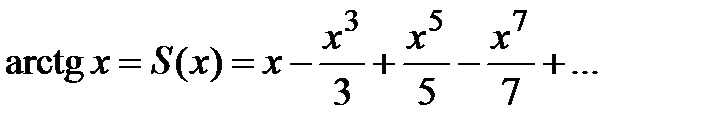, т.е. разложение (7)

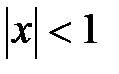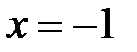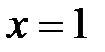имеет место при . Исследуя разложение (7) в точках и , получаем два условно сходящихся числовых ряда 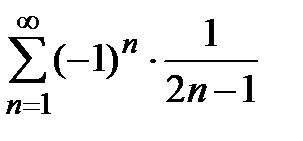и 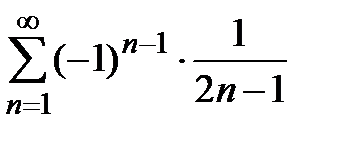соответственно. Таким образом, область сходимости ряда (7) является отрезком 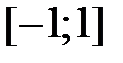, а радиус сходимости R равен 1.

· Разложение в степенной ряд функции 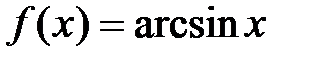имеет вид:

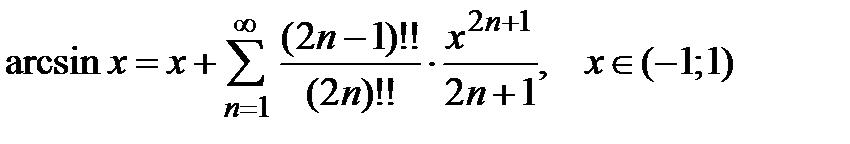(8)

Вывод. Из разложения (5) биномиального ряда при 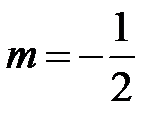и при замене 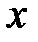на 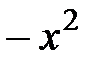получаем разложение в степенной ряд:

.

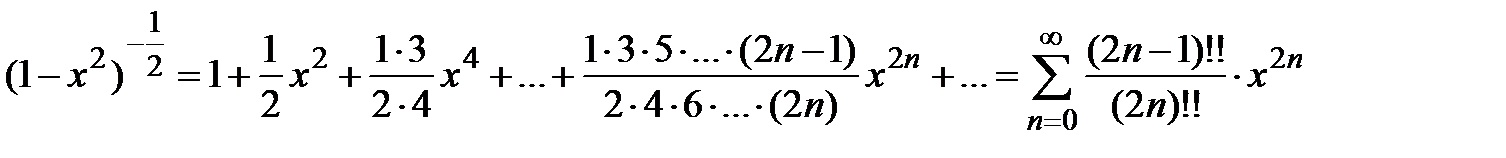Получившийся ряд сходится при 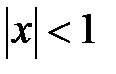. Этот ряд почленно проинтегрируем на отрезке 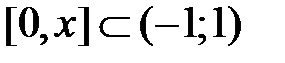, используя свойство 3 (лекция 4, разд. 4.3); при этом интервал сходимости сохранится:

.

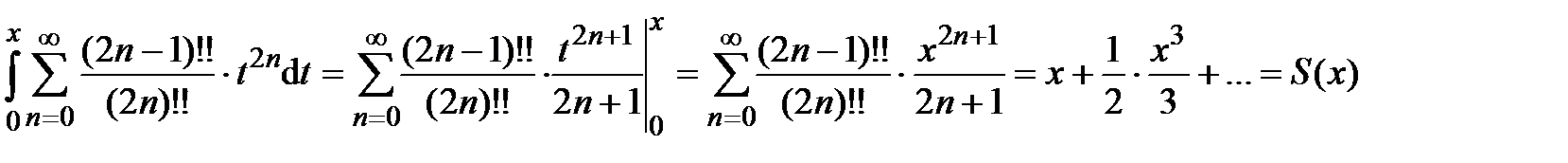Сумма полученного ряда 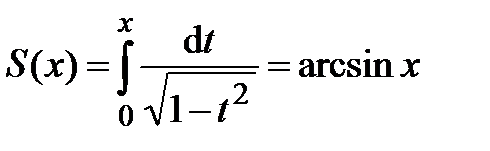. Таким образом,

,

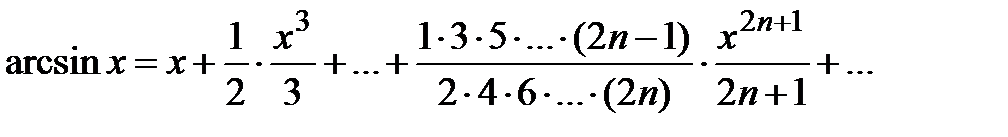т.е. имеет место разложение (8) на интервале сходимости .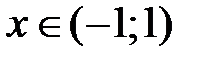

В заключение добавим, что все перечисленные в разделе 5.2 разложения называют основными разложениями элементарных функций в

степенной ряд, которые используются как эталонные для разложения

других функций.