Знакочередующиеся ряды. Признак Лейбница

Определение 1. Числовой ряд ,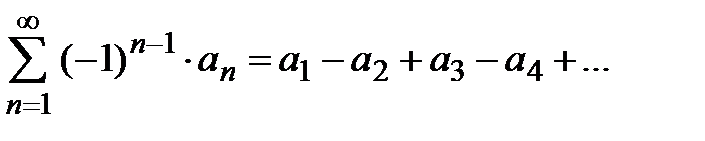
где 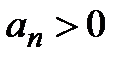, называется знакочередующимся рядом.

Для установления сходимости таких рядов существует достаточный

признак сходимости, называемый признаком Лейбница.

Теорема 1 (признак Лейбница). Пусть числовой ряд 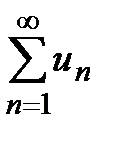удовлетворяет условиям:
1) 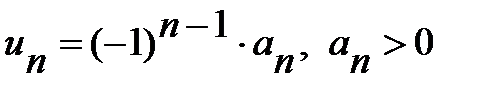, т.е. этот ряд знакочередующийся;
2) члены этого ряда монотонно убывают по абсолютной величине: 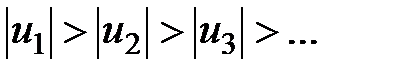т.е. ;
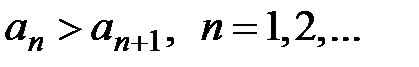3) общий член ряда 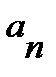стремится к 0, т.е. .
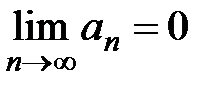Тогда ряд 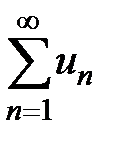сходится и его сумма .

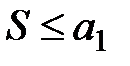Доказательство. 1) Сначала рассмотрим частичную сумму чётного порядка 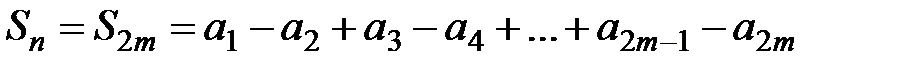и запишем её в виде: 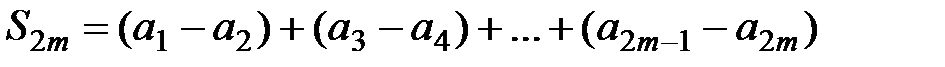. В силу условия 2) теоремы 1 все выражения в скобках положительны, тогда сумма 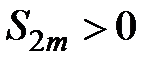и последовательность 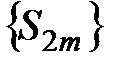монотонно возрастает: .

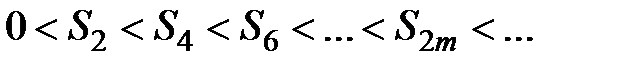Теперь запишем эту сумму иначе: .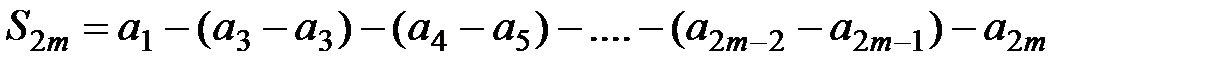
В последнем выражении каждое из выражений в скобках положительно, поэтому 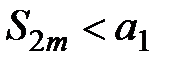, из чего следует, что последовательность 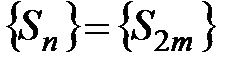является ограниченной, и так как она монотонно возрастает, то она сходится. Другими словами существует 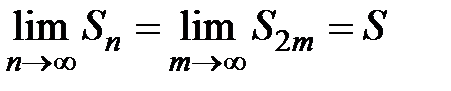, причём .

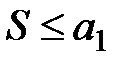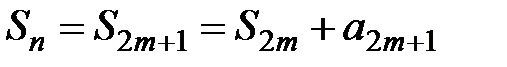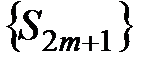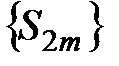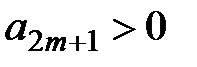2) Рассмотрим частичную сумму нечётного порядка , которая положительна. Можно показать, что последовательность монотонно возрастает, так как монотонно возрастает последовательность и . Запишем выражение для 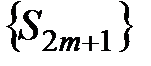в виде: 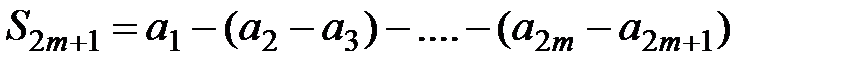, так как все выражения в скобках положительны, то 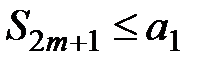. По условию 3) теоремы 1 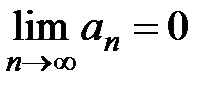, тогда 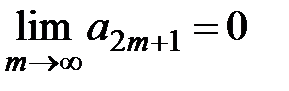, откуда .

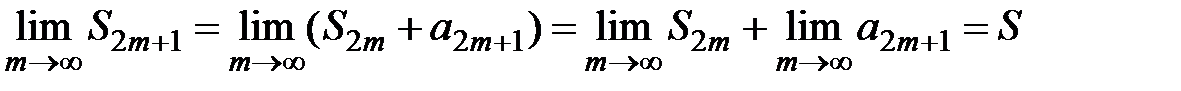Итак, при всех n (чётных или нечётных), 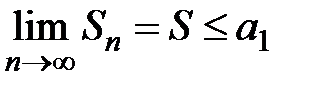, следовательно, исходный ряд сходится. Теорема доказана.

Замечание 1. Признак Лейбница можно также применять к рядам, для которых условия теоремы выполняются с некоторого номера 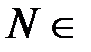N.
Замечание 2. Условие 2) теоремы 1 (признак Лейбница) о монотонности членов ряда существенно.

Пример 1. Исследовать на сходимость ряд .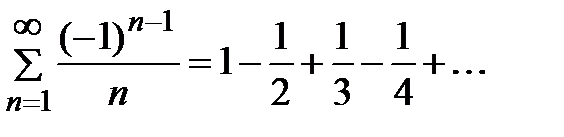

Решение. Обозначим 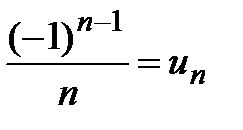. К данному ряду применим признак Лейбница. Проверим выполнение условий теоремы 1: условие 1) ряд знакочередующийся 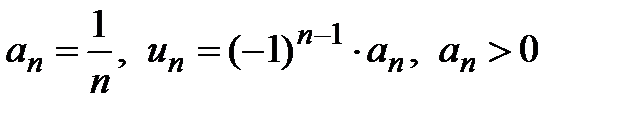; условие 2) выполнено: 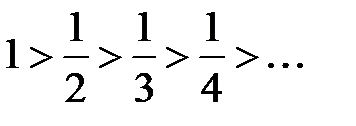; условие 3) также выполнено: 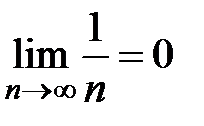. Следовательно, по признаку Лейбница данный ряд сходится, причем его сумма .

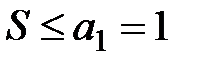Ответ: ряд 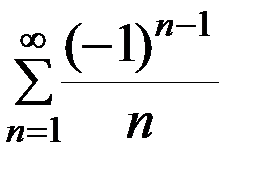сходится.

3.2. Знакопеременные ряды. Абсолютная и условная сходимость.
Достаточный признак сходимости знакопеременных рядов

Числовой ряд 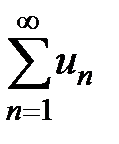, члены которого имеют произвольные знаки (+), (−), называется знакопеременным рядом. Рассмотренные выше знакочередующиеся ряды являются частным случаем знакопеременного ряда; понятно, что не всякий знакопеременный ряд является знакочередующимся. Например, ряд 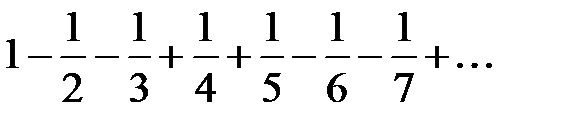− знакопеременный, но не являющийся знакочередующимся рядом.

Отметим, что в знакопеременном ряде членов как со знаком (+), так и со знаком (−) бесконечно много. Если это не выполняется, например, ряд содержит конечное число отрицательных членов, то их можно отбросить и рассматривать ряд, составленный только из положительных членов, и наоборот.

Определение 1. Если числовой ряд 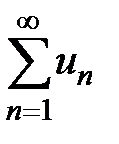сходится и его сумма равна S,
а частичная сумма равна S_n , то 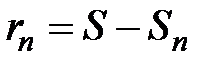называется остатком ряда, причём 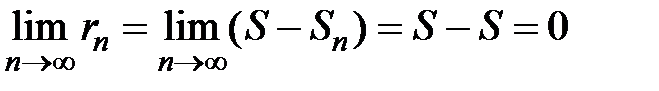, т.е. остаток сходящегося ряда стремится к 0.

Рассмотрим сходящийся знакочередующийся ряд как частный случай знакопеременного ряда

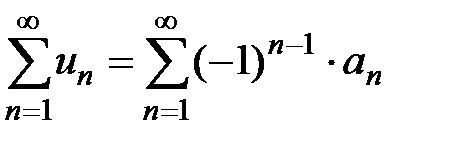, где 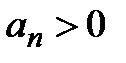. Запишем его в виде 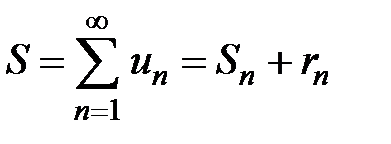, тогда по признаку Лейбница 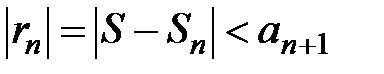; так как 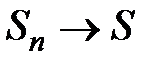, то 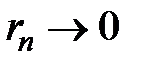, т.е. остаток сходящегося ряда стремится к 0.

Для знакопеременных рядов вводятся понятия абсолютной и условной

сходимости.

Определение 2. Ряд 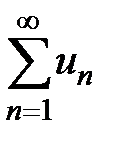называется сходящимся абсолютно, если сходится ряд, составленный из абсолютных величин его членов .

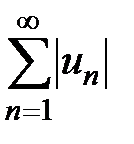Определение 3. Если числовой ряд 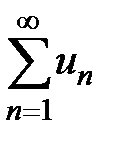сходится, а ряд 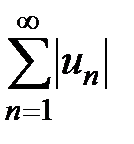, составленный из абсолютных величин его членов, расходится, то исходный ряд называется условно (неабсолютно) сходящимся.

Теорема 2 (достаточный признак сходимости знакопеременных рядов). Знакопеременный ряд 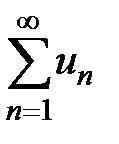сходится, причём абсолютно, если сходится ряд, составленный из абсолютных величин его членов .

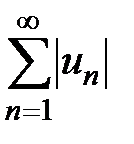Доказательство. Обозначим через 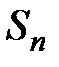частичную сумму ряда 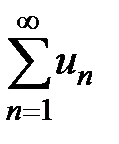: 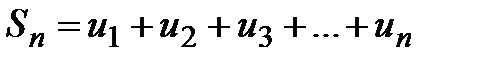, а через 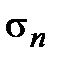− частичную сумму ряда 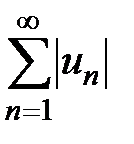: 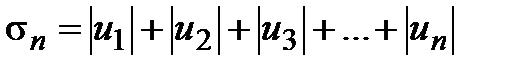. Обозначим через 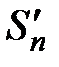сумму всех положительных членов, а через 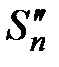сумму абсолютных величин всех отрицательных членов, входящих в 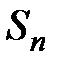. Очевидно, что .

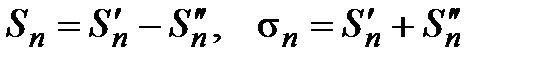По условию теоремы ряд 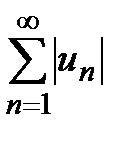сходится, тогда существует 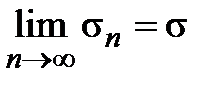, и так как последовательность 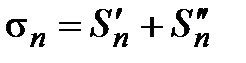− монотонно возрастающая и неотрицательная, то 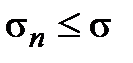. Очевидно, что 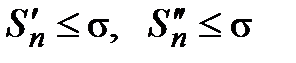, тогда последовательност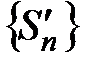и и 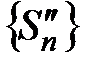являются монотонно возрастающими и ограниченными, причем их пределы равны 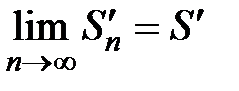и 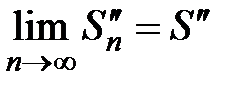. Тогда 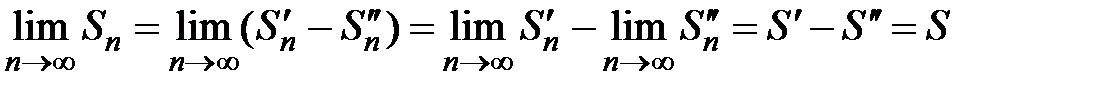. Значит, исходный знакопеременный ряд 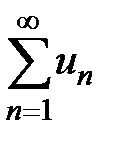сходится и сходится абсолютно. Теорема доказана.

Замечание. Теорема 2 даёт только достаточное условие сходимости знакопеременных рядов. Обратная теорема неверна, т.е. если знакопеременный ряд 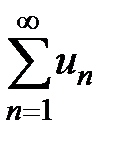сходится, то не обязательно, что сходится ряд, составленный из модулей 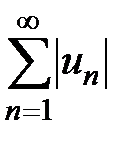(он может быть как сходящимся, так и расходящимся). Например, ряд 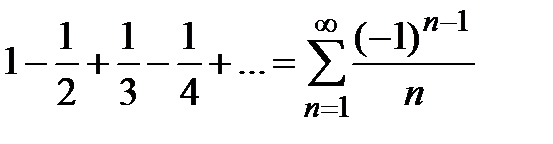сходится по признаку Лейбница (см. пример 1 данной лекции), а ряд, составленный из абсолютных величин его членов, 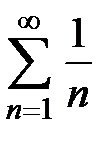(гармонический ряд) расходится.

Пример 2. Исследовать на условную и абсолютную сходимость ряд .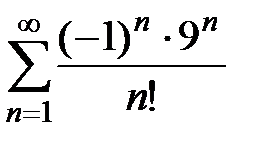

Решение. Данный ряд является знакопеременным, общий член которого обозначим: 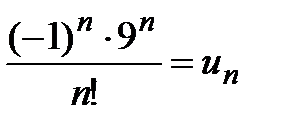. Составим ряд из абсолютных величин 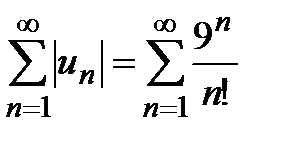и применим к нему признак Даламбера. Составим предел 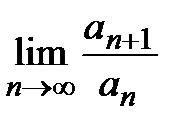, где 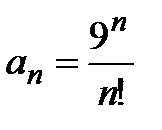, 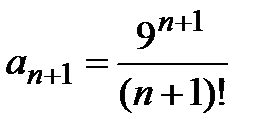. Проведя преобразования, получаем 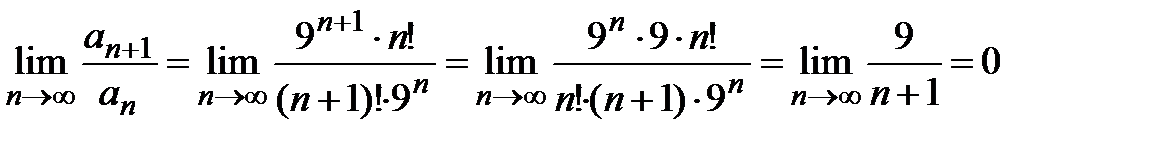. Таким образом, ряд 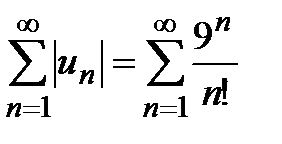сходится, а значит, исходный знакопеременный ряд сходится абсолютно.
Ответ: ряд 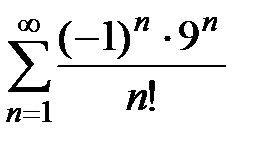абсолютно сходится.

Пример 3. Исследовать на абсолютную и условную сходимость ряд .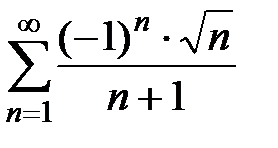

Решение. А) Исследуем ряд на абсолютную сходимость. Обозначим 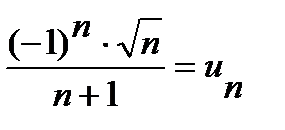и составим ряд из абсолютных величин 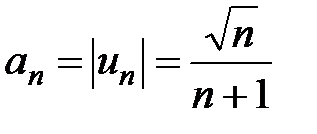. Получаем ряд 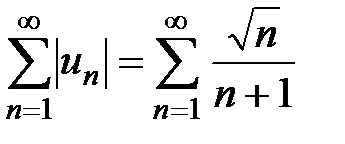с положительными членами, к которому применяем предельный признак сравнения рядов (теорема 2, лекция 2, разд. 2.2). Для сравнения с рядом 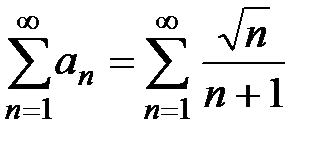рассмотрим ряд, который имеет вид 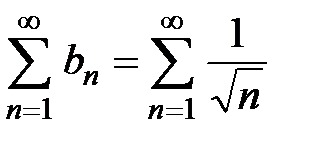. Этот ряд является рядом Дирихле с показателем 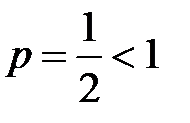, т.е. он расходится. Составим и вычислим следующий предел 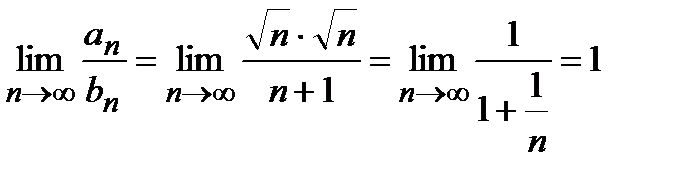. Так как предел существует, не равен 0 и не равен ∞, то оба ряда 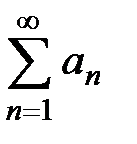и 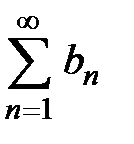ведут себя одинаково. Таким образом, ряд 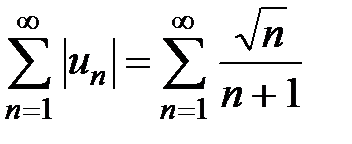расходится, а значит, исходный ряд не является абсолютно сходящимся.

Б) Далее исследуем исходный ряд 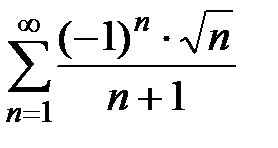на условную сходимость. Для этого проверим выполнение условий признака Лейбница (теорема 1, разд. 3.1). Условие 1): 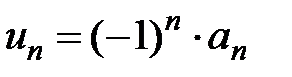, где 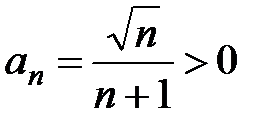, т.е. этот ряд знакочередующийся. Для проверки условия 2) о монотонном убывании членов ряда используем следующий метод. Рассмотрим вспомогательную функцию 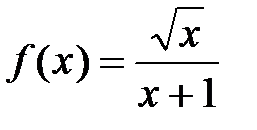, определенную при 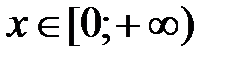(функция такова, что при 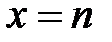имеем 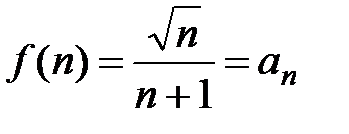). Для исследования этой функции на монотонность найдём её производную: 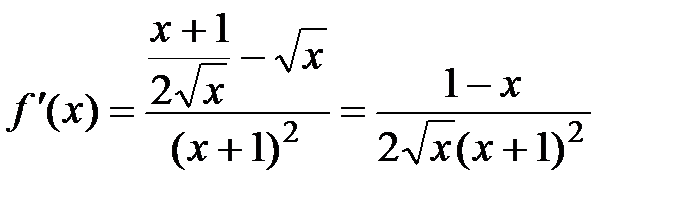. Эта производная 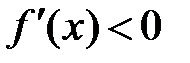при 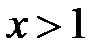. Следовательно, функция 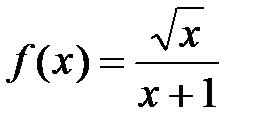монотонно убывает при указанных значениях х. Полагая 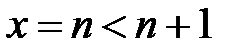, получаем 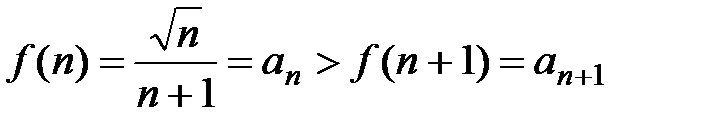, где 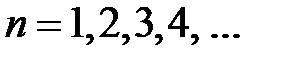. Это означает, чтоусловие 2) выполнено. Для проверки условия 3) находим предел общего члена 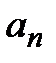: 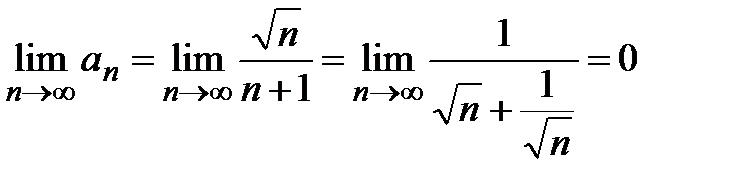, т.е. третье условие выполняется. Таким образом, для исходного ряда выполнены все условия признака Лейбница, т.е. он сходится.

Ответ: ряд 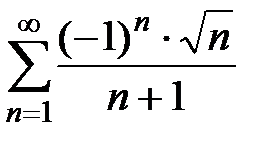условно сходится.