Зависимость и независимость двух случайных величин
Пусть две случайные величины
x = {x1,x2,¼,xn}; h = {у1, у2,¼,уm} (9.6.1)
определены на одном и том же пространстве элементарных исходов. Если Аi (i = 1,2,¼,n) – событие, объединяющее все исходы, приводящие к значению хi случайной величины x, а Вj (j = 1,2,¼,m) – событие, объединяющее все исходы, приводящие к значению уi случайной величины h, то можно определить случайную величину z = x + h, которая принимает все возможные значения 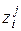 = xi + yj. Каждому такому значению
= xi + yj. Каждому такому значению 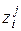 случайной величины z ставится в соответствие вероятность
случайной величины z ставится в соответствие вероятность 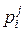 , равная вероятности пересечения событий Аi и Вj:
, равная вероятности пересечения событий Аi и Вj:
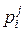 = P(Ai∩Bj).
= P(Ai∩Bj).
Таким образом определяется закон распределения суммы двух случайных величин. Также можно определить законы распределения разности x – h, произведения xh и частного 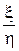 случайных величин (последний – лишь в случае, если h не принимает нулевого значения).
случайных величин (последний – лишь в случае, если h не принимает нулевого значения).
Две случайные величины
x = {x1,x2,¼,xn}; h = {у1, у2,¼,уm},
определённые на одном и том же пространстве элементарных исходов, имеющие законы распределения
| x | х1 | ¼ | xi | ¼ | h | y1 | ¼ | yj | ¼ | |
| Р | 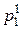 | ¼ | 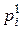 | ¼ | Р | 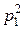 | ¼ | 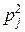 | ¼ |
называются независимыми, если при любых i и j выполняется равенство
Р((x = хi) ∩ (h = yj)) = 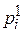
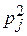
Если это равенство не выполняется хотя бы для одной пары хi, yj, то случайные величины x и h называются зависимыми.
Пример1. Брошены две игральных кости. Число очков, выпавшее на первой кости, – случайная величина x. Число очков, выпавшее на второй кости – случайная величина h. Считаем, что все исходы ((x = i)∩(h = j)) (i = 1,2,¼,6; j = 1,2, ¼,6) равновероятны, всего их 36, поэтому
P((x = i)∩(h = j)) = 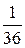
Так как P(x = i) = 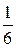 и P(h = j)) =
и P(h = j)) = 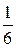 , очевидно, что по определению x и h – независимые случайные величины.
, очевидно, что по определению x и h – независимые случайные величины.
Пример 2. Даны две независимые случайные величины x и h с заданными законами распределения
| x | h | |||||
| Р | 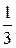 | 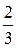 | Р | 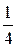 | 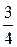 |
Определим случайные величины a и b следующим образом: a = x + h, b = xh. Выясним, являются ли независимыми случайные величины a и b.
Составим закон распределения a. Наименьшее значение a равняется 1. Вероятность события a = 1 равна вероятности события (x = 0)∩(h = 1), которая в силу независимости x и h равна 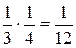 . Событие a = 2 совпадает с событием ((x = 0)∩(h = 2))
. Событие a = 2 совпадает с событием ((x = 0)∩(h = 2))  ((x = 1)∩(h = 1)). Его вероятность равна
((x = 1)∩(h = 1)). Его вероятность равна
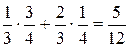 .
.
Максимальное значение a, равное 3, имеет вероятность 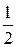 . Таким образом, закон распределения случайной величины a можно представить таблицей
. Таким образом, закон распределения случайной величины a можно представить таблицей
| a | |||
| Р | 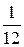 | 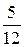 | 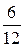 |
Закон распределения b представляется таблицей
| b | |||
| Р | 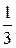 | 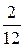 | 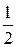 |
Рассмотрим события a = 3 и b = 0. Очевидно, что
Р(a = 3) Р(b = 0) = 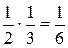
С другой стороны, событие (a = 3)∩(b = 0) – невозможное, так как a = 3 только при x = 1, а b = 0 лишь при x = 0. Отсюда следует, что
Р((a = 3)∩(b = 0)) = 0,
и теперь ясно, что, по крайней мере, в одном случае условие определения независимости для случайных величин a и b не выполняется. Отсюда следует, что эти случайные величины зависимы.
