Корреляционная зависимость случайных величин

Корреляционной называют зависимость, которая проявляется в том, что изменение одной из случайных величин влечёт изменение среднего значения другой случайной величины. Как измерить степень зависимости случайных величин? Когда на лекциях студенты изучают формулу дисперсии суммы двух зависимых случайных величин (которая не равна сумме дисперсии), то исследует математическое ожидание.

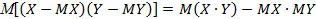
Назовём эту величину корреляционным моментом (или коэффициентом ковариации 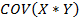от английского слова covariance). Очевидно, что 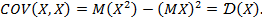Этот коэффициент является измерителем связи случайных величин, так как для независимых случайных величин он равен нулю, для случайных величин, имеющих тенденцию колебаться в одну сторону положителен, а для случайных величин, обладающих закономерностью колебаться в противоположные стороны, отрицателен.

Корреляционный момент имеет размерность, равную произведению размерностей случайных величин, что неудобно: сравнение корреляционных моментов различных систем случайных величин затруднительно. Этот недостаток устраняется введением коэффициента корреляции:

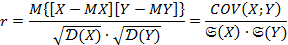
Величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин (в отличие от ковариации), а для независимых случайных величин коэффициент корреляции, как и ковариации, равен нулю.

Абсолютная величина коэффициента корреляции не превышает единицы, поскольку абсолютная величина корреляционного момента не превышает среднего геометрического дисперсии двух случайных величин.

Случайную функцию g 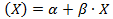называют наилучшим приближенным к случайной величине Y (в смысле среднего квадратического отклонения), если математическое ожидание 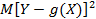принимает наименьшее возможное значение, а функцию 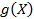, которая доставляет искомый минимум, называют среднеквадратической регрессией Y на X.

С помощью необходимого и достаточного условия экстремума (в многомерном случае, - критерия Сильвестра) выводится уравнение линейной квадратической регрессии Y на X:

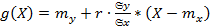где

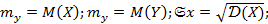
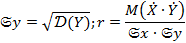
r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1440" w:right="1440" w:bottom="1440" w:left="1440" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 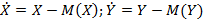. – центрированные случайные величины, математическое ожидание которых равно нулю.

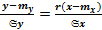Коэффициент 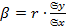называют коэффициентом регрессии Y на X, а прямую 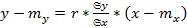– прямой среднеквадратической регрессии Y на X:

Находим, что 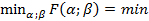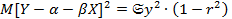и достигается этот min при 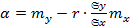; β=r .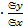

Величину 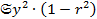называют остаточной дисперсией: она характеризует величину ошибки, которую допускают при замене нелинейной функции Y(X) на линейную .

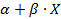При “крайних” значениях коэффициента корреляции r= 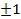остаточная дисперсия 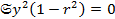, следовательно, не возникает ошибки при представлении Y в виде линейной функции от X, а величины Y и X связаны линейной функциональной зависимостью.

Аналогичен вид линейной среднеквадратической регрессии X на Y:

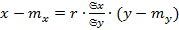, где 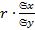– коэффициент регрессии X на Y.

Обе прямые регрессии проходят через точку 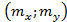– центр совместного распределения X, Y и при 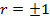совпадают.

Таким образом, для набора значений двух переменных 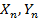, которые изображаются точками на декартовой плоскости, задача “подгонки” функции 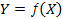под линейную зависимость задаются формулой:

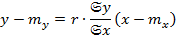
Если данные корреляционной таблицы, при значительном числе наблюдений, среди которых могут быть повторяющиеся, свидетельствуют о криволинейной корреляции, то функции регрессии Y на X могут иметь вид:

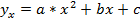(параболическая корреляция)

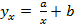(гиперболическая корреляция)

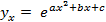(экспоненциальная корреляция)

Для определения такого вида функции строят точки 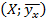и по их расположению делают заключение о примерном виде функции регрессии. При окончательном выборе зависимости принимают во внимание, как экономические соображения неформального характера, так и критерии минимизации остаточной дисперсии для решаемой задачи.

Теория криволинейной корреляции решает ту же задачу, что и теория линейной корреляции: установление формы и тесноты корреляционной связи. Неизвестные параметры уравнения регрессии ищут по МНК, а тесноту связи определяют по отношению межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению признака.

Например, в случае параболической корреляции неизвестные параметры a; b; c находятся из системы линейных алгебраических уравнений с положительным детерминантом (по правилу Крамера):

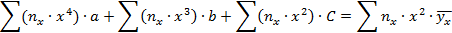
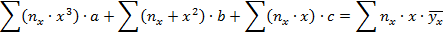
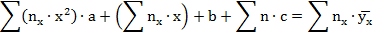
где 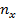- кратность появления значения x, то есть пары чисел 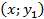; 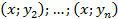реально наблюдаются > 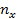раз.

Пример. Найти выборочное уравнение регрессии Y на X в случае параболической корреляции и решить его по данным корреляционной таблицы 2.

Здесь X – вводы основных производственных фондов (ОППФ, в млн. руб.);

Y – капитальные вложения в ОППФ из трёх различных источников финансирования.

Таблица 2

Корреляционная зависимость случайных величин

Y	X
	1,1	1,2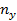
7,5
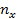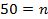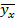		6,73	7,5

Составляем расчетную таблицу.

Таблица 3

Расчетная таблица для определения оценок коэффициентов корреляционной зависимости

x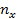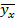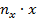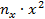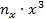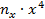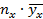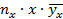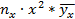
1,1		6,73	36,3	39,93	43,93	48,32	222,1	244,3	268,73
1,2		7,5	10,8	12,96	15,55	18,66	67,5		97,2
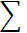		-	55,1	60,89	67,48	74,98	337,59	373,3	413,93

Подставляя в нормальную систему МНК суммы нижней строки таблицы, получим систему линейных уравнений:

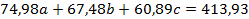
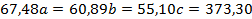
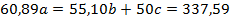
Решая систему методом Крамера или методом Жордана – Гаусса, определяем оценки неизвестных параметров: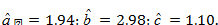

Параболическая регрессия Y на X имеет вид: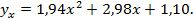

Приложение 3