Понятие дифференциального уравнения первого порядка. Решение ДУ, интегральная кривая, частное решение, начальные условия, задача Коши

Опр:дифференциальным уравнением называется уравнение, в котором неизвестная функция входит под знаком производной или дифференциала.

- если неизвестная функция зависит от одной переменной, то дифференцируемое уравнение [ДУ] называется обыкновенным

- если дифференцируемая функция зависит от двух или нескольких переменных то ДУ называется уравнением в частных производных

Запишем общий вид обыкновенного ДУ

F(x,y,y’,y”,…,y⁽ⁿ⁾)=0 n-го порядка

F – заданная функция связывающая независимую переменную Х, неизвестную функцию y=y(x) и ее производные y,y’,y”,…,y⁽ⁿ⁾

Порядок старшей производной, входящей в дифференцируемое уравнение называется порядком этого дифференцируемого уравнения

Решением ДУ называется дифференцируемая функция которая при подстановке в дифференцируемое уравнение обращает его в тождество.

Одной из основных задач: нахождение решений ДУ в простейших случаях сводится к нахождению интеграла => процесс нахождения решения ДУ – интегрирование ДУ

А график решения – интегральной кривой

ОДУ первого порядка. Общий вид.

F(x,y,y’)=0 (1)

х,у – могут отсутствовать х – независмая переменная у – ф-ция неизвестная у=у(х)

y’ – должен быть обязательно

F – заданная функция 3-х переменных

Опр: y’=f(x) (**) если его (1) можно разрешить относительно старшей произ-ой y’=f(x,y), то оно называется разрешенным относительно произ-ой

y’=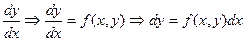

p(x,y)dx + q(x,y)dy = 0

43. Теорема о существовании и единственности решения задачи Коши (без док). Определение общего решения ДУ.(**)

Пусть задана ДУ y^|=f(x,y). Пусть f(x,y) и f^|_y – являются непрерывными функциями в некоторой области D.

Тогда для любых точки А₀(х₀, у₀) принадлежащей D существует единственное решение у=у(х) уравнения y’=f(x) и это решения удовлетворяет условию у₀=φ(х₀)(***)

Числа х₀, у₀ – начальные значения для решения у=у(х), а соотношение (***) над начальными условиями этого решения

геометрических смысл теорем. ч/з каждую (.)-у (х₀, у₀) принадлеж-ую D, проходит одна и только одна интегральная кривая, поэтому вся область D, где f(x, y), f^|_y – непрерывные, покрытые интегральными кривыми, каждые нигде не пересекаются.

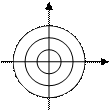х²+у²=С², меняя С мы получаем множество решений

интегральные кривые (решения ДУ)

Задача Коши.

Задача нахождения интегральной кривой, проходящей через точкуА₀ (х₀, у₀)

Опр. Общем решение ДУ(**) называется функция у= φ(х, с) зависящая от одного произвольного постоянного с, которая удовлетворяет условиям.

1. при любых с фун-ия у= φ(х, с) удовлетворяет д.у. y’=f(x)

2. для любого начального условия у=у(х₀) можно найти единственные с=С₀, такое что у=у(х, С₀) – удовлетворяет данному условию.

44. Понятие особой точки. Виды особых точек.

Определение:

1. точки разрыва функции f(x,y) (при приближении к точке разрыва (x₀,y₀) функция неограниченно возрастает по модулю)

2. 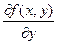разрывная (т.е. )

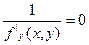такие точки называются особыми.

Опр. Кривая состоящая из особых точек над особой кривой.

Опр. Решение ДУ, для которого график особая кривая над особым решением

Классификация особых точек:

1. точка с координатами (0,0), через которую проходят все интегральные кривые наз. узлом

у

х

2. точка с координатами (0,0) наз. седлом через которую проходит 2-е интегральные или конечное число интегральных кривых

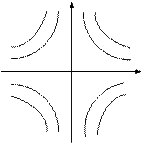
Ось y=0 и x=0-интегральные кривые через точки (0,0)

3. особая точка, (0,0) окрестность которой заполняется семейством замкнутых интегральных кривых наз. центром.

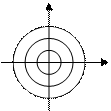
4. особая точка, вокруг которой все интегральные кривые делают бесконечное число оборотов наз. фокусом.

45. Основные виды ДУ: с разделяющимися переменными, однородные, линейные первого порядка, Бернулли, в полных дифференциалах. Уравнения, не разрешенные относительно производной: Клеро, Лагранжа.