Решение задачи Коши для дифференциального уравнения 1-го порядка с фиксированным шагом
В курсовой работе необходимо указанными методами решить задачу Коши для дифференциального уравнения 1 – го порядка на отрезке [ Хо, Хк] с шагом h и начальным условием У(Хо)=Уо.
Ответ должен быть получен в виде таблицы результатов:
| X | Y(1) | Y(2) | Y(T) |
| X0 | Y0(1) | Y0(2) | Y(X0) |
| X1 | Y1(1) | Y1(2) | Y(X1) |
| … | … | … | … |
| Xk | Yk(1) | Yk(2) | Y(Xk) |
где : Y (1), Y (2) - решения, полученные различными численными методами, Y(T) – точное решение дифференциального уравнения.
Возможно представление результатов решения не в виде таблицы, а в виде списков.
Данные таблицы визуализировать на форме в виде графиков.
Исходные данные для различных вариантов представлены в таблице.
Перед вычислением последнего столбца таблицы результатов необходимо из начальных условий вычислить значение коэффициента с, используемое в общем решении.
Таблица 1 - Задания для курсовых работ
| № варианта | Дифференциальные уравнения | X0 | Xk | h | Y0 | Общее решение | Методы решения |
| x×y×dx+(x+1) ×dy=0 | 1.2 | 0.1 | y=c×(x+1) ×exp(-x) | Эйлер, Рунге-Кутт | |||
| y¢=x×y 2+2×x×y | 0.2 | -1.8 | y=-2/(1+c×exp(-x2)) | Эйлер, Эйлер модифицированный | |||
y¢=2× 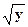 ×ln(x) ×ln(x) | 0.1 | y=(x×ln(x)-x+c) 2 | Рунге-Кутт, Эйлер модифицированный | ||||
| y¢×ctg(x)=2-y | 0.1 | y=2-cos(x) | Эйлер, Рунге-Кутт | ||||
| y¢×x=3×y | 1.4 | 0.05 | y=c×x 3 | Эйлер, Эйлер модифицированный | |||
| yy¢+x=1 | 0.1 | y= 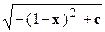 | Рунге-Кутт, Эйлер модифицированный | ||||
| y¢=-0.05×y | 0.1 | y=c×exp(-0.05•x) | Эйлер, Рунге-Кутт | ||||
| y¢=4×x-2×y | 1.2 | 0.1 | 2.4 | y=c×exp(-2×x)+2×x-1 | Эйлер, Эйлер модифицированный | ||
| (y2-2x×y)dx+x2dy =0 | 0.1 | 0.2 | y=x2/(c+x) | Рунге-Кутт, Эйлер модифицированный | |||
| (y¢-y) ×x=e x | 0.1 | y=exp(x)(ln|x|+c) | Эйлер, Рунге-Кутт | ||||
| y¢×x=exp(x)-y | 1.0 | 0.1 | y=[exp(x)+1-e]/x | Эйлер, Эйлер модифицированный | |||
| y¢×x=4y | 1.4 | 0.05 | y=x4×c | Рунге-Кутт, Эйлер модифицированный | |||
| y¢×(x+1)=y + 2 | 0.8 | 0.1 | y=(x+1) ×c-2 | Эйлер, Рунге-Кутт | |||
| 2×x×y×dx-(x+1)×dy=0 | 0.8 | 0.05 | y=e2x× c/(x+1)2 | Эйлер, Эйлер модифицированный | |||
| y¢+2×x×y=x×exp(-x 2) | 0.1 | y=exp(-x 2)(c+x 2/2) | Рунге-Кутт, Эйлер модифицированный | ||||
| y¢+y=cos(x) | p/2 | p/10 | y=c×exp(-x)+[cos (x)+ +sin (x)] /2 | Эйлер, Рунге-Кутт | |||
| y¢×x=y+1 | 0.5 | -0.9 | y=c×x-1 | Эйлер, Эйлер модифицированный | |||
| 3x2 – y¢=0 | 1.8 | 0.1 | y=x3-c | Рунге-Кутт, Эйлер модифицированный | |||
| x×y¢+y=y 2×ln(x) | 1.6 | 0.1 | y=[1+ln (x)+c×x]-1 | Эйлер, Рунге-Кутт | |||
| (1+x 2)×dy+y×dx=0 | 1.8 | 0.1 | ln|y|=-arctg(x)+c | Эйлер, Эйлер модифицированный | |||
| y¢=y/x+sin(y/x) | 1.5 | 0.05 | p/2 | y=2×x×arctg(c×x) | Рунге-Кутт, Эйлер модифицированный | ||
| x×y¢-y=x 2×cos(x) | 1.8 | 2.4 | 0.1 | 0.5 | y=x×[sin(x)+c] | Эйлер, Рунге-Кутт | |
| y¢+y/x=3/x | 1.8 | 0.1 | y=3(x-1)/x | Эйлер, Эйлер модифицированный | |||
| y¢=2×x2+2×y | 0.1 | y=1.5×exp(2×x)-x2-x-c | Рунге-Кутт, Эйлер модифицированный | ||||
| y¢×sin(x)-y×cos (x)=0 | p/2 | 3p/4 | p/20 | y=sin (x) | Эйлер, Рунге-Кутт | ||
| (1+y 2) ×dx=x×dy | 1.5 | 0.05 | y=tg( ln (c×x) ) | Эйлер, Эйлер модифицированный | |||
| (x-y) ×dx+x×dy=0 | 1.2 | 0.1 | y=x×(c-ln (x)) | Рунге-Кутт, Эйлер модифицированный | |||
| x×y¢=y× [ln (y)-ln (x)] | 0.1 | y=x×exp(1+c×x) | Эйлер, Рунге-Кутт | ||||
| x 2+x×y¢=y | 1.4 | 0.05 | y=x-x 2 | Эйлер, Эйлер модифицированный | |||
| y¢+2×x×y=2×x×y 2 | 1.2 | 0.02 | y=[(1+c×exp(x 2)]-1 | Рунге-Кутт, Эйлер модифицированный |
Литература
1. Демидович Б.П., Марон И.А., Шувалова Э.З., Численные методы анализа. - М.: Физматгиз, 1963.-400 с.
2. Иванова Т.П., Пухова Г.В. Вычислительная математика и программирование. М.: Просвещение, 1978. – 320 с.
3. Плис А.И., Сливина Н.А. Лабораторный практикум по высшей математике: Учеб. пособие для втузов. - М.: Высшая школа, 1983. - 208 с.
4. Браун С. Visual Basic 6. Учеб. курс. – СПб.: Питер, 2006. – 574 с.
