Условия коллинеарности векторов

Два вектора коллинеарные, если отношения их координат равны.

Два вектора коллинеарные, если их векторное произведение равно нулю.

Вычисление координат некоторой точки С, которая делит заданный отрезок АВ в определенном отношении, может быть выполнено по формулам:

хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ),

где (хА; уА) и (хВ; уВ) – координаты концов заданного отрезка АВ; число λ = АС/СВ – отношение, в котором отрезок АВ делится точкой С, имеющей координаты (хС; уС).

Если отрезок АВ делится точкой С пополам, то число λ = 1 и формулы для хС и уС примут вид:

хС = (хА + хВ)/2, уС = (уА + уВ)/2.

6) Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла междуними.

1. Скалярное произведение обладает переместительным свойством: ab=ba

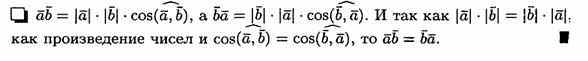
скалярное произведение векторов равно сумме произведений их одноименных координат.

7) Векторным произведением вектора 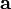на вектор 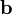в пространстве 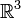называется вектор 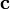, удовлетворяющий следующим требованиям:

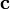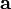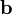длина вектора равна произведению длин векторов и на синус угла 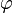между ними: ;

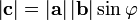вектор 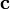ортогонален каждому из векторов 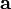и ;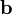

вектор 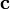направлен так, что тройка векторов 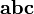является правой;

в случае пространства 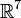требуется ассоциативность тройки векторов .

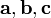Геометрический смысл векторного произведения: модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах как на сторонах.

Если два вектора 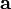и 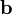определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе

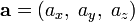
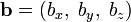
а система координат правая, то их векторное произведение имеет вид

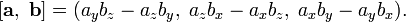
8) Сме́шанное произведе́ние 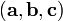векторов 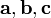— скалярное произведение вектора 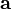на векторное произведение векторов 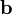и :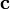

.

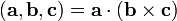Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).

Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами .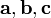

Свойства

Смешанное произведение кососимметрично по отношению ко всем своим аргументам:

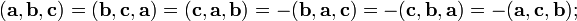
т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что

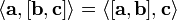
Смешанное произведение 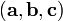в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов 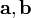и :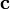

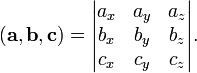
Смешанное произведение 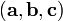в левой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов 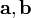и 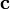, взятому со знаком "минус":

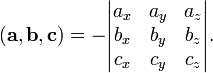
В частности,

Если любые два вектора коллинеарны, то с любым третьим вектором они образуют смешанное произведение равное нулю.

Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.

Геометрический смысл — Смешанное произведение 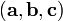по абсолютному значению равно объёму параллелепипеда (см. рисунок), образованного векторам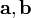и и 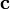; знак зависит от того, является ли эта тройка векторов правой или левой.

Квадрат смешанного произведения векторов равен определителю Грама, определяемому ими

Смешанное произведение удобно записывается с помощью символа (тензора) Леви-Чивита:

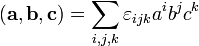
Смешанное произведение в координатах

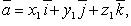
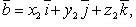
Если 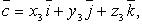то

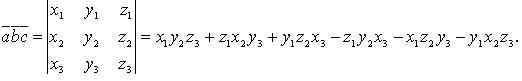
9) Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

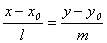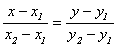, - x = x₀ + lt, y = y₀ + mt - у = kx + b -

1) С = 0 - прямая Ах + Ву = 0 проходит через начало координат.

2) В = 0 - прямая Ах + С = 0 параллельна оси Оу (так как нормаль к прямой {A,0} перпендикулярна оси Оу).

3) А = 0 - прямая Ву + С = 0 параллельна оси Ох.

4) В=С=0 – уравнение Ах = 0 определяет ось Оу.

5) А=С=0 – уравнение Ву = 0 определяет ось Ох.

10) Если две прямые l₁ и l₂ лежат на плоскости, то возможны три различных случая их взаимного расположения: 1)пересекаются (т.е. имеют одну общую точку); 2) параллельны и не совпадают; 3) совпадают.

Выясним, как узнать, какой из этих случаев имеет место, если эти прямые заданы своими уравнениями в общем виде:

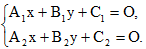(12)

Следовательно, чтобы найти координаты точки пересечения прямых l₁ и l₂, надо решить систему уравнений(12):
1) если система (12) имеет единственное решение, то прямые l₁ и l₂ пересекаются;
2) если система (12) не имеет решения, то прямые l₁ и l₂ параллельны;
3) если система (12) имеет множество решений, то прямые l₁ и l₂ совпадают.

11) Общее уравнение (полное) плоскости

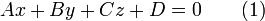
где 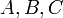и 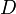— постоянные, причём 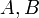и 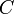одновременно не равны нулю; в векторной форме:

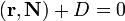
где 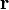— радиус-вектор точки 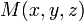, вектор 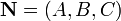перпендикулярен к плоскости (нормальный вектор). Направляющиекосинусы вектора :

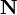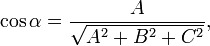
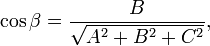
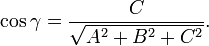
Если один из коэффициентов в уравнении плоскости равен нулю, уравнение называется неполным. При 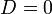плоскость проходит через начало координат, пр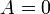и (или 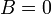, 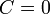) П. параллельна оси 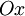(соответственно 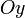или 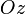). Пр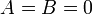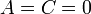и ( , или 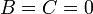) плоскость параллельна плоскости 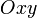(соответственно 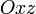или ).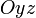

Уравнение плоскости в отрезках:

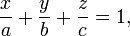
где 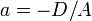, , 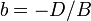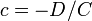— отрезки, отсекаемые плоскостью на осях 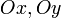и .

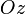Уравнение плоскости, проходящей через точку 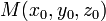перпендикулярно вектору нормали :

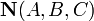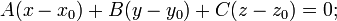
в векторной форме:

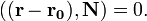
Уравнение плоскости, проходящей через три заданные точки 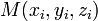, не лежащие на одной прямой:

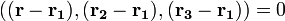
(смешанное произведение векторов), иначе

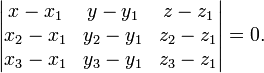
Нормальное (нормированное) уравнение плоскости

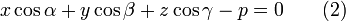
в векторной форме:

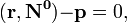
где 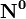- единичный вектор, 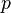— расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель

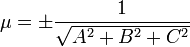
(знак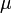и и 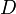противоположны).

12) Теорема. Пусть

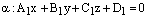и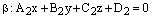

– общие уравнения двух плоскостей. Тогда:

1) если 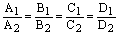, то плоскости совпадают;

2) если 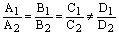, то плоскости параллельны;

3) ес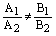ли или 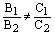, то плоскости пересекаются и система уравнений

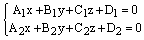(6)

является уравнениями прямой пересечения данных плоскостей.

Теоремы

Если прямая, пересекающая плоскость, перпендикулярна двум прямым, лежащим в этой плоскости и проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.

Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.

13) Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса, есть величина постоянная. В канонической для эллипса системе координат уравнение эллипса имеет вид:

.

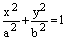14) Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.

Каноническое уравнение: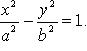

15) Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.

Каноническое уравнение: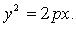

16) Числовая последовательности и ее предел.

Функция f(x) называется функцией целочисленного аргумента, если множество значений x, для которых она определена, является множеством всех натуральных чисел1, 2, 3,… Примером функции целочисленного аргумента может служить сумма n первых чисел натурального ряда. В данном случае

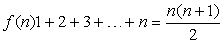
Числовой последовательностью называется бесконечное множество чисел

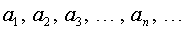(1)

следующих одно за другим в определенном порядке и построенных по определенному закону, с помощью которого 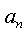задается как функция целочисленного аргумента, 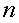т.е. .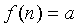

Число А называется пределом последовательности (1), если для любого 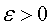существует число 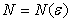, такое, что при 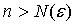выполняется неравенство 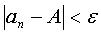. Если число А есть предел последовательности (1), то пишут

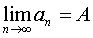
Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся.

Для сходящихся последовательностей имеют место теоремы:

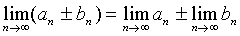
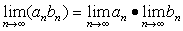
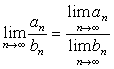
если .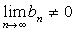

17) Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.

Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности 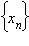такой, что 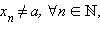сходящейся к числу a, соответствующая последовательность значений функции 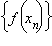сходится к числу A.

Окрестностное определение по Коши

Значение 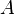называется пределом (предельным значением) функции 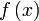в точке 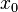, если для любой окрестност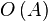и точки 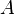существует выколотая окрестность 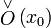точки 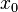такая, что образ этой окрестности 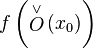лежит в .

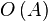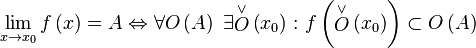
Предел по базе множеств

Наиболее общим определением является определение предела функции по базе (по базису фильтра, по фильтру).

Пусть 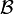— некоторая база подмножеств области определения. Тогда

число 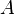называется пределом функции по (при) базе 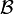, если для всякого 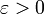найдётся такой элемент 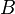базы, что для любого 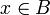выполнено .

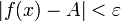Если 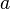— предельная точка множества 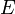, то это означает, что каждая проколотая окрестность точки в множестве 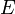не пуста, а, значит, существует база проколотых окрестностей в точке 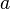. Эта база имеет специальное обозначение « 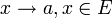» и читается «при 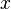, стремящемся к 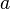по множеству 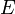». Если область определения функции 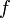совпадает с 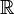, то значок множества опускается, тогда база обозначается совсем просто « 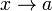» и читается «при 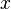, стремящемся к ».

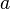18) Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известныхматематических тождеств со взятием предела. Особенно известны:

Первый замечательный предел:

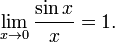
Второй замечательный предел:

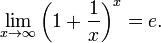
19) Как известно, сумма, разность и произведение двух б.м.ф. есть функция бесконечно малая. Отношение же двух б.м.ф. может вести себя различным образом: быть конечным числом, быть бесконечно большой функцией, бесконечно малой или вообще не стремиться ни к какому пределу.

Сведём теперь полученные формулы в итоговую таблицу. Всюду в ней .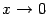

	.
	.
	.
	.
	.
	( ).
	.
	( ).
	.

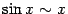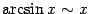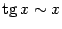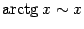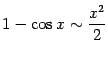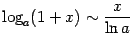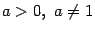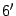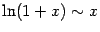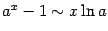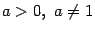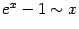20)Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.

Точки разрыва

Если условие, входящее в определение непрерывности функции в некоторой точке, нарушается, то говорят, что рассматриваемая функция терпит в данной точке разрыв. Другими словами, если 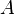— значение функции 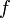в точке 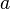, то предел такой функции (если он существует) не совпадает с 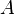. На языке окрестностей условие разрывности функции 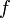в точке 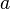получается отрицанием условия непрерывности рассматриваемой функции в данной точке, а именно: существует такая окрестность точки 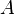области значений функции 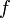, что как бы мы близко не подходили к точке 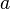области определения функции 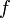, всегда найдутся такие точки, чьи образы будут за пределами окрестности точки .

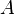Точки разрыва первого и второго рода

если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;

если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.

21) Производной функции 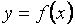называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю