Часть 1. Расчет ПИД-реулятора по заданной LAX и параметрам.

По вопросам к выполнению расчета и тренировки на tr_PID писать сюда: http://vk.com/airnave

График взят из тренажера tr_PID (в конце этого документа есть пояснения для тренировки расчета в tr_PID, для того, чтоб сверить правильность рассчитанных коэффициентов и написанной программы. Т.е для тренировки сначала выполняйте tr_PID, а потом этот расчет)

Ограничение подъема усиления дифференциальной составляющей h = 10

Перерегулирование = 5%

Исходя из заданной величины перерегулирования из таблицы выбираем k_e

Перерег., %
ke	0.35	0.4	0.5	0.6	0.75

k_e = 0.5

Находим общий коэффициент усиления К₀

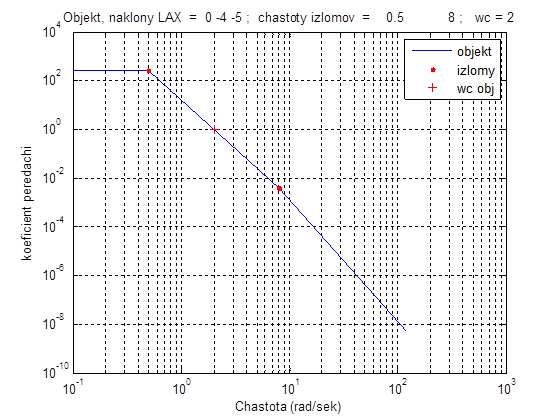
Для этого на графике находим частоту среза wc. В нашем примере wc = 2. Все наклонные, которые расположились ниже wc, в расчетК₀не берем!

К₀ вычисляется как произведение отношений большей частоты к меньшей в степени модуля наклона меду ними (от wc и все, что выше, справа налево)

В нашем примере только одна частота выше wc, значит всего один множитель, значит К₀ будет равно частоты среза и предыдущей частоты: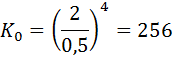

где 2 – это wc, 0.5 – частота первого излома, 4 – это наклон между точками частот излома, между 0.5 и 2. Все остальные наклоны и частоты излома, которые находятся ниже wc = 2 (на графике ниже пунктирной линии уровня 10⁰) откидываем и в расчет не берем.

Если бы wc была больше 8, допустим wc = 9. Выходит, что выше уровня частоты среза (линии 10⁰) лежали бы уже 2 точки излома (0.5 и 8) с теми же наклонами. Значит формула расчета К₀ имела бы вид: 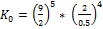Т.е. фактически мы бы двигались от wc и выше (справа налево), каждый раз деля большую частоту на меньшую в степени модуля наклона между ними.

Дальше расставляем частоты w1, w2… wn исходя из заданного графика:

w1, w2… wn расставляются строго по увеличению значения частот. Для данного графика w1=w2=w3=w4=0.5, т.к. обьект изменил свой наклон в частоте излома 0.5 с 0 до -4, т.е. изменение равно 4, значит в этой точке 4 частоты (w1,w2,w3,w4). wc исходя из графика осталась такой же =2. На частоте излома 8 наклон объекта изменился с -4 до -5, т.е. изменение рано 1, значит тут отмечачем одну частоту w5 = 8

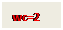
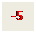
Рассчитываем W(s) по формуле

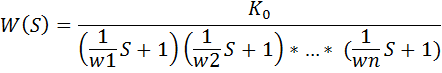
Т.к. на частоте 0.5 наклон изменяется на 4, то w1=w2=w3=w4=0.5. Формула имеет вид:

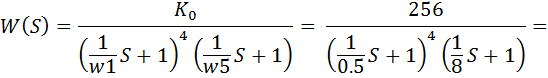
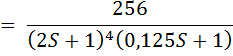
Вычисляем суммарную некомпенсируемую инерционность Tsum:

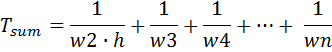
Первая, самая маленькая частота (w1) в расчете Tsum никогда не учитывается!, вторая (w2) умножается на h , остальные (w4, w5 … wn) используются все как есть.

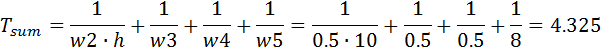
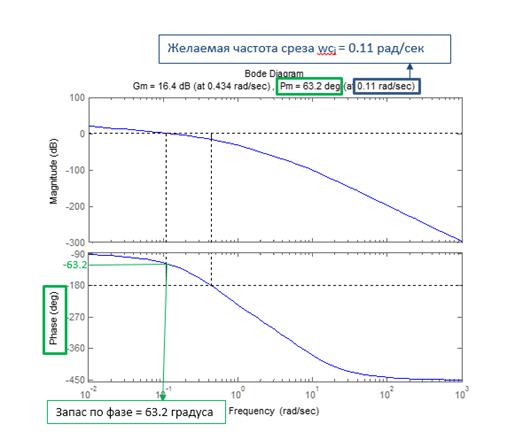
Теперь находим желаемую wc_j частоту среза:

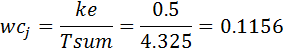
Находим коэффициент интегральный

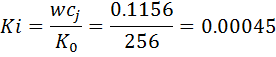
Находим передаточная функция (zpk-форма) ПИД-регулятора. В расчете участвуют только частоты w1 и w2, все остальные(w3,w4…wn)всегда отбрасываются!

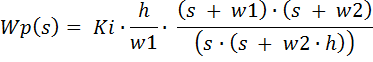
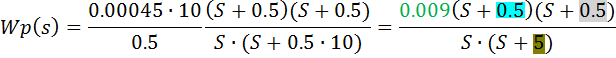
Так же запишем еще раз W(s), рассчитанную выше:

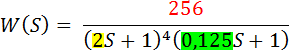
Составление программы:

Цветом обозначены значения, которые мы брали из формул, рассчитанных выше. Очень важно не перепутать большие и малые буквы, следить внимательно за обозначениями и синтаксисом: не путать и не терять точки, запятые, точки с запятыми и пробелы.

Программу лучше написать отдельно в новом документе MS Word или в txt файле, потом скопировать все целиком и ввести в рабочее окно matlab и нажать в конце, если понадобится клавишу Enter или запустить выполнение. Подключать рабочий каталог trenag не обязательно. На разных версиях matlab бывают разные глюки, иногда перед Step(W) нужно еще раз писать figure

В записи W1=tf([1],[2 1]) и в последующих W2 … Wn, так же как и Wp=zpk([-0.5 -0.5],[0 -5],0.009) в квадратных скобках между значениями стоят пробелы.

В записи Wp=zpk([-0.5 -0.5],[0 -5],0.009)коэфф. уже со знаком «-», т.е. всегда отрицательны!

В примере из-за того, что в формуле W(s) в знаменателе первый множитель (2S+1)^4, т.е. в степени 4, так как частоты W1=W2=W3=W4 равны между собой, поэтому в программе, для удобства, они одинаково записаны 4 раза. У вас эти множители могут быть различными и их количество может тоже отличатся.

Программа для нашего примера:

Прописываем путь к папке trenag

addpath c:\trenag

W1=tf([1],[2 1])

W2=tf([1],[2 1])

W3=tf([1],[2 1])

W4=tf([1],[2 1])

W5=tf([1],[0.125 1])

Ws=256*W1*W2*W3*W4*W5

Wp=zpk([-0.5 -0.5],[0 -5],0.009)

W=feedback(Wp*Ws,1)

figure; step(W)

figure; margin(Ws*Wp)

aLAX(Ws)

khar_sysz3(W)[DA1]

После ее выполнения появятся 3 графика[DA2] :

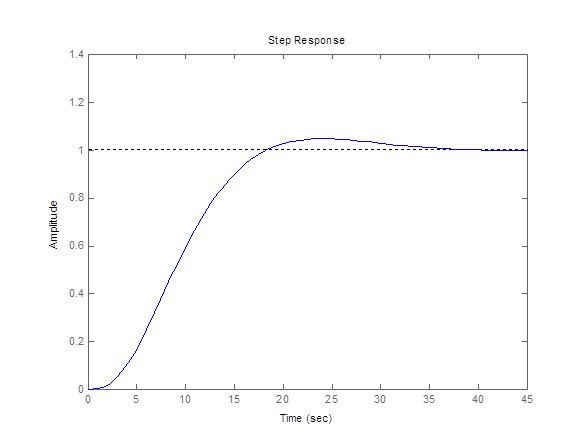
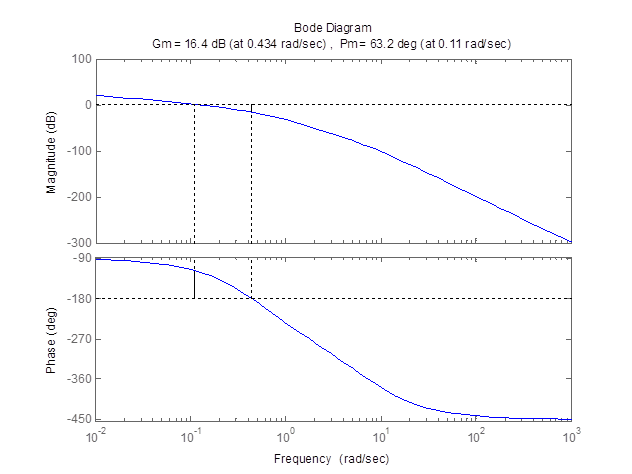
Пояснения к графикам:

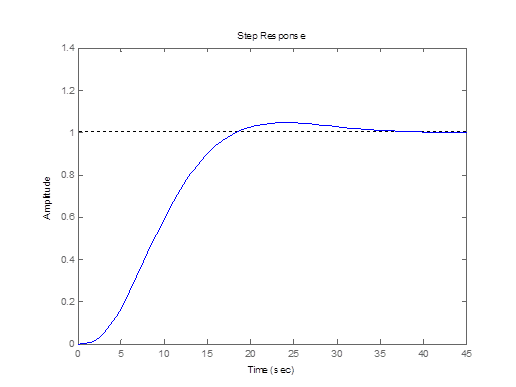Горб над единичной пунктирной линией означает наше перерегулирование в 5% (при k_e=0.5), которое мы задавали в исходных данных. При перерегулирование в 0% (k_e=0.35) график плавно стремиться к единичному уровню (пунктирная линия). Чем выше перерегулирование, тем выше k_e и выше горб. Снизу в Time(sec) указана длительность процесса. Вхождение – время до первого пересечения с единичным уровнем.

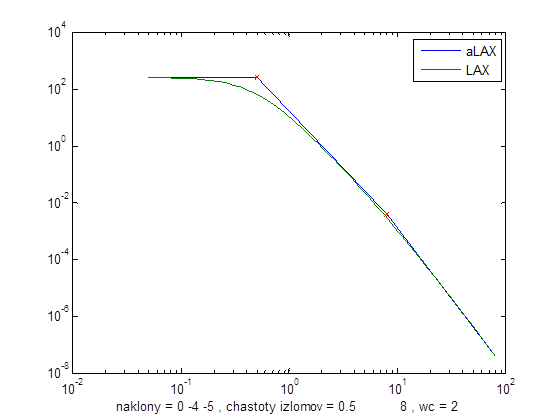
Восстановленная ЛАХ объекта из исходных данных[DA3]

Команда aLAX(Ws)

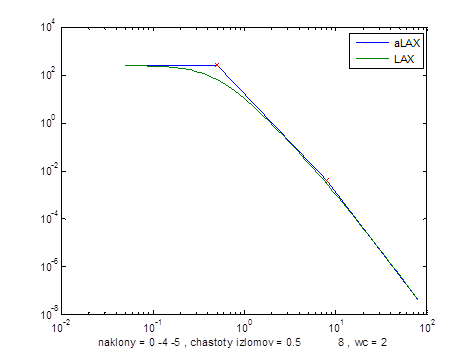
Наклоны 0 -4 -5, частоты изломов 0.5 , 8, частота среза 2 равны исходным данным.

Часть 2. tr_PID