Методом крутильных колебаний
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФГБОУ ВПО РЫБИНСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ П.А. СОЛОВЬЕВА
КАФЕДРА ОБЩЕЙ И ТЕХНИЧЕСКОЙ ФИЗИКИ
| УТВЕРЖДЕНО на заседании методического семинара кафедры ОиТФ «»2013 г. Зав.каф. Пиралишвили Ш.А. | |
Лаборатория «Физические основы механики»
ЛАБОРАТОРНАЯ РАБОТА № ФМ-1
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА
МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
| Переработано: к.т.н., доцент | |
| Каляева Н.А. _________ | |
| Рецензент: к.п.н., доцент Попкова Е. А. _________ |
Рыбинск 2013
ТРЕБОВАНИЯ ТЕХНИКИ БЕЗОПАСНОСТИ: необходимо выполнение общих требований безопасности, установленных в лаборатории.
ЦЕЛЬ РАБОТЫ: изучение вращательного движения тела на примере крутильных колебаний. Определение момента инерции твердого тела.
1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Абсолютно твёрдым телом называется тело, которое ни при каких условиях не может деформироваться, то есть расстояние между двумя точками (или точнее между двумя частицами) этого тела остаётся постоянным.
При вращении твёрдого тела все его точки движутся по окружности, центры которых лежат на одной прямой, называемой осью вращения. Окружности, по которым движутся точки тела, лежат в плоскостях, перпендикулярных к этой оси.
1.1 КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
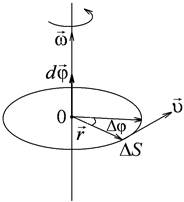 Рис. 1.1.1 Рис. 1.1.1 |
Пусть некоторая точка движется по окружности радиуса r (рис. 1.1.1). Её положение через промежуток времени 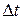 зададим углом
зададим углом 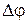 . Элементарные (бесконечно малые) углы поворота рассматриваются как векторы. Модуль вектора
. Элементарные (бесконечно малые) углы поворота рассматриваются как векторы. Модуль вектора 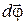 равен углу поворота, а его направление определяется по правилу правого винта (рис.1.1.1).
равен углу поворота, а его направление определяется по правилу правого винта (рис.1.1.1).
Векторы, направления которых связываются с направлением вращения твёрдого тела, называются псевдовекторами или аксиальными векторами. Эти векторы не имеют определённых точек приложения: они могут откладываться из любой точки оси вращения.
Быстроту вращения характеризует угловая скорость. Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени: 
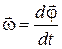 .
.
Вектор 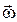 направлен вдоль оси вращения в соответствии с правилом правого винта, т.е. так же, как и вектор
направлен вдоль оси вращения в соответствии с правилом правого винта, т.е. так же, как и вектор 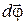 (рис. 1.1.1). Единицей угловой скорости служит радиан в секунду (рад/с).
(рис. 1.1.1). Единицей угловой скорости служит радиан в секунду (рад/с).
Величина линейная скорости точки (рис. 1.1.1):

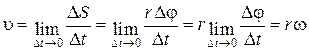 .
.
Направлена линейная скорость 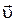 по касательной к траектории.
по касательной к траектории.
В векторном виде формулу для линейной скорости можно написать как векторное произведение угловой скорости 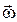 и радиус-вектора
и радиус-вектора 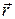 , проведённого из центра окружности в рассматриваемую точку (рис.1.1.1):
, проведённого из центра окружности в рассматриваемую точку (рис.1.1.1):
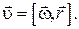
Если 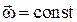 , то вращение называется равномерным и его можно характеризовать периодом вращения
, то вращение называется равномерным и его можно характеризовать периодом вращения 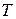 – временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол
– временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 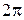 . Так как промежутку времени
. Так как промежутку времени 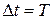 соответствует угол
соответствует угол 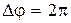 , то
, то
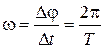 , откуда
, откуда 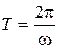 .
.
Число полных оборотов, совершаемых телом при равномерном его движении по окружности в единицу времени, называется частотой вращения:
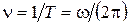 , откуда
, откуда 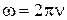 .
.
Быстроту изменения угловой скорости характеризует угловое ускорение – векторная величина, равная первой производной угловой скорости по времени или второй производной от угла поворота по времени:
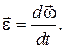
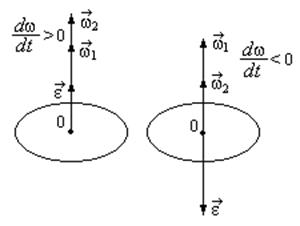 Рис. 1.1.2 Рис. 1.1.2 |
Модуль углового ускорения равен: 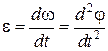 .
.
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор 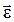 сонаправлен вектору
сонаправлен вектору 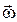 , при замедленном – противонаправлен ему (рис. 1.1.2).
, при замедленном – противонаправлен ему (рис. 1.1.2).
Ускорение 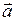 производной точки твердого тела, вращающегося вокруг неподвижной точки О или неподвижной оси, проходящей через эту точку, называют линейным ускорением. Оно равно:
производной точки твердого тела, вращающегося вокруг неподвижной точки О или неподвижной оси, проходящей через эту точку, называют линейным ускорением. Оно равно:
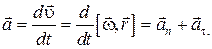
где 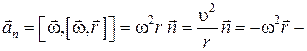 нормальное или центростремительное ускорение;
нормальное или центростремительное ускорение; 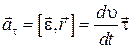 - касательное или тангенциальное ускорение. Здесь
- касательное или тангенциальное ускорение. Здесь 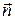 - единичный вектор, направленный по нормали в данной точке траектории;
- единичный вектор, направленный по нормали в данной точке траектории; 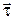 - единичный вектор, направленный по касательной к траектории в направлении скорости
- единичный вектор, направленный по касательной к траектории в направлении скорости 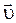 точки (рис.1.1.3).
точки (рис.1.1.3).
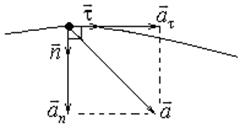 Рис. 1.1.3 Рис. 1.1.3 |
Нормальное ускорение 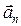 характеризует быстроту изменения направления вектора скорости точки, оно направленно по нормали к траектории к центру кривизны. Величина нормального ускорения
характеризует быстроту изменения направления вектора скорости точки, оно направленно по нормали к траектории к центру кривизны. Величина нормального ускорения 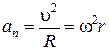 , где
, где 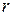 - радиус кривизны траектории в данной точке.
- радиус кривизны траектории в данной точке.
Касательное ускорение 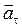 характеризует быстроту изменения модуля скорости, оно направленно по касательной к траектории. Векторы
характеризует быстроту изменения модуля скорости, оно направленно по касательной к траектории. Векторы 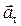 и
и 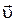 совпадают по направлению, т.е
совпадают по направлению, т.е 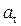 >0, при ускоренном движении точки; векторы
>0, при ускоренном движении точки; векторы 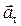 и
и 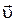 взаимно противоположны по направлению, т.е
взаимно противоположны по направлению, т.е 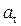 <0 при замедленном движении точки, и
<0 при замедленном движении точки, и 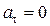 при ее равномерном движении. Величина касательного ускорения
при ее равномерном движении. Величина касательного ускорения 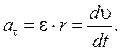
Учитывая, что векторы 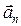 и
и 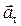 взаимно перпендикулярны, величина полного линейного ускорения
взаимно перпендикулярны, величина полного линейного ускорения 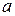 будет определяться по теореме Пифагора:
будет определяться по теореме Пифагора:
.
Таким образом, связь между линейными (длина пути S, пройденного точкой по дуге окружности радиуса 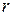 ; линейная скорость
; линейная скорость 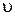 ; тангенциальное ускорение
; тангенциальное ускорение 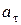 ; нормальное ускорение
; нормальное ускорение 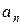 ) и угловыми величинами (угол поворота
) и угловыми величинами (угол поворота 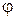 , угловая скорость
, угловая скорость 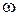 , угловое ускорение
, угловое ускорение 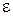 ) выражается следующими формулами:
) выражается следующими формулами:
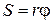 ,
, 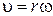 ,
, 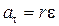 ,
, 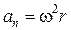 .
.
В случае равнопеременного движения точки по окружности ( 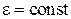 ):
):
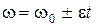 ;
; 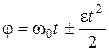 ,
,
где 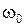 – начальная угловая скорость; знак «+» соответствует равноускоренному вращательному движению, знак «–» – равнозамедленному вращательному движению.
– начальная угловая скорость; знак «+» соответствует равноускоренному вращательному движению, знак «–» – равнозамедленному вращательному движению.
1.2 МОМЕНТ ИНЕРЦИИ
Моментом инерции системы (тела) относительно оси вращения называется скалярная физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:
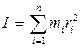 .
.
В случае непрерывного распределения масс эта сумма сводится к интегралу:
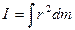 ,
,
где интегрирование производится по всему объёму тела. Величина 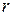 в этом случае есть функция положения точки с координатами x, y, z.
в этом случае есть функция положения точки с координатами x, y, z.
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела I относительно любойоси вращения равен моменту его инерции 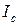 относительно параллельной оси, проходящей через центр масс C тела, сложенному с произведением массы m тела на квадрат расстояния d между осями:
относительно параллельной оси, проходящей через центр масс C тела, сложенному с произведением массы m тела на квадрат расстояния d между осями:
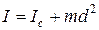 .
.
В таблице 1.2.1 приведены значения моментов инерции для некоторых тел (тела считаются однородными, m – масса тела).
| Тело | Положение оси вращения | Момент инерции |
| Полый тонкостенный цилиндр, обруч радиусом R | Ось симметрии | 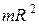 |
| Сплошной цилиндр (диск) радиусом R | Ось симметрии | 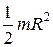 |
Прямой тонкий стержень длиной 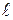 | Ось перпендикулярна стержню и проходит через его середину | 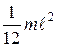 |
| Ось перпендикулярна стержню и проходит через его конец | 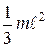 | |
| Шар радиусом R | Ось проходит через центр шара | 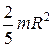 |
Таблица 1.2.1
Если тело имеет сложную форму, и теоретически определить момент инерции его сложно, прибегают к экспериментальным методам определения момента инерции.
1.3 КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩЕНИЯ
Рассмотрим абсолютно твёрдое тело, вращающееся около неподвижной оси z, проходящей через него (рис. 1.3.1). Мысленно разобьём это тело на маленькие объёмы с элементарными массами 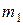 ,
, 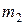 ,...,
,..., 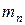 , находящиеся на расстоянии
, находящиеся на расстоянии 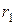 ,
, 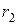 ,...,
,..., 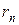 от оси вращения. При вращении твёрдого тела относительно неподвижной оси отдельные его элементарные объёмы массами
от оси вращения. При вращении твёрдого тела относительно неподвижной оси отдельные его элементарные объёмы массами 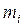 опишут окружности различных радиусов
опишут окружности различных радиусов 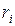 и имеют различные линейные скорости
и имеют различные линейные скорости 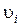 . Но так как мы рассматриваем абсолютно твёрдое тело, то угловая скорость вращения этих объёмов одинакова:
. Но так как мы рассматриваем абсолютно твёрдое тело, то угловая скорость вращения этих объёмов одинакова:
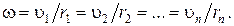 (1.3.1)
(1.3.1)
Кинетическую энергию вращающегося тела найдём как сумму кинетических энергий его элементарных объёмов:
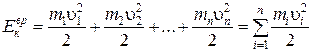 .
.
Используя выражение (1.3.1), получим:
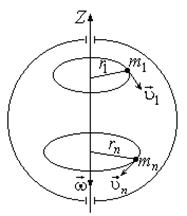 Рис. 1.3.1 Рис. 1.3.1 |
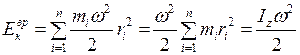 , (1.3.2)
, (1.3.2)
где 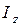 – момент инерции тела относительно оси z.
– момент инерции тела относительно оси z.
Из сравнения формулы (1.3.2) с выражением для кинетической энергии тела, движущегося поступательно 
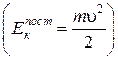 , следует, что момент инерции I вращательного движения – мера инертности тела во вращательном движении, т.е. является вращательным аналогом массы.
, следует, что момент инерции I вращательного движения – мера инертности тела во вращательном движении, т.е. является вращательным аналогом массы.
В случае, когда тело совершает одновременно поступательное и вращательное движение (например, шар катится по плоскости), его кинетическая энергия равна сумме кинетических энергий поступательного и вращательного движений:
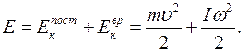

1.4 МОМЕНТ СИЛЫ. ОСНОВНОЙ ЗАКОН ДИНАМИКИ
