Изучение основной тенденции развития

Особый интерес в исследовании закономерностей динамических процессов представляет выявление общей тенденции развития (тренда). При изучении основной тенденции ряда динамики решаются две взаимосвязанные задачи:

1) выявление основной тенденции развития и описание его качественных особенностей;

2) измерение выявленного тренда, т.е. получение обобщающей количественной оценки основной тенденции развития.

Эти задачи решаются с помощью различных методов анализа рядов динамики. К ним относятся:

1. Метод укрупнения интервалов – применяется для выявления тренда в рядах динамики колеблющихся уровней, затушевывающих основную тенденцию развития. При этом первоначальный ряд динамики преобразуется в ряд с более продолжительными периодами (месячные периоды в квартальные, квартальные в годовые и т.д.).

2. Метод скользящей средней.

С его помощью от исходных данных переходят к теоретическим уровням, в которых случайные колебания погашаются, а основная тенденция развития выражается в виде плавной линии.

Скользящая средняя - это подвижная динамическая средняя, образованная из определенного числа уровней ряда при последовательном передвижении на один уровень. Применение способа укрупнения интервалов, расчет скользящих средних позволяет установить закономерность изменения ряда динамики.

3. Приведение рядов динамики к одному основанию.

Метод применяется при сравнительном анализе тенденций развития взаимосвязанных явлений. Проведение такого анализа значительно облегчается, если рассматриваемые динамические ряды приведены к одному основанию, то есть выражают уровни сравниваемых рядов в процентах по отношению к начальному, среднему или иному характерному уровню динамического ряда.

В связи с тем, что база сравнения (основание) оказывает существенное влияние на величины относительных показателей динамики, в процессе статистического анализа ему следует уделять необходимое внимание. Обычно выбору основания предшествует периодизация динамики, то есть расчленение динамических рядов на однокачественные периоды или этапы развития явлений.

4. Метод аналитического выравнивания

С его помощью решается задача измерения тренда.

Основным содержанием метода аналитического выравнивания в рядах динамики является то, что основная тенденция развития Yt рассчитывается как функция времени:

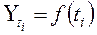, (7.23)

Определение расчетных (теоретических) уровней Yt производится на основе адекватной математической функции, наилучшим образом отображающей основную тенденцию ряда динамики. Подбор функции осуществляется методом наименьших квадратов, суть которого состоит в том, что эмпирические уровни динамического ряда Yi заменяются плавной линией выравненных уровней Yti таким образом, чтобы сумма этих отклонений была равна 0, а сумма квадратов отклонений была минимальной:

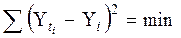, (7.24)

Аналитическое выравнивание по прямой линии производится в том случае, если наблюдается равномерный абсолютный прирост. Уравнение прямой имеет вид:

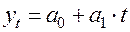, (7.25)

где Yt - расчетные уровни динамического ряда;

t - порядковый номер времени;

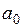- свободный параметр уравнения;

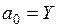, если t=0;

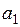- параметр динамики, показывающий, как в среднем изменится Y, если t увеличится на единицу.

Для определения параметров a₀ и a₁ необходимо решить систему нормальных уравнений:

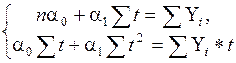, (7.26)

Если значения t подобрать так, чтобы их сумма равнялась 0, то решение системы можно упростить. Параметры уравнения при этом можно рассчитать следующим образом:

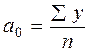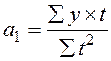, , (7.27, 7.28)

Если явление изменяется в геометрической прогрессии, то выравнивание производится по показательной кривой:

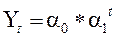, (7.29)

Если наблюдается равномерное ускорение, то выравнивание производится по параболе второго порядка:

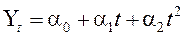, (7.30)

Часто для уравнения тренда подходят одновременно несколько функций. Отбор оптимальной производится по величине стандартизированной ошибки аппроксимации, которая вычисляется по формуле:

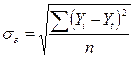, (7.31)