Формулы полной вероятности и Байеса
Задача. В первой урне находится 1 белый и 9 черных шаров, а во второй - 5 белых и 1 черный. Из каждой урны наугад вынули по одному шару, а остальные ссыпали в третью урну, из которой извлекли один шар. Найти вероятность того, что:
- из третьей урны вынут белый шар;
- из обеих урн вынули белые шары, если из третьей урны извлекли
белый шар.
Сообразно постановке задачи введем обозначения событий, фигурирующих в ней непосредственно, а также событий, отвечающих всевозможным сценариям объединения урн: А=”из третьей урны извлечен белый шар”;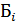 
и 
- и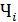з 𝑖 -й урны (𝑖=1,2) извлечены соответственно белый и черный шар. Теперь следуя логике решения первой части задачи, изобразим дерево вероятностей с учетом всех возможных исходов при проведении трех шагового мысленного эксперимента: вынули шар из первой урны, вынули шар из второй урны, вынули шар из третьей ур-
ны. Этим опытам будет отвечать четырехуровневое дерево вероятностей, каждой ветви которого соответствует свой сценарий эксперимента с учетом всех возможных вариантов выбора шаров.
| Из У1 вынут |
Р(  )=  |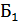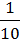
Р(  )=  |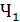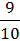
| Белый шар |
| Из У2 вынут |
| Черный шар |
| Из У2 вынут |
Р(  )=  |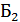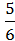
Р(  )=  |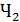
| Белый шар |
| Из У3 вынут |
| Черный шар |
| Из У3 вынут |
| Белый шар |
 =  |
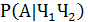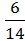| Белый шар |
 =  |
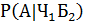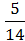| Р( )= |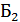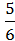
| Р( )= |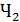
| Белый шар |
| Из У3 вынут |
| Черный шар |
| Из У3 вынут |
| Белый шар |
 = |
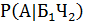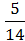| Белый шар |
 =  |
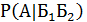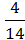В этой схеме итоговые условные вероятности посчитаны исходя из наличного количества белых и черных шаров, отвечающего развитию начальной ситуации по тому или иному сценарию.
В качестве гипотез примем всевозможные комбинации выбора шаров, подсказанные деревом вероятностей: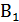 
= 
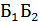(из обеих урн вынули по белому шару), 
= 
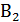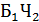(из первой - белый из второй - черный), 
= 
, 
= 
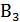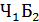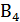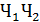. Эти гипотезы сформированы как произведения независимых событий и сами являются независимыми и попарно несовместными событиями, образующими полный набор, т.е. непременно происходит одно из 
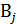, 𝑗=1, 2, 3, 4 и А содержится в их сумме. Таким образом, удовлетворены условия применимости формулы полной вероятности
Р(А) =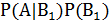 
+ 
+ 
+ 
.
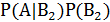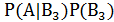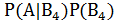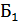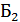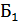В силу независимости событий 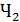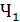и , и 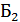, 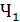и , и 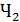имеем
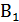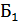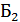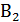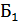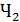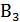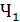Р( )= Р( )Р( ), Р( )= Р( )Р( 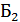), Р( )= Р( 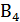)Р( ), Р( 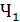)= Р( )Р( ).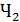
Подставляя сюда численные значения нашей задачи, получаем
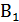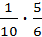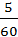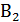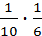Р( )= 
= 
, Р( )=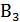 
= 
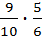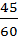, Р( )= 
= 
, Р( )=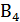 
= 
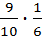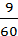
и, взяв с дерева вероятностей значения условных вероятностей события А относительно принятых гипотез, окончательно находим решение первой части задачи
Р(А) =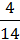 
· 
+ 
· 
+ · 
+ · 
= 
= 
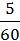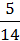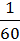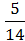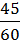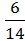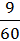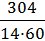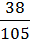≈ 0.36 = 36%.
Ответ на вторую часть задачи (вероятность гипотезы 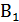) дает формула Байеса
= 
= 
= 
= 
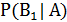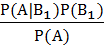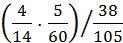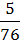≈ 0.066.
Посчитаем вероятности развития событий по остальным ветвям дерева вероятностей:
= 
= 
= 
= 
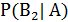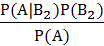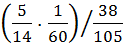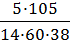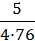≈ 0.016,
= 
= 
= 
= 
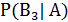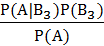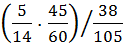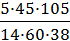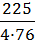≈ 0.740,
= 
= 
= 
= 
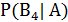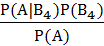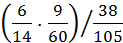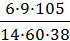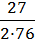≈ 0.178.
Таким образом, наиболее вероятной является третья сверху ветвь дерева вероятностей, хотя априори, казалось бы, таковой должна быть самая нижняя ветвь, сохраняющая в урнах все белые шары и тем самым повышающая вероятность извлечь белый шар из третьей урны. Это обстоятельство лишний раз подчеркивает неочевидность выводов.
Нетрудно проверить, что
+ 
+ 
+ 
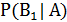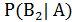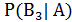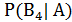=1.
Это не случайно, а является очевидным следствием полноты набора гипотез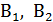 
, 
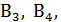для которого 
+ 
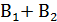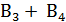=Ω, и свойств условной вероятности относительно суммы несовместных событий и достоверного события
+ 
+ 
+ 
= 
= 
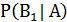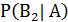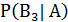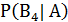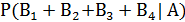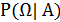=1.