Векторы, операции над векторами. Скалярное, векторное, смешанное произведения векторов

[2], гл.1; [8], гл.2; [10]

При решении задач на эту тему необходимо знать определения скалярного, векторного и смешанного произведений векторов, уметь вычислять и применять эти произведения. Скалярным произведением векторов 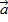и называется число

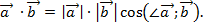
Зная координаты перемножаемых векторов

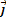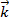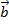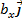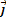а = а_х + a_y + a_z =(a_x;a_y ;a_z); = + b_y + b_z 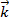=(b_x;b_y;b_z), можно вычислить скалярное произведение a·b=a_xb_x+a_yb_y+a_zb_z. Условием ортогональности (перпендикулярности) векторов а и b является равенство нулю их скалярного произведения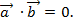

Векторным произведением вектора 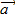на вектор 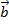называется вектор 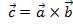, который

1) перпендикулярен векторам 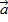и ,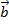

2) образует с ними правую тройку , , и

3) длина которого равна площади параллелограмма, построенного на векторах а и В, как на сторонах, т.е. 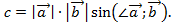Если известны координаты перемножаемых векторов, то векторное произведение 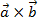вычисляется по формуле:

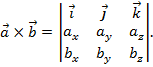
Смешанное произведение векторов 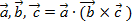есть скалярное произведение вектора 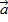на векторное произведение 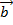и 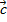и вычисляется по формуле:

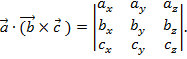
Абсолютная величина смешанного произведения векторов 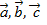равна объему параллелепипеда, построенного на этих векторах.

Если 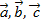-правая тройка векторов, то 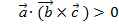, если левая, то 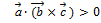; 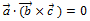–условие компланарности трех векторов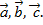

Пример 4.На векторах 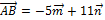и 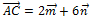построен треугольник ABC. Найти площадь треугольника ABC и его высоту, опущенную на сторону ВС, если длины векторов 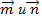равны соответственно 1 и 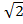, а угол, образованный векторами 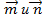, равен 135°.

Решение:1) Найдем площадь S треугольника ABC. Площадь треугольника, построенного на векторах, равна половине модуля их векторного произведения, то есть

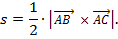
Вычислим векторное произведение векторов 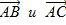. Для этого применим распределительное свойство векторного произведения:

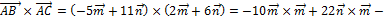30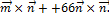

Векторное произведение вектора самого на себя равно нулевому вектору, следовательно 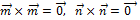; при перестановке сомножителей векторное произведение меняет знак на противоположный, значит 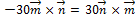. Отсюда,

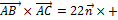30 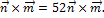Находим модуль полученного вектора

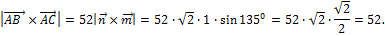
Следовательно,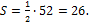

2) Найдем сторону ВС треугольника АВС, то есть длину вектора 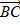. Согласно правилу треугольника сложения векторов, 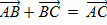, откуда

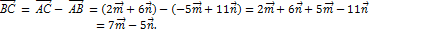
Найдем длину полученного вектора по формуле: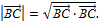

Над корнем стоит скалярное произведение вектора 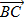самого на себя. Найдем его

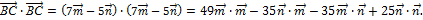
С учетом того, что 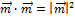, , 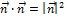, 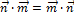получаем

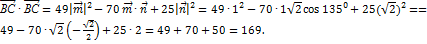
3) Найдем высоту h треугольника ABC, опущенную на сторону ВС. По формуле площади треугольника имеем 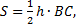откуда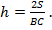

Площадь треугольника S и сторона ВС найдены ранее: S = 26, ВС =13. Следовательно,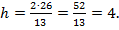

4.1.4. Приложение векторной алгебры к задачам аналитической геометрии[2],гл.2,3; [8],гл.3,§1

Задачи на прямую и плоскость в пространстве рекомендуется решать средствами векторной алгебры. При решении задач необходимо уметь использовать различные формы уравнений прямых и плоскостей, а также умен, переходить от одной формы уравнения к другой.

Задачи на прямую и плоскость в пространстве, рекомендуется решать средствами векторной алгебры. При решении задач необходимо уметь использовать различные формы уравнений прямых и плоскостей, а также уметь переходить от одной формы уравнения к

Пример 5. Составить уравнение плоскости, проходящей через точки M₁(1,-2,3),M₂(2,-1,0) и точку пересечения прямой 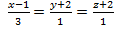с плоскостью xOy.

Решение: Найдём координаты точки М₃(х,у,z) - точки пересечения заданной прямой с плоскостью хОу. Для этого от канонических уравнений прямой перейдем к параметрическим и, добавив уравнение плоскости хОу z =0, получим систему для определения координат искомой точки:

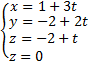
Из третьего и четвертого уравнений получим t = 2, тогда х = 7; у = 2; 2 = 0. Таким образом, М₃(7,2,0) - точка пересечения, заданной прямой с плоскостью хОу.

Составим уравнение плоскости, проходящей через точки М₁,М₂,М₃, Если точка М (х,у,z) - текущая точка плоскости, то векторы 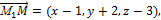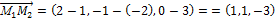и 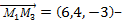компланарны, следовательно, их смешанное произведение равно нулю: 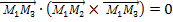или в координатной форме

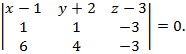
Раскрыв этот определитель по элементам первой строки, получим уравнение искомой плоскости:

9(х-1)-15(у + 2)-2(z-3) = 0 или 9х-15у – 2z - 33 = 0.

Пример 6. Найти уравнение плоскости, проходящей через точку A(2;-1;1) и прямую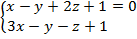

Решение: Приведем общие уравнения прямой к каноническому виду 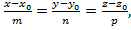где 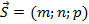– направляющий вектор прямой, а 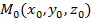– точка, лежащая на этой прямой. Так как прямая лежит в обеих данных плоскостях, в плоскости х - у + 22z + 1 = 0 и в плоскости 3х - у - 2 + 1 =0, то ее направляющий вектор 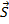перпендикулярен нормальным векторам этих плоскостей N₁ = (1; -1;2) и N₂= (3; -1; -1), поэтому можно выбрать

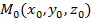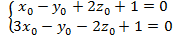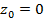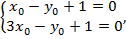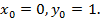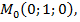
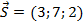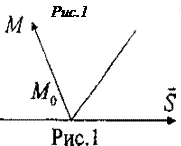
Координаты точки найдем из системы уравнений, задающих прямую . Выбирая одну из координат произвольно, например, положим получим, откуда Значит, канонические уравнения прямой имеют вид: 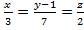Теперь найдем уравнение плоскости, проходящей через прямую и точку А.

Выберем произвольную точку искомой плоскости М(х,у,z), тогда три вектора 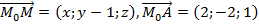компланарны, (см.рис.1), значит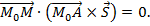

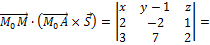
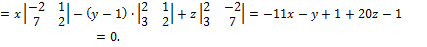
Т. о. уравнение искомой плоскости 11х + у – 20z -1=0.