Дифференциальные уравнения фильтрации
Основные понятия и определения
Фильтрацией называется движение жидкостей, газов, их смесей в пористых и трещиноватых средах, то есть в твердых телах, пронизанных системой сообщающихся между собой пор и микротрещин. Фильтрация жидкостей и газов по сравнению с движением в трубах и каналах обладает некоторыми специфическими особенностями: происходит по чрезвычайно малым в поперечных размерах поровым каналам при очень малых скоростях движения жидкостей; силы трения при движении жидкости в пористой среде очень велики, так как площади соприкосновения жидкости с твердыми частицами огромны.
Коэффициентом пористости m называется отношение объема пор в образце Vпор к объему образца V:
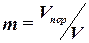 . . | (1.1) |
Под пористостью понимается активная пористость, которая учитывает только те поры и микротрещины, которые соединены между собой и через которые может фильтроваться жидкость.
Коэффициентом просветности n называется отношение площади просветов wпр в данном сечении пористой среды ко всей площади этого сечения w:
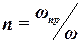 . . | (1.2) |
Площадь просветов различна в различных поперечных сечениях wпр(х). Среднее значение просветности по длине образца равно пористости:
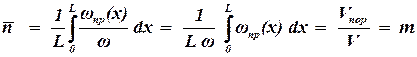 . . | (1.3) |
Поперечным сечением w называется поверхность, проведенная перпендикулярно направлению скорости.
Объемным расходом Q называется объем жидкости, прошедший через поперечное сечение за единицу времени:
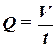 . . | (1.4) |
Массовым расходом Qm называется масса жидкости, прошедшая через поперечное сечение за единицу времени:
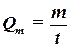 . . | (1.5) |
Массовый расход равен произведению плотности r на объемный расход:
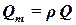 . . | (1.6) |
Скоростью фильтрации u называется отношение объемного расхода жидкости к площади поперечного сечения:
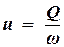 . . | (1.7) |
Скорость фильтрации ‑ это скорость, с которой двигалась бы жидкость, если бы пористая среда отсутствовала (m = 1).
В действительности фильтрация жидкости или газа происходит по просветам, поэтому действительная скорость v больше скорости фильтрации и определяется:
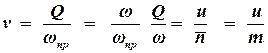 . . | (1.8) |
При плоскопараллельном потоке векторы скоростей параллельны друг другу, поэтому фильтрация происходит только вдоль одной оси, которую можно принять за ось x. В любом поперечном сечения плоскопараллельного потока давление, скорость и её направление одинаковы, но в разных поперечных сечениях они разные и являются функцией координаты этой оси p(x), u(x). Плоскопараллельное движение имеет место в двух следующих случаях.
1. В лабораторных условиях при фильтрации через цилиндрический керн, или в трубе диаметром D, заполненной пористой средой (рисунок 1.1). Площадь поперечного сечения представляет собой площадь круга и равна:
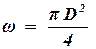 . . | (1.9) |
2. На некоторых участках продуктивного пласта, которые можно представить в виде параллелепипеда, верхние и нижние грани (кровля и подошва пласта), а также ближняя и дальняя грань ‑ непроницаемы для жидкости. Во всех точках левой грани поддерживается постоянное давление pк, а во всех точках правой грани поддерживается постоянное давление pг. Расстояние между кровлей и подошвой пласта называется толщиной пласта и обозначается h. Расстояние между ближней и дальней гранью называется шириной и обозначается B. Расстояние между левой и правой гранью называется длиной и обозначается L. Этот случай плоскопараллельного движения часто называют галереей, а величины h, B и L называют толщиной, шириной и длиной галереи.
Модель пласта | |||
Галерея | |||
| Рисунок 1.1 ‑ Плоскопараллельный поток |
Площадь поперечного сечения галереи равна:
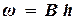 . . | (1.10) |
При плоскорадиальном потоке в любой горизонтальной плоскости продолжения векторов скоростей сходятся (или расходятся) в одной точке (рисунок 1.2). На практике плоскорадиальной поток встречается в случае вскрытия горизонтального пласта вертикальной скважиной с круговым контуром питания. Если вскрыт весь пласт и приток происходит по всей боковой поверхности скважины, то скважина называется гидродинамически совершенной. Расстояние от оси скважины до какой – либо точки пласта называется радиусом r. Площадь поперечного сечения представляет собой боковую поверхность цилиндра, высота которого равна толщине пласта h, а радиус – расстоянию от центра скважины до данной точки пласта:
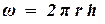 . . | (1.11) |
В любом поперечном сечении этого потока давление и скорость одинаковы, но в разных поперечных сечениях они разные и являются функцией радиуса p(r), u(r).
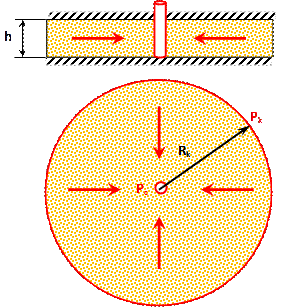 Рисунок 1.2 – Плоскорадиальный поток Рисунок 1.2 – Плоскорадиальный поток |
При радиально-сферическом потоке продолжения векторов скоростей в пространстве сходятся (или расходятся) в одной точке (рисунок 1.3). Расстояние от этой точки, которую называют источником или стоком, до любой точки пласта называется радиусом r. Площадь поперечного сечения представляет собой поверхность сферы радиусом r:
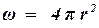 . . | (1.12) |
В любом поперечном сечении этого потока давление и скорость одинаковы, но в разных поперечных сечениях они разные и являются функцией радиуса p(r), u(r).
Рисунок 1.3 – Радиально-сферический поток 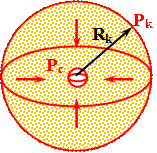 |
На практике радиально–сферическийпоток встречается в случае вскрытия скважиной кровли пласта бесконечно большой толщины скважиной с полусферическим контуром питания.
В общем случае давления и скорости фильтрации зависят от координаты точки и времени:
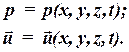 | (1.13) |
Движение называется установившимся (стационарным), если в любой точке пласта давления и скорости фильтрации не зависят от времени. В противном случае движение называется неустановившимся (нестационарным).
Закон Дарси
Движение однородной жидкости в пористой среде определяется силами давления и силами тяжести. Основное соотношение теории фильтрации – закон Дарси – устанавливает связь между величиной скорости фильтрации вдоль линии тока и силами, действующими в жидкости.
Рассмотрим вывод закона Дарси на примере схемы опытной установки (рисунок 1.4). Пусть по трубе, диаметром D и длиной L, заполненной пористой средой, фильтруется жидкость со скоростью u. Выберем два поперечных сечения: 1 и 2. Центры тяжести поперечных сечений расположены на высотах z1 и z2. Давление p1 и p2 в сечениях замеряем пьезометрами. Как и в трубной гидравлике запишем уравнение Бернулли для этих сечений:
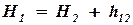 , , | (1.14) |
где 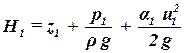 – гидродинамический напор;
– гидродинамический напор;
h12 = h(u) – потери напора между сечениями, которые зависят от скорости фильтрации и не могут рассчитываться по формулам трубной гидравлики.
Скорости фильтрации жидкости в пористой среде малы, поэтому скоростным напором можно пренебречь. Разрешая уравнение (1.14) относительно скорости фильтрации, получим:
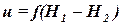 . . | (1.15) |
Рассмотрим зависимость скорости фильтрации от расстояния между сечениями и площади поперечного сечения. При прочих равных условиях с увеличением расстояния увеличиваются сопротивления движению жидкости и скорость фильтрации должна уменьшатся. Наиболее простая зависимость – обратно пропорциональная u ~ 1/L.
Предположим, что скорость фильтрации зависит от площади поперечного сечения, тогда во всем образце она будет одиаковая. Проделаем мысленный эксперимент. Разделим поперечное сечение пополам и рассмотрим одну половину. Площадь поперечного сечения изменилась, значит должна измениться и скорость, но в одном и том же реальном образце не могут быть две различные скорости фильтрации. Поэтому наше предположение не верно, и скорость фильтрации не зависит от площади. Кроме того, скорость фильтрации зависит от свойств фильтрующейся жидкости и свойств пористой среды. Учтем эти свойства коэффициентом фильтрации – kф.
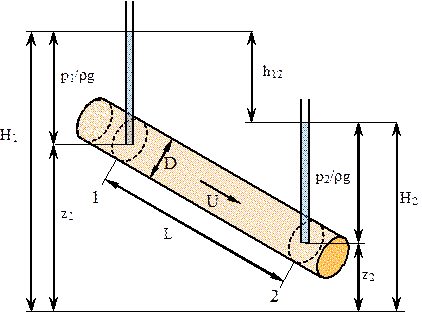 Рисунок 1.4 – Схема опытной установки Рисунок 1.4 – Схема опытной установки |
Тогда формула (1.15) запишется так:
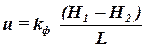 . . | (1.16) |
Эта формула впервые была экспериментально получена французским инженером Дарси и подтверждается для многих жидкостей и газов в широких пределах изменения скоростей. Но для некоторых жидкостей и значений скоростей фильтрации эта формула не подтверждается. Коэффициент фильтрации kф используется в тех случаях, когда фильтруется вода. При фильтрации нефти, газа, воды, их смесей желательно учитывать свойства породы и жидкости отдельно. Свойства жидкости характеризуются коэффициентом динамической вязкости μ и плотностью r, тогда коэффициент фильтрации можно записать в виде:
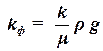 , , | (1.17) |
где k – коэффициент проницаемости пористой среды, м2;
m – коэффициент динамической вязкости жидкости, Па×с;
r – плотность жидкости, кг/м3;
g – ускорение свободного падения, м/с2.
Коэффициент проницаемости зависит только от свойств пористой среды и определяет способность пористой среды пропускать сквозь себя жидкости и газы. Коэффициент проницаемости имеет размерность площади (в СИ [k] = м2 = 10 12 мкм2) и качественно представляет собой площадь поперечного сечения отдельного капилляра, поэтому проницаемость горных пород очень мала.
Например: проницаемость крупнозернистых песчаников, а таких нефтяных или газовых пластов составляет 10-12 – 10-15 м2. На практике до сих пор проницаемость измеряется устаревшими единицами, называемыми Дарси (Д или Дарси). С введением системы единиц СИ использовать эту единицу запрещено. Для перевода в систему СИ используется соотношение 1 Дарси = 1,02 10-12 м2 = 1,02 мкм2.
Коэффициент динамической вязкости жидкости зависит только от свойств жидкости и имеет размерность: Па×с = кг/м×с. Для большинства реальных жидкостей 1 Па×с величина большая, поэтому используется более мелкая единица 1 мПа×с = 10-3 Па×с.
Вязкость воды при температуре 20 С° равна 1 мПа×с. Вязкость нефти в пластовых условиях меняется в очень широком диапазоне: она может быть меньше вязкости воды при температуре 20 С°, а может быть в десятки или сотни раз больше. Вязкость Ярегской нефти равна 5000 мПа×с, а вязкость нефти пермокарбоновой залежи Усинского месторождения = 10000 мПа×с. Вязкость нефти очень сильно зависит от температуры. В среднем при её увеличении на 10 С° вязкость уменьшается в два раза. Это является основой при использовании тепловых методов разработки месторождений. Вязкость газов зависит от состава газа и ориентировочно равна 0,02 мПа×с.
С введение коэффициента проницаемости закон Дарси примет вид:
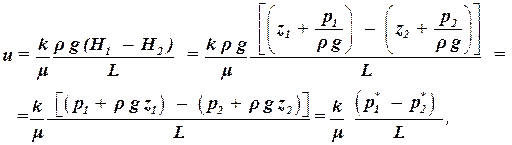 | (1.18) |
где p* = p + r g z – приведенное давление.
Расстояния z от плоскости сравнения до данной точки считается положительным, если точка лежит выше плоскости сравнения, и отрицательной, если ниже. За плоскость сравнения можно принять любую горизонтальную плоскость. Обычно принимают границу газонефтяного (ГНК) или водонефтяного (ВНК) контакта. При движении жидкости в горизонтальных пластах (z = const), значит, второе слагаемое в приведенном давлении постоянно и при подстановке в формулу обращается в нуль. Поэтому в горизонтальных пластах при движении однородной жидкости приведенное давление можно положить равным давлению в данной точке и символ (*) в законе Дарси можно опустить.
Рассмотрим трубку тока, вдоль которой происходит фильтрация жидкости. Обозначим расстояние вдоль вектора скорости у этой трубки через s. Выберем две точки на расстоянии Ds друг от друга и запишем для этих точек закон Дарси:
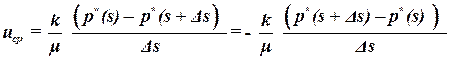 . . | (1.19) |
Получим значение средней скорости на этом участке uср. Если устремить расстояние между точками к нулю, то получим закон Дарси в дифференциальной форме:
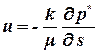 . . | (1.20) |
В векторной форме закон Дарси запишется:
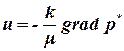 | (1.21) |
или в проекциях на оси координат
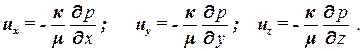 | (1.22) |
На практике проницаемость по вертикали в 2 – 10 раз меньше чем по горизонтали. Такая пористая среда называется анизотропной и закон Дарси в этом случае имеет вид:
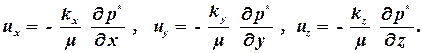 | (1.23) |
Для плоскорадиального и радиально–сферического потока Закон Дарси можно записать в виде:
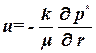 . . | (1.24) |
В пластах часто встречаются непроницаемые границы (сбросы). Жидкость двигаться перпендикулярно непроницаемой границе не может, поэтому нормальная к границе скорость равна нулю.
Тогда из закона Дарси следует:
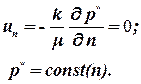 | (1.25) |
Это означает, что давление перпендикулярно непроницаемой границе не меняется и линии равного давления (изобары) перпендикулярны этой границе.


