Тәжірибелік сабақ. Анықталған интеграл

Тапсырмалар: АЖ: 7 нег. 2231,2232,2248, 2259, 2260, 2275, 2276,2455, 2458, 2521, 2522, 2556.

Әдістемелік ұсыныстар: Анықталған интегралды есептеу әдістері талқыланады. Яғни айнымалыны алмастыру және бөліктеп интегралдау әдістеріне есептер шығарылады. Үйден Ньютон-Лейбниц формуласын және анықталған интегралдың қасиеттерін қайталап келу керек. Сонымен қатар анықталған интегралдың қолданылуына есептер шығарылады.

1. 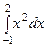интегралын есептеу керек.

Шешімі: .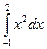

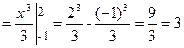2. 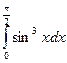интегралын есептеу керек.

Шешімі: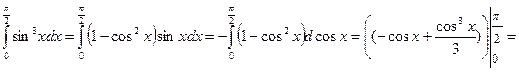

.

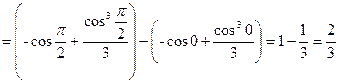3 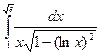интегралын есептеу керек.

Шешімі: .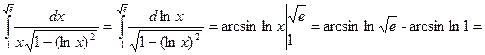

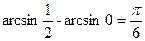4. 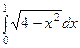интегралын есептеу керек.

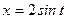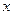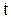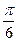Шешімі. алмастыруын енгіземіз. Егер 0 ден 1 дейін өзгерсе, онда 0 ден дейін өзгереді. 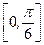кесіндісінде 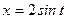функциясы бірсарынды, үзіліссіз және үзіліссіз туындысы бар функция. Анықталған интегралда айнымалыны ауыстыру ережесін қолданып берілген интегралды есептейміз.

.

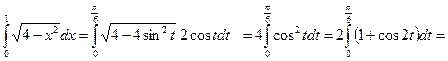
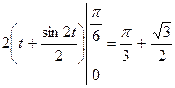5. 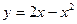парболасымен және 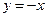түзуімен шектелген фигураның ауданын табу керек.

Шешімі.Параболаның теңдеуін қарастырайық.

.

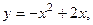
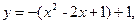
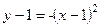Бұл параболаның төбесі (1,1)нүктесінде және ол 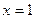түзуі бойынша симметриялы орналасқан. Берілген параболаның және түзудің чертежін салайық.

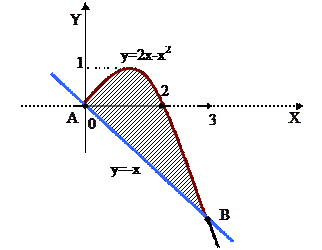
Парабола мен түзудің теңдеулерін біріктіріп шешіп мен 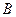нүктелерінің абсциссаларын табайық. 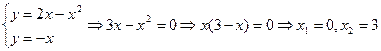. Сонда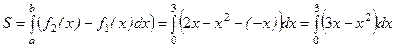

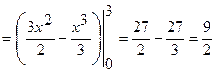
6. Мына 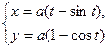циклоиданың бір доғасымен және 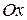өсімен шектелген фигураның ауданын табу керек.

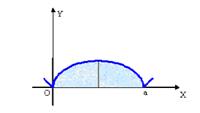
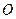және 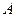нүктелері 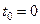және 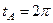параметрлерінің мәндеріне сәйкес келеді. Енді ауданды есептейміз:

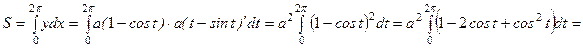
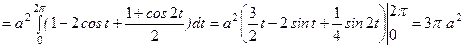(кв.ед.).

7. Мына 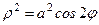қисығымен шектелген ауданды есептеңіз (Бернулли лемнискатасы).

Берілген қисықты сипаттайық. Егер 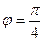болса, онда 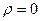, яғни қисық полюс арқылы өтеді. Қисықтың теңдеуінен 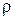полярлық радиус нақты мәндер қабылдайтынын байқауға болады.

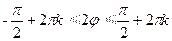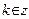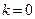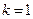, . При и имеем

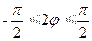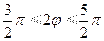, , откуда , .

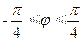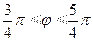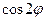функциясының периоды 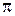-ге тең, сондықтан 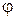-ді 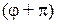ауыстырсақ 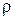-полярлық радиус өзгермейді, яғни қисық 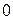-полюсі бойынша симметриялы. Сонымен қатар қисық 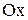полярлық өсі арқылы да симметриялы, өйткені 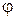-дің таңбалалары өзгерсе де 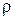-ның таңбасы өзгермейді.

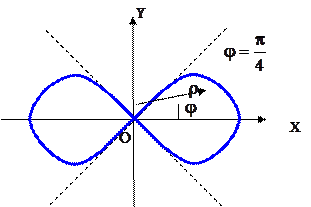
Фигураның симметриялығын ескеріп бірінші ширектегі ауданын табамыз.

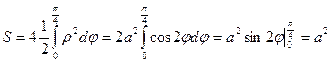(кв.ед.)

8. 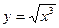қисығының координат бас нүктесінен 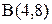нүктесінің арасындағы доғаның ұзындығын табыңыз.

Шешімі.Қисықтың теңдеуінен 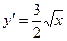табамыз. Сонда қисық доғасының ұзындығы:

.

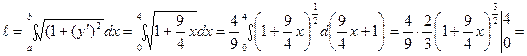
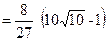9. 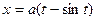, 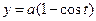циклоидасының бір иінінің доғасының ұзындығын табыңыз.

Шешімі. 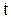параметрі 0 ден 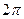дейін өзгереді, себебі нүкте дөңгелек бір айналғанда циклоиданың бір иінін сызады. Циклоиданың теңдеуінен табайық.

, ,

= .

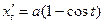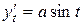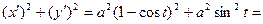
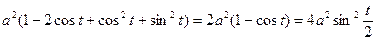Демек,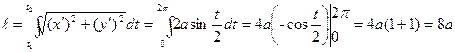

10. 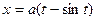, 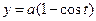циклоидасының бір доғасының (аркасының) 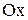осі арқылы айналуынан пайда болған дененің көлемін табайық.

Шешімі.Циклоиданыңбір доғасына 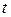параметрінің 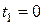ден 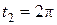дейінгі өзгеруі сәйкес келеді.

=

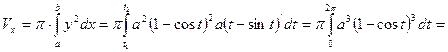
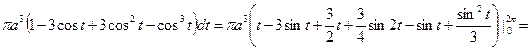
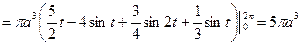
Әдебиеттер:

Негізгі: [4] 260-270 беттер; 15 қос. [243-266].

Бақылау сұрақтары:

1. Анықталған интегралдың анықтамасын беріңіз.

2. Анықталған интегралдың қасиеттерін атаңыз.

3. Анықталған интегралда айнымалыны алмастыру формуласын көрсетіңіз.

4. Жазық фигураның ауданын есептеу формулаларын көрсетіңіз.

2.4 Оқытушының жетекшілігімен орындалатын студенттердің өзіндік жұмыстары бойынша өткізілетін сабақтардың жоспары (СОӨЖ)