Тема 4. Элементы векторной алгебры
Базовый уровень
Задание {{1}} ТЗ1
Укажите формулу, по которой вычисляют скалярное произведение векторов.
R 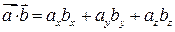
Задание {{1}} ТЗ1



 Даны векторы:
Даны векторы: 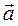 ={1,2,3} и
={1,2,3} и 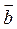 ={0,–1,3}. Координаты вектора
={0,–1,3}. Координаты вектора 
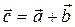 равны:
равны:
R {1,1,6}
Задание {{1}} ТЗ1
Даны векторы 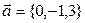 и
и 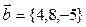 . Координаты вектора
. Координаты вектора 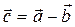 равны
равны
R {-4, -9, 8}
Средний уровень
Задание {{1}} ТЗ1
Укажите уравнение, по которому можно определить угол между векторами 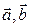 .
.
R 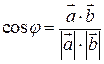
Задание {{1}} ТЗ1
Даны векторы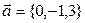 и
и 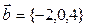 . Вектор
. Вектор 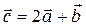 имеет координаты
имеет координаты
R {-2,-2,10}
Задание {{1}} ТЗ1
Даны векторы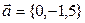 и
и 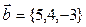 . Cкалярное произведение
. Cкалярное произведение 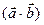 равно
равно
R –19
Задание {{1}} ТЗ1
Даны векторы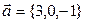 и
и 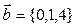 .Вектор
.Вектор 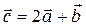 имеет координаты
имеет координаты
R {6,1,2}
Задание {{1}} ТЗ1
Дан вектор 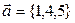 . Его модуль равен
. Его модуль равен
R 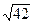
75. Задание {{1}} ТЗ1
Укажите формулу разложения вектора по ортам координатных осей.
R 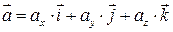
Высокий уровень
Задание {{1}} ТЗ1
Даны векторы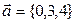 и
и 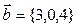 . Косинус угла между ними равен
. Косинус угла между ними равен
R 16/25
Задание {{1}} ТЗ1
Векторы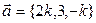 и
и 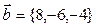 коллинеарны при k равном:
коллинеарны при k равном:
R -2
Задание {{1}} ТЗ1
Векторы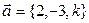 и
и 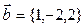 перпендикулярны при k равном
перпендикулярны при k равном
R 2
Б-базовый (3)
С-средний (6)
Т-Высокий (3)
Тема 5. Прямая на плоскости
Базовый уровень
Задание {{1}} ТЗ1
Нормальным вектором прямой линии 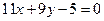 является вектор:
является вектор:
R 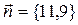
Задание {{1}} ТЗ1
Точку пересечения двух прямых линий  определяют из
определяют из
R решения системы уравнений 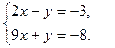
Задание {{1}} ТЗ1
Общее уравнение прямой линии в плоскости переменных 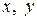 имеет вид:
имеет вид:
R 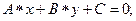
Задание {{1}} ТЗ1
Нормальным вектором прямой линии 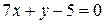 является вектор:
является вектор:
R 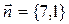
Задание {{1}} ТЗ1
Направляющим вектором прямой линии 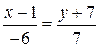 является вектор:
является вектор:
R 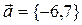
Задание {{1}} ТЗ1
Нормальным вектором прямой линии 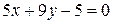 является вектор:
является вектор:
R 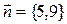
Задание {{1}} ТЗ1
Направляющим вектором прямой линии 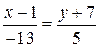 является вектор:
является вектор:
R 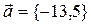
Задание {{1}} ТЗ1
Точку пересечения двух прямых линий 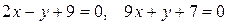 определяют из:
определяют из:
R решения системы уравнений 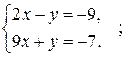
Задание {{1}} ТЗ1
Направляющим вектором прямой линии 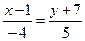 является вектор
является вектор
R 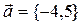
Задание {{1}} ТЗ1
Укажите формулу вычисления расстояния от точки до прямой
R 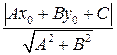
Средний уровень
Задание {{1}} ТЗ1
Прямые линии заданы уравнениями:
1) 3x–4y+5=0 2) 2x+5y–4=0 3) 6x–8y–3=0 4) 3x–5y+5=0.
Параллельными являются прямые:
R 1,3
Задание {{1}} ТЗ1
Прямые линии заданы уравнениями:
1) y=4x+1 2) y=2x–3 3) y= –x/2+4 4) y= –4х–5.
Перпендикулярными являются прямые
R 2 и 3
Задание {{1}} ТЗ1
Уравнение прямой, проходящей через точку (–11) параллельно прямой
2x – y +5=0,имеет вид
R 2x – y + 3=0
Задание {{1}} ТЗ1
Уравнение прямой, проходящей через точку (–20) перпендикулярно прямой 3x + y+ 4=0, имеет вид
R 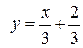
Задание {{1}} ТЗ1
Уравнение прямой, проходящей через точки М (12) и N (03), имеет вид
R 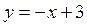
Задание {{1}} ТЗ1
Точку пересечения двух прямых линий 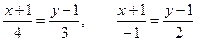 определяют из
определяют из
R решения системы уравнений 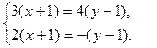
Задание {{1}} ТЗ1
Расстояние от точки 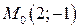 до прямой
до прямой 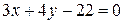 равно
равно
R 4
Высокий уровень
Задание {{1}} ТЗ1
Нормальным вектором прямой линии 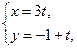 является вектор
является вектор
R 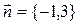
Задание {{1}} ТЗ1
Параллельным вектором к прямой линии 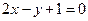 является вектор
является вектор
R 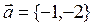
Задание {{1}} ТЗ1
Если прямая (l) проходит через точку 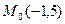 перпендикулярно прямой
перпендикулярно прямой 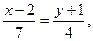 то уравнение прямой (l):
то уравнение прямой (l):
R 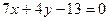
Задание {{1}} ТЗ1
Нормальным вектором прямой линии 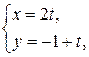 является вектор
является вектор
R 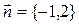
Б-базовый (10)
С-средний (7)
Т-Высокий (4)
