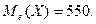Задание 1. Построить интервальный вариационный ряд распределения
Решение
1. n=100;: 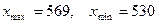 .
.
Длина частичного интервала: 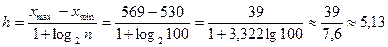
Примем h = 5. Начало первого интервала 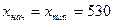
Исходные данные разбиваем на следующие равные интервалы:
(530, 535], (535, 540], (540, 545], (545, 550], (550, 555], (555, 560], (560, 565], (565, 570].
Подсчитаем 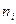 , - число студентов попавших в каждый из полученных промежутков.
, - число студентов попавших в каждый из полученных промежутков.
Таблица 1.
| Х | [530,535] | (535,540] | (540,545] | (545,550] | (550,555] | (555,560] | (560,565] | (565,570] |
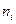 (частота) (частота) |
Задание 2. Построить гистограмму частот интервального вариационного ряда
Краткие теоретические сведения
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению 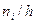 (плотность частоты).
(плотность частоты).
Для построения гистограммы на оси 0х отмечают интервалы. На оси 0у -плотность частоты. Над каждым интервалом проводят отрезки параллельные оси 0х
Площадь частичного i-го прямоугольника равна 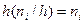 сумме частот вариант, попавших в i-й интервал. Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки n.
сумме частот вариант, попавших в i-й интервал. Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки n.
Задание 2. Построить гистограмму частот интервального вариационного ряда
Решение
Длина интервала h = 6. Найдем плотность частоты 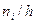 .
.
Таблица 2.
| Х | [530,535] | (535,540] | (540,545] | (545,550] | (550,555] | (555,560] | (560,565] | (565,570] |
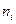 (частота) (частота) | ||||||||
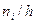 | 4/5 ≈ 0,8 | 10/5 ≈ 2 | 8/5 ≈ 1,6 | 26/5 ≈ 5,8 | 17/5 ≈ 3,4 | 23/5 ≈ 4,6 | 7/5 ≈ 1,4 | 5/5 ≈ 1 |
Задание 3. Записать эмпирическую функцию распределения
и построить ее график
Краткие теоретические сведения
Эмпирическая функция распределения 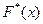 , определяет для каждого значения х относительную частоту события Х < x.
, определяет для каждого значения х относительную частоту события Х < x.
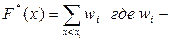 относительная частота (частость)
относительная частота (частость)
Для построения графика эмпирической функции распределения переходят к дискретному ряду распределения, для этого в качестве вариант 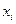 принимают середины частичных интервалов. Частоты при этом не изменяются. На оси 0х отмечают значения
принимают середины частичных интервалов. Частоты при этом не изменяются. На оси 0х отмечают значения 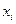 , на оси 0у – накопительные частоты.
, на оси 0у – накопительные частоты.
Задание 3. Записать эмпирическую функцию распределения
и построить ее график
Решение
Вычислим:
- середину каждого интервала 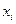 и запишем эти значения в первую строку таблицы;
и запишем эти значения в первую строку таблицы;
- относительные частоты 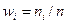 и запишем в третью строку таблицы;
и запишем в третью строку таблицы;
- накопительные частоты 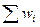 и запишем в четвертую строку таблицы.
и запишем в четвертую строку таблицы.
Таблица 3.
Значение признака 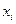 (середина интервала) (середина интервала) | 532,5 | 537,5 | 542,5 | 547,5 | 552,5 | 557,5 | 562,5 | 567,5 |
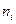 (частота) (частота) | ||||||||
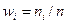 (частость) (частость) | 4/100 ≈ 0,04 | 10/100 ≈ 0,1 | 8/100 ≈ 0,08 | 26/100 ≈ 0,26 | 17/100 ≈ 0,17 | 23/100 ≈ 0,23 | 7/100 ≈ 0,07 | 5/100 ≈ 0,05 |
Накопительные относительные частоты 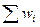 | 0,04 | 0,04+0,1= 0,14 | 0,04+0,1+0,08= 0,22 | 0,48 | 0,65 | 0,88 | 0,95 |
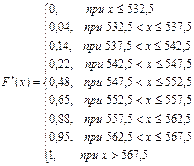
Задание 4. Рассчитать основные числовые характеристики вариационного ряда
Решение
4а) Мода – это варианта, имеющая наибольшую частоту.
По данным Таблицы 3: 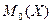 = 547,5.
= 547,5.
Медиана – это варианта, которая делит вариационный ряд на две части, равные по числу вариант. Если число интервалов четное, то медиана определяется как среднее арифметическое серединных значений интервалов, если нечетное, то медиана – это серединное значение медианного (среднего) интервала.
В нашем примере число интервалов четное
По данным Таблицы 3:(532,5+537,5+542,5+547,5+552,5+557,5+562,5+657,5)/8=550,