Предел функции в точке. Пусть функция определена в некоторой окрестности точки (т.е

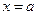Пусть функция определена в некоторой окрестности точки (т.е. в самой точке 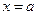функция может быть и не определена)

Определение. Число 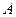называется пределом функци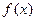и при 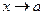, если для любого 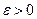существует такое число 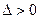, что для всех таких, что

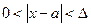
верно неравенство

.

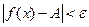То же определение может быть записано в другом виде:

Если 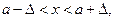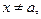то верно неравенство .

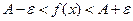Запись предела функции в точке: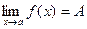

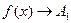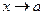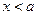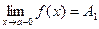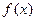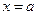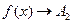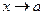Определение. Если при только при , то - называется пределом функции в точке слева, а если при только при 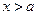, то 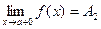называется пределом функции 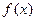в точке 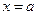справа.

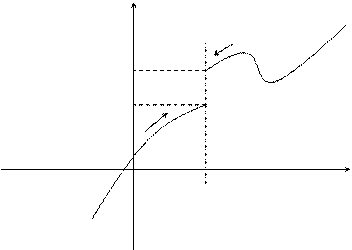
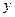
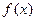
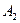
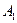
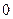
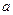
Приведенное выше определение относится к случаю, когда функция 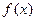не определена в самой точке 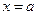, но определена в некоторой сколь угодно малой окрестности этой точки.

Пределы 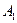и 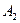называются также односторонними пределами функции 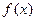в точке 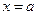. Также говорят, что 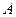– конечный предел функции .

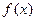Предел функции при стремлении аргумента к бесконечности

Определение. Число 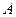называется пределом функци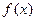и при 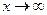, если для любого числа 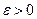существует такое число 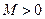, что для всех , таких что 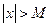выполняется неравенство

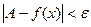
При этом предполагается, что функция 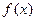определена в окрестности бесконечности.

Обозначение: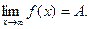

Графически это определение можно представить в виде:

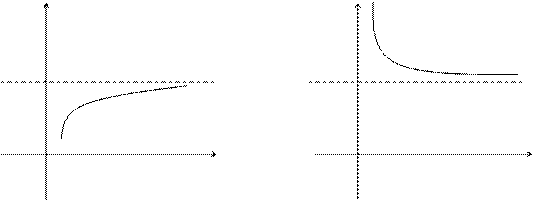y y

A A

0 0

x x

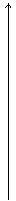y y

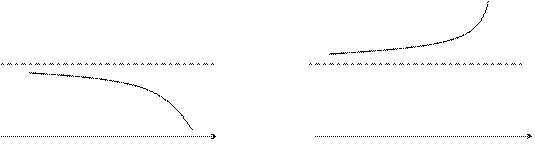A A

x x

0 0

Аналогично можно определить пределы 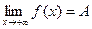для любого 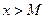и

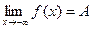для любого .

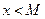Основные теоремы о пределах

Теорема 1. 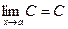, где С = const.

Следующие теоремы справедливы при предположении, что функци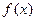и и 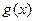имеют конечные пределы при .

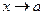Теорема 2.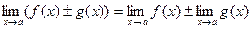

Теорема 3.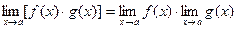

Следствие.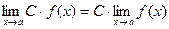

Теорема 4. 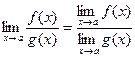при

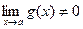
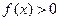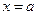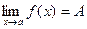Теорема 5. Если в некоторой окрестности точки и , то .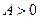

Аналогично определяется знак предела при .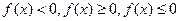

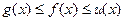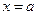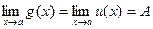Теорема 6. Если в некоторой окрестности точки и , то .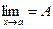

Определение. Функция 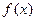называется ограниченной в некоторой окрестности точки 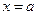, если существует такое числ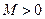о , что 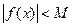для всех точек из этой окрестности.

Теорема 7. Если функция 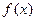) имеет конечный предел при 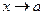, то она ограничена в некоторой окрестности точки .

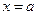Доказательство. Пусть 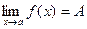, т.е. 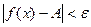, тогда

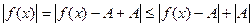или 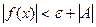, т.е. 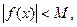где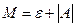

Теорема доказана.

Бесконечно малые функции и их свойства

Определение. Функция 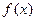называется бесконечно малой при 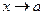, где а может быть числом или одной из величин 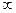, 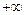или 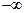, если .

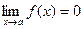Бесконечно малой функция является только при указании к какому числу стремится аргумент . При различных значениях 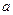функция может быть бесконечно малой или нет.

Пример. Функция 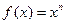является бесконечно малой при 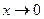и не является бесконечно малой при 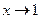, т.к. .

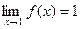Теорема. Для того, чтобы функция 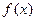при 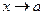имела предел, равный А, необходимо и достаточно, чтобы в некоторой окрестностии точки 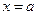выполнялось равенство

,

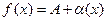где 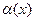– бесконечно малая при 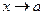фунукция ( 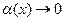при 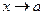).