Приложения двойных интегралов

Площадь плоской фигуры (области D) рассчитывается по формуле

S =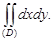

Масса тонкой плоской пластинки, являющейся областью D и с плотностью μ = μ(x; y), определяется следующим образом:

m =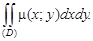

Объем цилиндрического тела, построенного на основании D, ограниченного сверху соответствующим куском поверхности z = f(x; y) и стоящего на плоскости XOY, рассчитывается следующим образом:

v =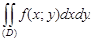

Пример 2. Расставить пределы интегрирования в двойном интеграле, если область D ограничена линиями: y = x², x = 2, y = 0 (рисунок 58).

Решение

Имеем

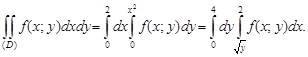
Пример 3. Изменить порядок интегрирования в интеграле

J = +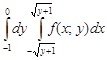

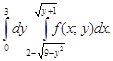
Решение

В рассматриваемом примере следует начинать с построения области интегрирования, поскольку интегралы заданы с указанием порядка интегрирования и пределов по соответствующим переменным. Напомним, что переменные пределы интегрирования внутреннего
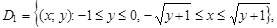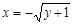интеграла являются границами изменения x при фиксированном y. Поэтому область интегрирования D₁ для первого интеграла можно задать неравенствами где и 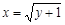представляют собой дуги параболы y = x² – 1, лежащие ниже оси Ox. Область интегрирования во втором интеграле имеет вид 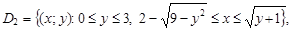где кривые 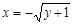и 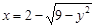представляют собой дуги параболы
y = x² – 1 и дугу окружности (x – 2)² + y² = 9, лежащие выше оси Ox.

Пусть D = D₁U D₂ (рисунок 58). Тогда каждая прямая x = const, xÎ[–1; 2], пересекает множество D по отрезку с концами y = x² – 1 и
y = 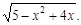Следовательно, область D можно представить в виде

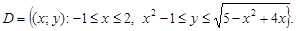
Значит,

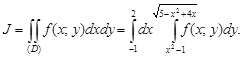
Заметим, что перемена порядка интегрирования в повторном интеграле иногда существенно упрощает его вычисление.

Пример 4.Вычислить интеграл 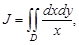где область D ограничена линиями: y = ln x, y = 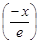+ 2и y = 0 (рисунок 59).

Решение

При каждом фиксированном значении y, y 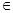[0; 1], значение x меняется от x = e^y до x = (2 – y)e. Поэтому

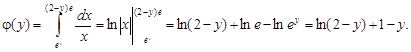
Интегрируя теперь функцию φ(y) по y в пределах от y = 0до y = 1, получим

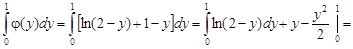
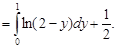
При вычислении интеграла 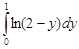используем форму интегрирования по частям. Имеем

=

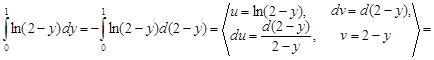
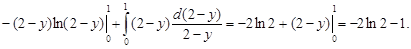
Итак,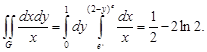

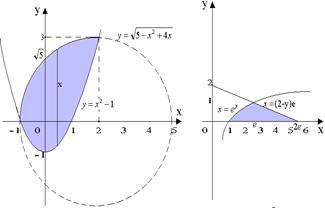
Рисунок 58 Рисунок 59

Тест 1. Связным на оси OX не является:

1) любое множество точек;

2) полуинтервал;

3) интервал;

4) вся ось OX;

5) отрезок.

Тест 2. Пусть фигура Ф – плоская область D = {(x; y): 1 ≤ x ≤ 4,
2 ≤ y ≤ 7}. Тогда диаметром Ф является число:

1) 3;

2) 5;

3) 15;

4) ;

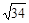5) 8.

Тест 3. Пусть фигура Ф – плоская область D = {(x; y):1 ≤ x ≤ 4,
2 ≤ y ≤7}. Тогда мерой Ф является число:

1) 3;

2) 5;

3) 15;

4) ;

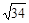5) 8.

Тест 4. Интеграл по фигуре Ф существует, если на связной ограниченной фигуре Ф функция Ф(Р):

1) определена;

2) непрерывна;

3) имеет конечное число точек разрыва;

4) имеет только точки разрыва 1-го рода;

5) имеет бесконечное число точек разрыва.

Тест 5. Пусть фигура Ф – плоская область D = {(x; y):1 ≤ x ≤ 5,
2 ≤ y ≤ 7}. Тогда 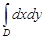равен:

1) 4;

2) 20;

3) 5;

4) ;

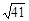5) 35.

Тест 6. Пусть фигура Ф – плоская область D = {(x; y): 1 ≤ x ≤ 5,
2 ≤ y ≤ 7}. Тогда 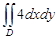равен:

1) 40;

2) 20;

3) 50;

4) 80;

5) 35.

Тест 7. Пусть Ф − фигура, ограниченная линиями y = x³, у =0,
x = 3. Тогда ее площадь равна:

1) 20,25;

2) 21;

3) 19,5;

4) 22;

5) 20,5.

Ответы на тестовые задания

Номер теста
Правильный ответ