Показатели формы распределения. Асимметрия и эксцесс

Выборочным начальным моментом k-го порядка называется величина

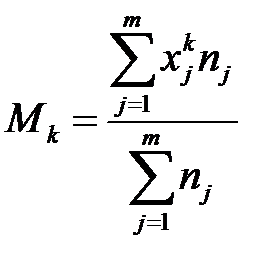. (3.24)

Нетрудно проверить, что 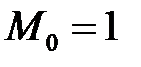, , 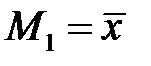где 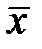— выборочная средняя.

Выборочный центральный момент k-го порядка определяется формулой

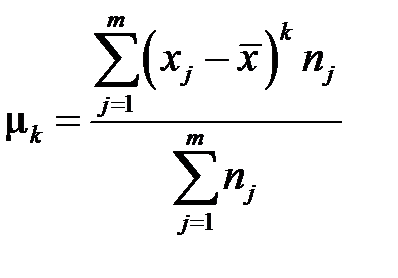. (3.25)

Из определения (3.25) следует

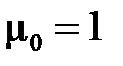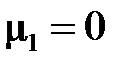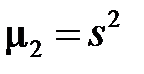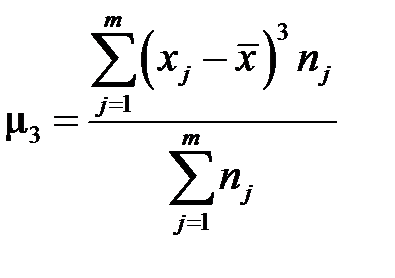, , , , (3.26)

где s² — выборочная дисперсия.

Выборочный коэффициент асимметрии определяется как отношение

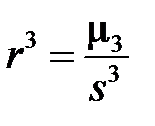(3.27)

Для симметричных распределений коэффициент асимметрии равен нулю. Знак асимметрии показывает скос распределения относительно его среднего.

Положительная асимметрия указывает на то, что справа от среднего сосредоточено больше элементов выборки, чем слева от среднего значения.

Отрицательная асимметрия указывает на отклонение распределения в сторону отрицательных значений.

В программе Excel для вычисления асимметрии предназначена функция

СКОС(Массив)

Массив — диапазон ячеек с выборочными данными, для которых вычисляется асимметрия.

Если имеется менее трех точек данных, или стандартное отклонение равно нулю, то функция СКОС возвращает значение ошибки «#ДЕЛ/0!».

Значение функции СКОС() в программе Excel вычисляется по формуле

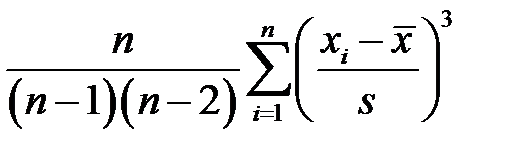, (3.28)

которая дает несмещенную состоятельную оценку асимметрии генеральной совокупности.

Выборочным эксцессом распределения называется величина

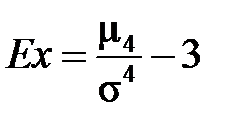(3.29)

Для нормального распределения эксцесс равен нулю.

Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс обозначает относительно остроконечное распределение. Отрицательный эксцесс обозначает относительно сглаженное распределение.

В программе Excel эксцесс вычисляет функция

ЭКСЦЕСС(Массив)

Массив — Диапазон ячеек, содержащий ряд.

Если задано менее четырех точек данных или если стандартное отклонение выборки равняется нулю, то функция ЭКСЦЕСС возвращает значение ошибки «#ДЕЛ/0!».

Значение функции ЭКСЦЕСС() в программе Excel вычисляется по следующей формуле

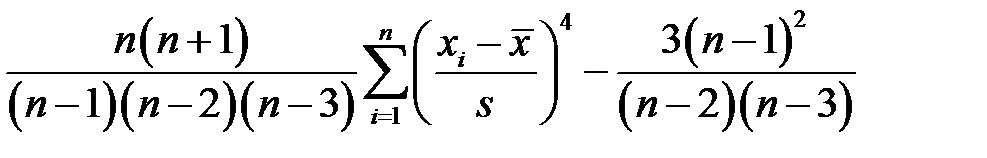. (3.30)

Формула (3.30) дает несмещенную состоятельную оценку эксцесса генеральной совокупности.

Пример 3.11. Вычислить асимметрию и эксцесс для данного вариационного ряда (табл.3.5).

Таблица 3.5

xi	2,4	2,8	3,2	3,6	4,0	4,4	4,8	5,2	5,6
ni

Решение.Введите исходные данные в диапазоне А1:В10, как показано на рис.3.11.

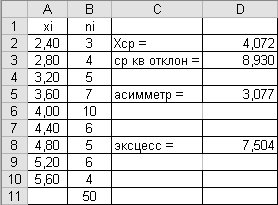
Рис.3.11

В ячейку В11 введите формулу =СУММ(B2:B10) для посчета суммы частот.

Для вычисления среднего значения в ячейку D2 введите формулу

=СУММПРОИЗВ(A2:A10;B2:B10)/СУММ(B2:B10).

Для вычисления среднеквадратического отклонения в ячейку D3 введите формулу

=КОРЕНЬ(СУММКВ(A2:A10*B2:B10-D2)/(СУММ(B2:B10)-1))

и нажмите комбинацию клавиш Ctrl + Shift + Enter, так как в параметрах функции СУММКВ(A2:A10*B2:B10-D2) используются операции с массивами.

Выражение A2:A10*B2:B10-D2 представляет операции с массивами, оно означает массив из девяти ячеек, значения который соответственно равны значениям выражений А2*В2-D2, А3*В3-D2, …, А10*В10-D2.

Для вычисления асимметрии в D5 введите формулу

=B11*СУММ(((A2:A10*B2:B10-D2)/D3)^3)/((B11-1)*(B11-2))

и нажмите комбинацию клавиш Ctrl + Shift + Enter.

Для вычисления эксцесса в D8 введите формулу

=B11*(B11+1)*СУММ(((A2:A10*B2:B10-D2)/D3)^4)/
((B11-1)*(B11-2)*(B11-3))-3*(B11-1)^2/((B11-2)*(B11-3))

и нажмите комбинацию клавиш Ctrl + Shift + Enter.

Выводы. Асимметрия вариационного ряда положительна, это значит, что большая часть вариантов находится справа от среднего.

Положительный эксцесс указывает на то, что полигон частот по сравнению с плотностью вероятностей нормального распределения имеет более остроконечную или вытянутую вверх форму.

Для контроля правильности расчетных формул можно сравнить вычисляемые значения со значениями функций СКОС и ЭКСЦЕСС. Однако эти функции не применимы к вариационному ряду, их можно применить к несгруппированной выборке.

Замените в столбце В2:В10 числа на единицы, в столбце А2:А10 введите любые числа, а в ячейках D6 и D9 введите формулы =СКОС(А2:А10) и =ЭКСЦЕСС(А2:А10).

Получим результат, показанный на рис.3.12. В ячейках D5, D6 должны быть одинаковые значения, также как и в ячейках D8, D9.

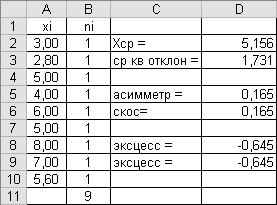
Рис.3.12

Замечание. Для сгруппированной выборки при вычислении асимметрии и эксцесса нам пришлось вводить громоздкие формулы, так как функции СКОС и ЭКСЦЕСС применимы только к несгруппированной выборке.