Закон больших чисел « в форме» теоремы Чебышева

Функция распределения случайной величины и ее свойства.

Функцией распределения случайной величины Х называется функция F(Х), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х: F(x)=P(X<x).

Функцию F(x) иногда называют интегральной функцией распределения или интегральным законом распределения.

Свойства функции распределения:

1.Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей:

0 ≤ F(x) ≤ 1.

2.Функция распределения случайной величины есть неубывающая функция на всей числовой оси.

3.На минус бесконечности функция распределения равна нулю, на плюс бесконечности равна единицы, т.е.: F(-∞)= 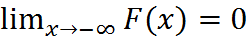, F(+∞)= .

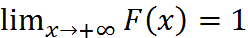4.Вероятность попадания случайной величины в интервал [х1,х2) (включая х1) равна прирощению ее функции распределения на этом интервале, т.е. Р(х₁ ≤ Х < х₂) = F(x₂ ) - F(x₁).

Неравенство Маркова и Чебышева

Неравенство Маркова

Теорема: Если случайная величина Х принимает только неотрицательные значения и имеет математическое ожидание, то для любого положительного числа А верно равенство: P(x>A) ≤ .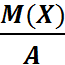

Так как события Х > А и Х ≤ А противоположные, то заменяя Р(Х >А) выражаем 1 - Р(Х ≤ А), придем к другой форме неравенства Маркова: P(X ≥ A) ≥1 - .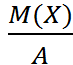

Неравенство Маркова к применимо к любым неотрицательным случайным величинам.

Неравенство Чебышева

Теорема: Для любой случайной величины, имеющей математическое ожидание и дисперсию, справедливо неравенство Чебышева:

Р (|Х – a| > ε) ≤ D(X)/ε² или Р (|Х – a| ≤ ε) ≥ 1 – DX/ε² ,где а= М(Х), ε>0.

Закон больших чисел « в форме» теоремы Чебышева.

Теорема Чебышева:Если дисперсии n независимых случайных величин Х1, Х2,…. Хn ограничены одной и той же постоянной, то при неограниченном увеличении числа n средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий а₁,а₂….,а_n, т.е .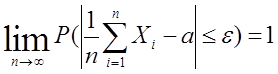

Смысл закона больших чисел заключается в том, что средние значения случайных величин стремятся к их математическому ожиданию при n → ∞ по вероятности. Отклонение средних значений от математического ожидания становится сколь угодно малым с вероятностью, близкой к единице, если n достаточно велико. Другими словами, вероятность любого отклонения средних значений от а сколь угодно мала с ростом n.

30. Теорема Бернулли.

Теорема Бернулли: Частость события в n повторных независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р, при неограниченном увеличении числа n сходиться по вероятности к вероятности р этого события в отдельном испытании: \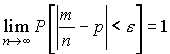

Теорема Бернулли является следствием теоремы Чебышева, ибо частость события можно представить как среднюю арифметическую n независимых альтернативных случайных величин, имеющих один и тот же закон распределения.

18.Математическое ожидание дискретной и непрерывной случайной величины и их свойства.

Математическим ожиданиемназывается сумма произведений всех ее значений на соответствующие им вероятности

Для дискретной случайной величины: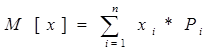

Для непрерывной случайной величины: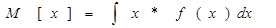

Свойства математического ожидания:

1. Математическое ожидание постоянной величины равно самой постоянной: М(С)=С

2. Постоянный множитель можно вынести за знак математического ожидания, т.е М(кХ)=кМ(Х).

3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е. M(X±Y)=M(X)±M(Y).

4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий: M(XY)=M(X)*M(Y).

5. Если все значения случайной величины увеличить (уменьшить) на постоянную С, то на эту же постоянную С увеличиться (уменьшиться) математическое ожидание этой случайной величины: M(X±C)=M(X)±C.

6. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю: M[X-M(X)]=0.