Применение производной в экономических задачах
Предельные показатели в экономике
В экономических исследованиях для обозначения производных часто пользуются специфической терминологией. Например, если f(x) есть производственная функция, выражающая зависимость выпуска какой-либо продукции от затрат фактора x, то f '(x) называют предельным продуктом; если g(x) есть функция издержек, т. е. функция g(x) выражает зависимость общих затрат от объема продукции x, то g'(x) называют предельными издержками.
Если зависимость между двумя показателями yи x задана аналитически: у = f(x) - то средняя величина представляет собой отношение y/x, а предельная - производную 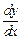 .
.
Пример 5.1.Пусть зависимость издержек производства от объема выпускаемой продукции выражается формулой 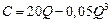 денежных единиц. Определить средние и предельные издержки при объеме продукции
денежных единиц. Определить средние и предельные издержки при объеме продукции 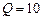 .
.
Решение.
Функция средних издержек на единицу продукции определяется по формуле
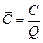 :
: 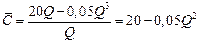 ,
,
откуда
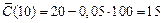 ден.ед.
ден.ед.
Предельные издержки равны производной от функции издержек, то есть
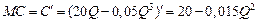 ,
,
откуда
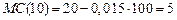 ден.ед.
ден.ед.
Таким образом при средних издержках на производство единицы продукции в 15 ден. ед. дополнительные затраты на производство единицы дополнительной продукции составляют 5 ден. ед. и не превышают средних издержек.
Понятие эластичности
Для решения экономических задач используется понятие эластичности функции, связанное с производной.
Определение.Эластичностью функции 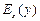 называется предел отношения относительного приращения функции y к относительному приращению переменной x при
называется предел отношения относительного приращения функции y к относительному приращению переменной x при 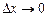
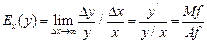 ,
,
где 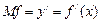 маржинальная (предельная) величина, равная производной функции по независимой переменной;
маржинальная (предельная) величина, равная производной функции по независимой переменной;
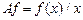 средняя величина, равная отношению функции к независимой переменной.
средняя величина, равная отношению функции к независимой переменной.
Эластичность функции y по переменной x показывает, на сколько процентов изменится функция при изменении переменной x на один процент.
Эластичность функции обладает следующими свойствами.
1. Эластичность безразмерная величина.
2. Эластичности обратных функций – обратные величины
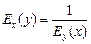
3. Эластичность произведения двух функций равна сумме эластичностей от этих функций
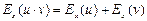
4. Эластичность дроби двух функций равна эластичности числителя минус эластичность знаменателя
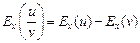
5. Эластичность суммы двух функций определяется по формуле.
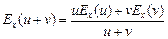
Пример 5.1. Найти эластичностьлинейной функции 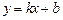 .
.
Решение.
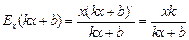
Пример 5.2. Рынок винограда в Москве может быть описан такими функциями спроса 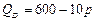 и предложения
и предложения 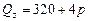 . Чему равна ценовая эластичность спроса и предложения винограда в Москве, если рынок находится в равновесии?
. Чему равна ценовая эластичность спроса и предложения винограда в Москве, если рынок находится в равновесии?
Решение.
Ценовые эластичности находим в точке равновесия. Равновесие определяется равенствами спроса и предложения товара 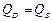 :
:
600-10P = 320+4P
Откуда получаем равновесный объем продаж Q* = 400 и равновесную цену Р* = 20
Ценовая эластичность спроса равна:
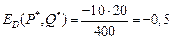
Ценовая эластичность предложения равна:
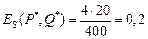
Пример 5.3.Зависимость между спросом и ценойединицыпродукции, задается соотношением 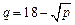 . Найти эластичность спроса и дать рекомендации о цене единицы продукции при
. Найти эластичность спроса и дать рекомендации о цене единицы продукции при 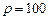 ден. ед. и
ден. ед. и 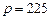 ден. ед.
ден. ед.
Решение.Найдем эластичность спроса по цене:
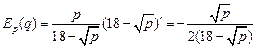 .
.
При 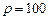 ден. ед. эластичность спроса будет равна
ден. ед. эластичность спроса будет равна
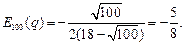
Так как 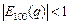 , то при цене единицы продукции в 100 ден. ед., спрос является неэластичным и можно повысить цену продукции.
, то при цене единицы продукции в 100 ден. ед., спрос является неэластичным и можно повысить цену продукции.
При 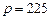 ден. ед. эластичность спроса будет равна
ден. ед. эластичность спроса будет равна
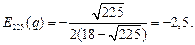
Так как 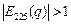 , то при цене единицы продукции в 225 ден. ед., спрос является эластичным и целесообразно рассмотреть предложение о понижении цены.
, то при цене единицы продукции в 225 ден. ед., спрос является эластичным и целесообразно рассмотреть предложение о понижении цены.
