Для студентов I курса заочной формы обучения
Государственный университет по землеустройству
Кафедра высшей математики и физики
Высшая математика
Контрольные задания для самостоятельной работы
Для студентов I и II курсов
«Заочного факультета»
Москва 2008
УДК 51
Подготовлено и рекомендовано к печати кафедрой высшей математики и физики Государственного университета по землеустройству (протокол № 10 от 28.08.2008 г).
Рецензент: Заведующий кафедрой высшей математики МЭИ доктор физико-математических наук профессор Петрушко И.М.
Авторы:
д.ф.-м.н. профессор Соловьёв И.А.,
к.ф.-м.н. доцент Хасанов А.А.,
к.ф.-м.н. доцент Червяков А.В.,
к.ф.-м.н. доцент Романов В.И.,
к.ф.-м.н. доцент Репин А.Ю.
| |
Общие указания
Предлагаемая работа содержит контрольные задания по программе первого и второго курсов высшей математики (линейная алгебра, аналитическая геометрия, математический анализ, дифференциальные уравнения, теория вероятностей и математическая статистика) для студентов «Заочного факультета» всех специальностей. В пособии приведен образец решения одного варианта.
Выполнение студентами контрольных заданий является одним из этапов изучения учебной дисциплины и подготовки к экзамену. Каждое контрольное задание выполняется в отдельной тетради и предъявляется преподавателю для защиты.
К экзамену допускаются лишь те студенты, у которых зачтены все контрольные задания, запланированные в данном семестре.
Каждый студент выполняет контрольные задания в соответствии со своим вариантом(номер варианта определяется последней цифрой номера студенческого билета или зачетной книжки).
Программа по курсу «Высшая математика»
для студентов I курса заочной формы обучения
Лекции – 18 часов.
Практические занятия –18 часов.
Контрольная работа.
Всего часов 36.
| № п/п | Тема занятия | Кол. часов |
| Лекции | ||
| 1. | Определители 2,3-го порядка и их свойства. Способы вычисления определителей. Правило Крамера. Метод Гаусса. Обратная матрица. Матричный метод решения систем квадратных линейных алгебраических уравнений. | |
| 2. | Векторы. Сложение и вычитание векторов. Умножение вектора на число. Скалярное произведение векторов и его свойства. Векторное и смешанное произведение векторов, свойства. Прямая линия на плоскости и ее уравнения. Уравнения плоскости и прямой в пространстве. | |
| 3. | Предел функции и его геометрический смысл. Вычисление пределов с помощью таблицы основных эквивалентных бесконечно малых функций. Непрерывность элементарных функций. Свойства непрерывных на отрезке функций. | |
| 4. | Производная функции в точке. Правила нахождения производной суммы, разности, произведения и отношения функций. Таблица производных основных элементарных функций. Производная сложной функции; функции, заданной параметрически; неявной функции. Первый дифференциал. | |
| 5. | Критерий монотонности дифференцируемых функций. Необходимое и достаточное условие экстремума. Критические точки первого рода. Нахождение наибольшего и наименьшего значений функции на отрезке. Определение выпуклости и вогнутости, точек перегиба. Общая схема исследования функций и построения графиков. | |
| 6. | Первообразная. Неопределенный интеграл и его свойства. Таблица основных формул интегрирования. Непосредственное интегрирование. Интегрирование по частям и подстановкой. Интегрирование рациональных дробей с помощью разложение на простейшие дроби. Интегрирование тригонометрических функций. | |
| 7. | Определение и основные свойства определенного интеграла. Производная по верхнему пределу. Формула Ньютона-Лейбница. Применение определенных интегралов к вычислению площадей плоских фигур, длин дуг кривых, объемов и площадей поверхностей вращения. Несобственные интегралы с бесконечными пределами интегрирования. Несобственные интегралы от неограниченных функций. Основные свойства. | |
| 8. | Область определения, предел и непрерывность функции нескольких переменных. Частные производные и дифференцируемость функции нескольких переменных. Экстремумы функции нескольких переменных. Производная по направлению. Градиент. | |
| 9. | Понятие числового ряда. Частичные суммы. Сходимость ряда. Необходимый признак сходимости. Достаточные признаки сходимости рядов с положительными членами: интегральный признак Коши-Маклорена; признаки сравнения («эталонные» ряды); радикальный признак Коши; признак Даламбера. Знакочередующиеся ряды: признак Лейбница. | |
| Практические занятия | ||
| 1. | Определители 2,3-го порядка и их свойства. Способы вычисления определителей. Решение СЛУ (по лекции №1). | |
| 2. | Векторы (скалярное, векторное, смешанное произведения). Элементы аналитической геометрии (по лекции №2). | |
| 3. | Вычисление пределов с помощью таблицы основных эквивалентных бесконечно малых функций. Непрерывность элементарных функций. Свойства непрерывных на отрезке функций (по лекции №3). | |
| 4. | Нахождение производных. Таблица производных основных элементарных функций. Производная сложной функции; функции, заданной параметрически; неявной функции. Первый дифференциал (по лекции №4). | |
| 5. | Нахождение наибольшего и наименьшего значений функции на отрезке. Определение выпуклости и вогнутости, точек перегиба. Общая схема исследования функций и построения графиков (по лекции №5). | |
| 6. | Таблица основных формул интегрирования. Непосредственное интегрирование. Интегрирование по частям и подстановкой. Интегрирование рациональных дробей с помощью разложение на простейшие дроби. Интегрирование тригонометрических функций (по лекции №6). | |
| 7. | Формула Ньютона-Лейбница. Применение определенных интегралов к вычислению площадей плоских фигур, длин дуг кривых, объемов и площадей поверхностей вращения. Несобственные интегралы с бесконечными пределами интегрирования (по лекции №7). | |
| 8. | Частные производные и дифференцируемость функции нескольких переменных. Экстремумы функции нескольких переменных. Производная по направлению. Градиент (по лекции №8). | |
| 9. | Понятие числового ряда. Частичные суммы. Сходимость ряда. Необходимый признак сходимости. Достаточные признаки сходимости рядов с положительными членами: интегральный признак Коши-Маклорена; признаки сравнения («эталонные» ряды); радикальный признак Коши; признак Даламбера. Знакочередующиеся ряды: признак Лейбница (по лекции №9). |
Рекомендуемая литература
1. В.С. Щипачев. Высшая математика (учебник). М.: Высшая школа 1998.
2. В.С. Щипачев. Задачник по высшей математике. М.: Высшая школа 2000.
3. Н.С. Пискунов. Дифференциальное и интегральное исчисление. Том 1 и 2. М.: Наука. 1970-1978.
4. Д.В. Беклемишев. Курс аналитической геометрии и линейной алгебры. М.: Наука. 1974.
5. Н.В. Ефимов. Краткий курс аналитической геометрии. М.: Наука. 1965-1975.
6. В.А. Кудрявцев, Б.П. Демидович. Краткий курс высшей математики. М.: Наука. 1986.
Вариант №1
Задача №1
Точки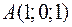 
, 
, 
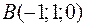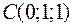и 
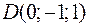являются вершинами тетраэдра.
1. Поверить, что точки 
, 
, 
, 
не лежат в одной плоскости.
2. Найти:
– объём тетраэдра;
– длину высоты тетраэдра, опущенной из вершины ;
– расстояние между скрещивающимися рёбрам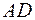и 
и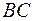 
;
– уравнение плоскости, проходящей через точки , , .
Задача №2
Найти решение системы линейных алгебраических уравнений при всех действительных значениях параметра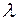 
.
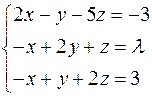Задача №3
Составить уравнение гиперболы в канонической системе координат, если в ней расстояние между вершинами –10, а расстояние между фокусами 12.
Задача №4
Вычислить пределы
а)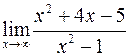 
; б) 
.
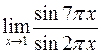Задача №5
Найти производные следующих функций
а)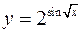 
; б)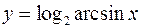 
.
Задача №6
Для следующих функций провести их полные исследования средствами дифференциального исчисления и построить их графики
а)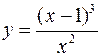 
; б)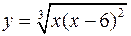 
.
Задача №7
Исследовать на экстремум следующую функцию двух переменных
.
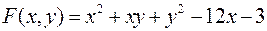Задача №8
Найти экстремумы функции
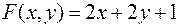
при условии
.
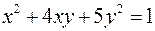Задача №9
Вычислить интегралы, пользуясь формулой Ньютона-Лейбница
а)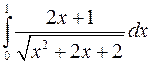 
; б) 
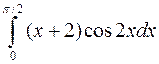; в)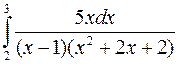 
.
Задача №10
Вычислить площадь, заключенную между линиям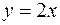и
и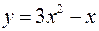 
.
Задача №11
Найти длину дуги кривой
, 
.
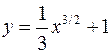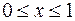Задача №12
Исследовать ряд на сходимость
.
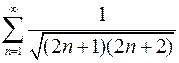Задача №13
Найти интервал сходимости степенного ряда и исследовать его на сходимость на концах этого интервала
.
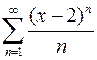Задача №14
Разложить в степенной ряд в окрестности точки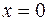 
, функцию
.
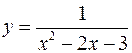Вариант №2
Задача №1
Точки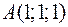 
, 
, 
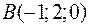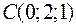и 
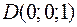являются вершинами тетраэдра.
1. Поверить, что точки , , , не лежат в одной плоскости.
2. Найти:
– объём тетраэдра;
– длину высоты тетраэдра, опущенной из вершины ;
– расстояние между скрещивающимися рёбрам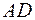и и ;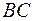
– уравнение плоскости, проходящей через точки , , .
Задача №2
Найти решение системы линейных алгебраических уравнений при всех действительных значениях параметра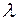
.
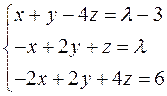Задача №3
Составить уравнение гиперболы в канонической системе координат, если эксцентриситет гиперболы равен 7/5, а расстояние от вершины до ближайшего фокуса равно 2.
Задача №4
Вычислить пределы
а)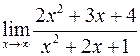 
; б) 
.
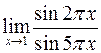Задача №5
Найти производные следующих функций
а)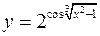 
; б)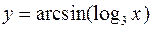 
.
Задача №6
Для следующих функций провести их полные исследования средствами дифференциального исчисления и построить их графики
а)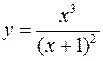 
; б)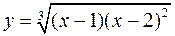 
.
Задача №7
Исследовать на экстремум следующую функцию двух переменных
.
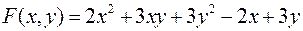Задача №8
Найти экстремумы функции
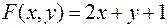
при условии
.
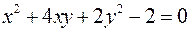Задача №9
Вычислить интегралы, пользуясь формулой Ньютона-Лейбница
а)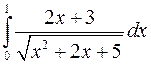 
; б) 
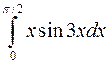; в)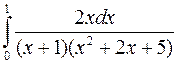 
.
Задача №10
Вычислить площадь, заключенную между линиям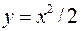и
и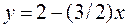 
.
Задача №11
Найти длину дуги кривой
, .
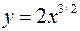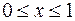Задача №12
Исследовать ряд на сходимость
.
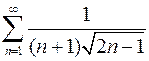Задача №13
Найти интервал сходимости степенного ряда и исследовать его на сходимость на концах этого интервала
.
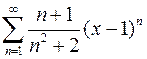Задача №14
Разложить в степенной ряд в окрестности точки 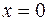, функцию
.
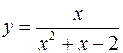Вариант №3
Задача №1
Точки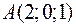 
, 
, 
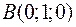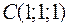и 
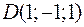являются вершинами тетраэдра.
1. Поверить, что точки , , , не лежат в одной плоскости.
2. Найти:
– объём тетраэдра;
– длину высоты тетраэдра, опущенной из вершины ;
– расстояние между скрещивающимися рёбрам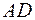и и ;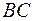
– уравнение плоскости, проходящей через точки , , .
Задача №2
Найти решение системы линейных алгебраических уравнений при всех действительных значениях параметра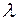
.
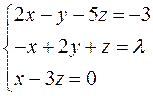Задача №3
Составить уравнение гиперболы в канонической системе координат, если уравнения директрис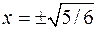 
, а точка 
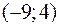принадлежит гиперболе.
Задача №4
Вычислить пределы
а)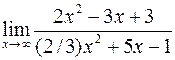 
; б) 
.
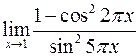Задача №5
Найти производные следующих функций
а)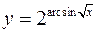 
; б)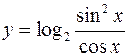 
.
Задача №6
Для следующих функций провести их полные исследования средствами дифференциального исчисления и построить их графики
а)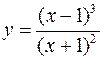 
; б)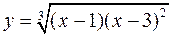 
.
Задача №7
Исследовать на экстремум следующую функцию двух переменных
.
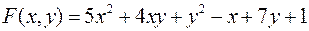Задача №8
Найти экстремумы функции
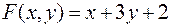
при условии
.
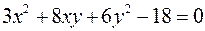Задача №9
Вычислить интегралы, пользуясь формулой Ньютона-Лейбница
а)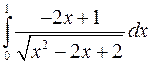 
; б) 
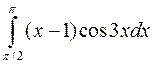; в)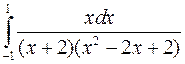 
.
Задача №10
Вычислить площадь, заключенную между линиям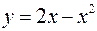и
и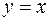 
.
Задача №11
Найти длину дуги кривой
, 
.
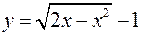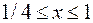Задача №12
Исследовать ряд на сходимость
.
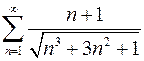Задача №13
Найти интервал сходимости степенного ряда и исследовать его на сходимость на концах этого интервала
.
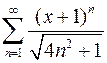Задача №14
Разложить в степенной ряд в окрестности точки 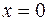, функцию
.
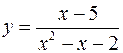Вариант №4
Задача №1
Точки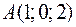 
, 
, 
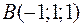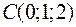и 
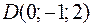являются вершинами тетраэдра.
1. Поверить, что точки , , , не лежат в одной плоскости.
2. Найти:
– объём тетраэдра;
– длину высоты тетраэдра, опущенной из вершины ;
– расстояние между скрещивающимися рёбрам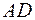и и ;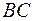
– уравнение плоскости, проходящей через точки , , .
Задача №2
Найти решение системы линейных алгебраических уравнений при всех действительных значениях параметра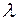
.
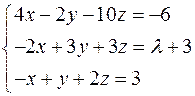Задача №3
Составить уравнение эллипса в канонической системе координат, если расстояние между вершинами на большой полуоси равно 16, а расстояние между фокусами равно 10.
Задача №4
Вычислить пределы
а)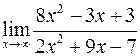 
; б) 
.
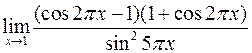Задача №5
Найти производные следующих функций
а)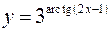 
; б)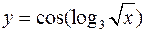 
.
Задача №6
Для следующих функций провести их полные исследования средствами дифференциального исчисления и построить их графики
а)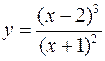 
; б)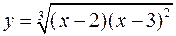 
.
Задача №7
Исследовать на экстремум следующую функцию двух переменных
.
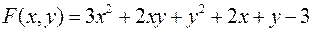Задача №8
Найти экстремумы функции
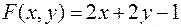
при условии
.
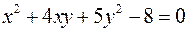Задача №9
Вычислить интегралы, пользуясь формулой Ньютона-Лейбница
а)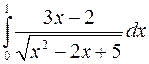 
; б) 
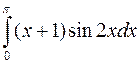; в)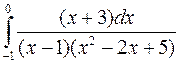 
.
Задача №10
Вычислить площадь, заключенную между линиям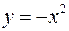и
и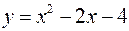 
.
Задача №11
Найти длину дуги кривой
, 
.
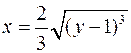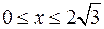Задача №12
Исследовать ряд на сходимость
.
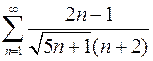Задача №13
Найти интервал сходимости степенного ряда и исследовать его на сходимость на концах этого интервала
.
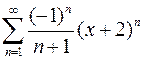Задача №14
Разложить в степенной ряд в окрестности точки 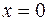, функцию
.
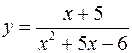Вариант №5
Задача №1
Точки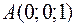 
, 
, 
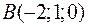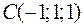и 
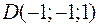являются вершинами тетраэдра.
1. Поверить, что точки , , , не лежат в одной плоскости.
2. Найти:
– объём тетраэдра;
– длину высоты тетраэдра, опущенной из вершины ;
– расстояние между скрещивающимися рёбрам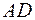и и ;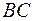
– уравнение плоскости, проходящей через точки , , .
Задача №2
Найти решение системы линейных алгебраических уравнений при всех действительных значениях параметра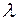
.
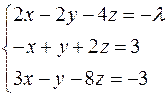Задача №3
Составить уравнение эллипса в канонической системе координат, если фокусы эллипса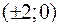 
, а уравнения директрис 
.
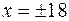Задача №4
Вычислить пределы
а)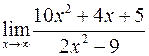 
; б) 
.
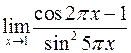Задача №5
Найти производные следующих функций
а)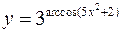 
; б)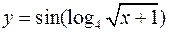 
.
Задача №6
Для следующих функций провести их полные исследования средствами дифференциального исчисления и построить их графики
а)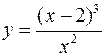 
; б)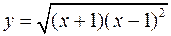 
.
Задача №7
Исследовать на экстремум следующую функцию двух переменных
.
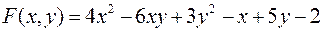Задача №8
Найти экстремумы функции
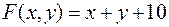
при условии
.
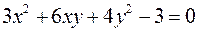Задача №9
Вычислить интегралы, пользуясь формулой Ньютона-Лейбница
а)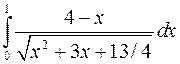 
; б) 
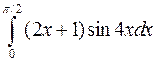; в)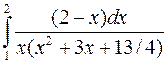 
.
Задача №10
Вычислить площадь, заключенную между линиям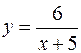и
и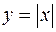 
, 
.
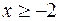Задача №11
Найти длину дуги кривой
, 
.
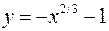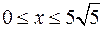Задача №12
Исследовать ряд на сходимость
.
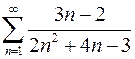Задача №13
Найти интервал сходимости степенного ряда и исследовать его на сходимость на концах этого интервала
.
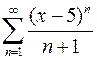Задача №14
Разложить в степенной ряд в окрестности точки 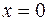, функцию
.
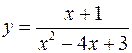Вариант №6
Задача №1
Точки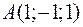 
, 
, 
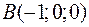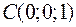и 
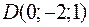являются вершинами тетраэдра.
1. Поверить, что точки , , , не лежат в одной плоскости.
2. Найти:
– объём тетраэдра;
– длину высоты тетраэдра, опущенной из вершины ;
– расстояние между скрещивающимися рёбрам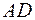и и ;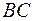
– уравнение плоскости, проходящей через точки , , .
Задача №2
Найти решение системы линейных алгебраических уравнений при всех действительных значениях параметра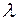
.
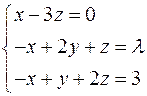Задача №3
Составить уравнение эллипса в канонической системе координат, если расстояние от директрисы до ближайшей вершины равно 4, а до вершины на оси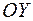 
8.
Задача №4
Вычислить пределы
а)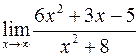 
; б)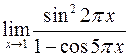 
.
Задача №5
Найти производные следующих функций
а)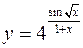 
; б)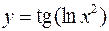 
.
Задача №6
Для следующих функций провести их полные исследования средствами дифференциального исчисления и построить их графики
а)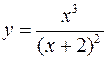 
; б)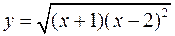 
.
Задача №7
Исследовать на экстремум следующую функцию двух переменных
.
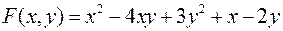Задача №8
Найти экстремумы функции
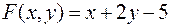
при условии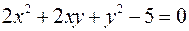 
.
Задача №9
Вычислить интегралы, пользуясь формулой Ньютона-Лейбница
а)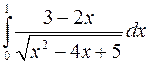 
; б) 
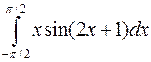; в)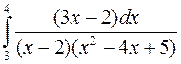 
.
Задача №10
Вычислить площадь, заключенную между линиям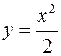и
и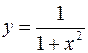 
.
Задача №11
Найти длину дуги кривой
, 
, 
.
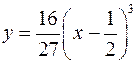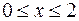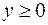Задача №12
Исследовать ряд на сходимость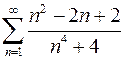 
.
Задача №13
Найти интервал сходимости степенного ряда и исследовать его на сходимость на концах этого интервала
.
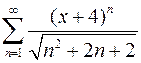Задача №14
Разложить в степенной ряд в окрестности точки 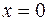, функцию
.
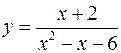Вариант №7
Задача №1
Точки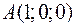 
, 
, 
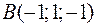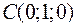и 
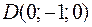являются вершинами тетраэдра.
1. Поверить, что точки , , , не лежат в одной плоскости.
2. Найти:
– объём тетраэдра;
– длину высоты тетраэдра, опущенной из вершины ;
– расстояние между скрещивающимися рёбрам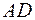и и ;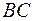
– уравнение плоскости, проходящей через точки , , .
Задача №2
Найти решение системы линейных алгебраических уравнений при всех действительных значениях параметра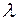
.
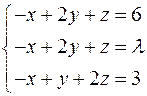Задача №3
Составить уравнение параболы в канонической системе координат, если расстояние от фокуса до директрисы равно 12.
Задача №4
Вычислить пределы
а)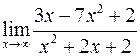 
; б) 
.
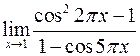Задача №5
Найти производные следующих функций
а)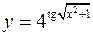 
; б)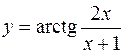 
.
Задача №6
Для следующих функций провести их полные исследования средствами дифференциального исчисления и построить их графики
а)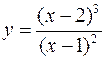 
; б)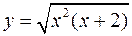 
.
Задача №7
Исследовать на экстремум следующую функцию двух переменных
.
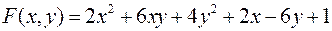Задача №8
Найти экстремумы функции
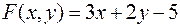
при условии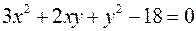 
.
Задача №9
Вычислить интегралы, пользуясь формулой Ньютона-Лейбница
а)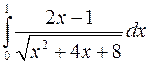 
; б) 
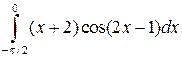; в)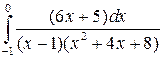 
.
Задача №10
Вычислить площадь, заключенную между линиям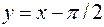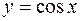и
, 
и .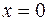
Задача №11
Найти длину дуги кривой
.
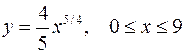Задача №12
Исследовать ряд на сходимость
.
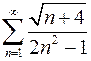Задача №13
Найти интервал сходимости степенного ряда и исследовать его на сходимость на концах этого интервала
.
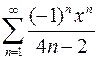Задача №14
Разложить в степенной ряд в окрестности точки 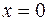, функцию
.
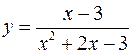Вариант №8
Задача №1
Точки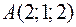 
, 
, 
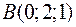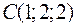и 
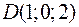являются вершинами тетраэдра.
1. Поверить, что точки , , , не лежат в одной плоскости.
2. Найти:
– объём тетраэдра;
– длину высоты тетраэдра, опущенной из вершины ;
– расстояние между скрещивающимися рёбрам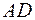и и ;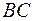
– уравнение плоскости, проходящей через точки , , .
Задача №2
Найти решение системы линейных алгебраических уравнений при всех действительных значениях параметра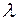
.
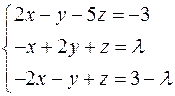Задача №3
Составить уравнение параболы в канонической системе координат, если длина хорды, проходящей через фокус под углом 450 к оси параболы, равна 18.
Задача №4
Вычислить пределы
а)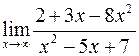 
; б) 
.
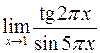Задача №5
Найти производные следующих функций
а)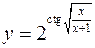 
; б)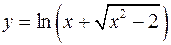 
.
Задача №6
Для следующих функций провести их полные исследования средствами дифференциального исчисления и построить их графики
а)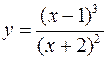 
; б)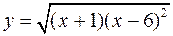 
.
Задача №7
Исследовать на экстремум следующую функцию двух переменных
.
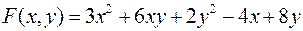Задача №8
Найти экстремумы функции
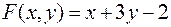
при условии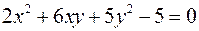 
.
Задача №9
Вычислить интегралы, пользуясь формулой Ньютона-Лейбница
а)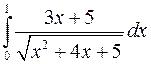 
; б) 
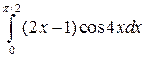; в)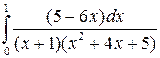 
.
Задача №10
Вычислить площадь, заключенную между линиями
, 
.
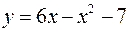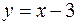Задача №11
Найти длину дуги кривой
.
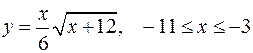Задача №12
Исследовать ряд на сходимость
.
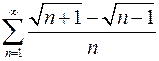Задача №13
Найти интервал сходимости степенного ряда и исследовать его на сходимость на концах этого интервала
.
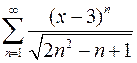Задача №14
Разложить в степенной ряд в окрестности точки 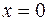, функцию
.
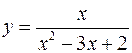Вариант №9
Задача №1
Точки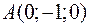 
, 
, 
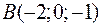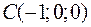и 
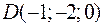являются вершинами тетраэдра.
1. Поверить, что точки , , , не лежат в одной плоскости.
2. Найти:
– объём тетраэдра;
– длину высоты тетраэдра, опущенной из вершины ;
– расстояние между скрещивающимися рёбрам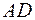и и ;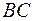
– уравнение плоскости, проходящей через точки , , .
Задача №2
Найти решение системы линейных алгебраических уравнений при всех действительных значениях параметра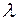
.
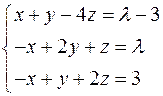Задача №3
Составить уравнение параболы в канонической системе координат, если парабола проходит через точку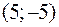 
.
Задача №4
Вычислить пределы
а)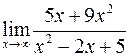 
; б) 
.
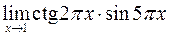Задача №5
Найти производные следующих функций
а)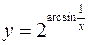 
; б)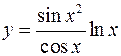 
.
Задача №6
Для следующих функций провести их полные исследования средствами дифференциального исчисления и построить их графики
а)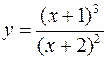 
; б)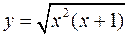 
.
Задача №7
Исследовать на экстремум следующую функцию двух переменных
.
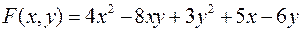Задача №8
Найти экстремумы функции
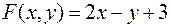
при условии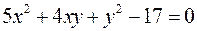 
.
Задача №9
Вычислить интегралы, пользуясь формулой Ньютона-Лейбница
а)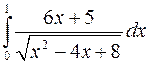 
; б) 
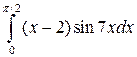; в)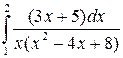 
.
Задача №10
Вычислить площадь, заключенную между линиям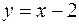и
, 
и .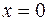
Задача №11
Найти длину дуги кривой
.
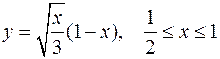Задача №12
Исследовать ряд на сходимость
.
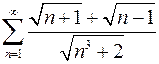Задача №13
Найти интервал сходимости степенного ряда и исследовать его на сходимость на концах этого интервала
.
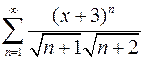Задача №14
Разложить в степенной ряд в окрестности точки 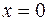, функцию
.
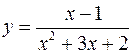Вариант №10
Задача №1
Точки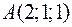 
, 
, 
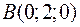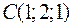и 
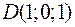являются вершинами тетраэдра.
1. Поверить, что точки , , , не лежат в одной плоскости.
2. Найти:
– объём тетраэдра;
– длину высоты тетраэдра, опущенной из вершины ;
– расстояние между скрещивающимися рёбрам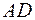и и ;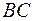
– уравнение плоскости, проходящей через точки , , .
Задача №2
Найти решение системы линейных алгебраических уравнений при всех действительных значениях параметра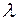
.
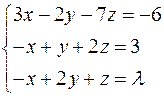Задача №3
Составить уравнение эллипса в канонической системе координат, если фокусами эллипса являются точки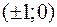 
, а точка 
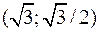принадлежит эллипсу.
Задача №4
Вычислить пределы
а)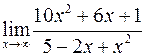 
; б) 
.
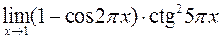Задача №5
Найти производные следующих функций
а)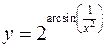 
; б)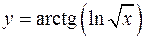 
.
Задача №6
Для следующих функций провести их полные исследования средствами дифференциального исчисления и построить их графики
а)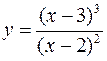 
; б)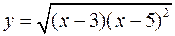 
.
Задача №7
Исследовать на экстремум следующую функцию двух переменных
.
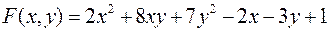Задача №8
Найти экстремумы функции
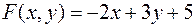
при условии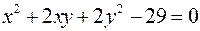 
.
Задача №9
Вычислить интегралы, пользуясь формулой Ньютона-Лейбница
а)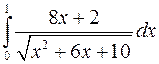 
; б) 
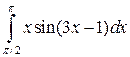; в)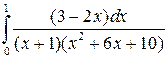 
.
Задача №10
Вычислить площадь, заключенную между линиями
, .
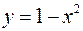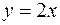Задача №11
Найти длину дуги кривой
.
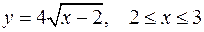Задача №12
Исследовать ряд на сходимость
.
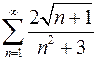Задача №13
Найти интервал сходимости степенного ряда и исследовать его на сходимость на концах этого интервала
.
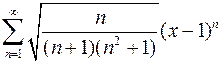Задача №14
Разложить в степенной ряд в окрестности точки 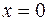, функцию
.
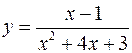Решение примерного варианта
Задача №1
Точки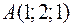 
, 
, 
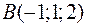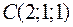и 
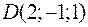являются вершинами тетраэдра.
1. Поверить, что точки , , , не лежат в одной плоскости.
2. Найти:
– объём тетраэдра;
– длину высоты тетраэдра, опущенной из вершины ;
– расстояние между скрещивающимися рёбрам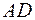и и ;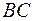
– уравнение плоскости, проходящей через точки , , .
Решение
Найдём координаты векторов:
, 
, 
.
,
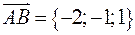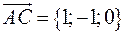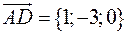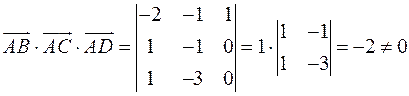следовательно, точки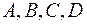 
не лежат в одной плоскости.
Объём тетраэдра:
.
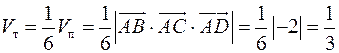Площадь основания тетраэдра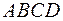 
:
.
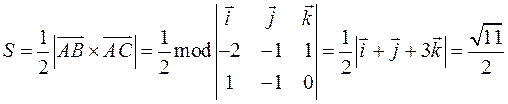Длина искомой высоты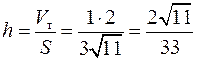 
.