A1. Элементы теории погрешностей

Задание из Таблицы №1:

а) Определить какое равенство точнее.

б) Округлить сомнительные цифра числа, оставив верные знаки: 1) в узком смысле; 2) в широком смысле. Определить предельные абсолютную и относительную погрешности результата.

в) Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры: 1) в узком смысле; 2) в широком смысле.

Таблица № 1

№	а)	б)	в)

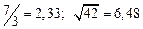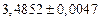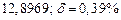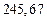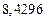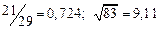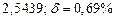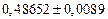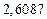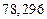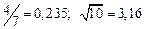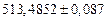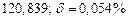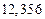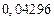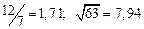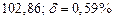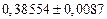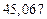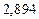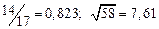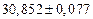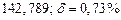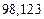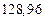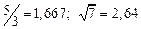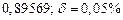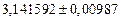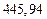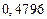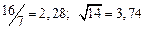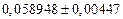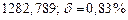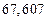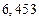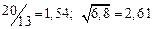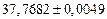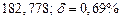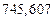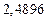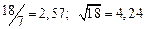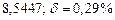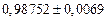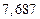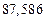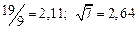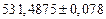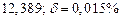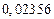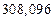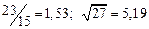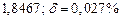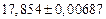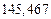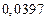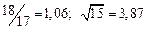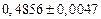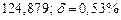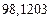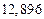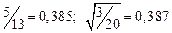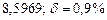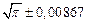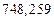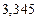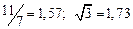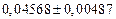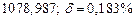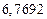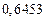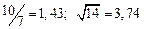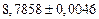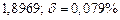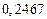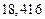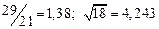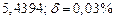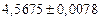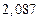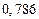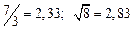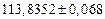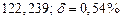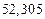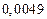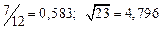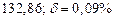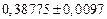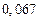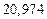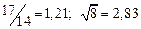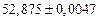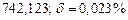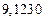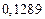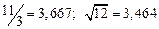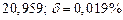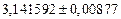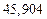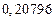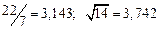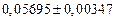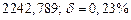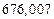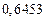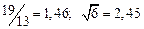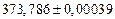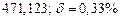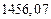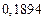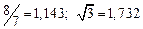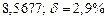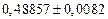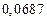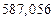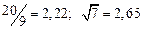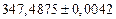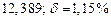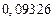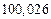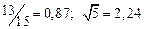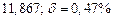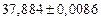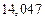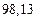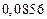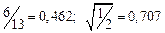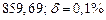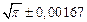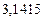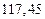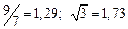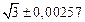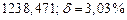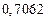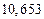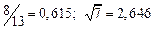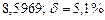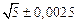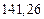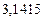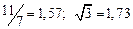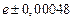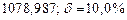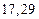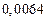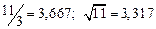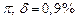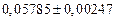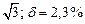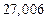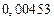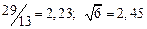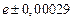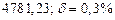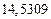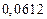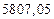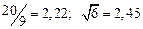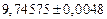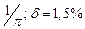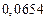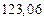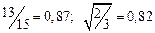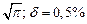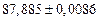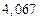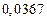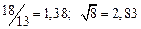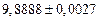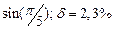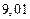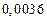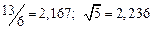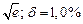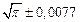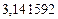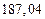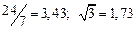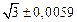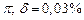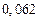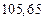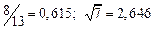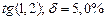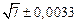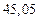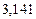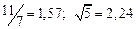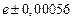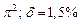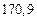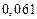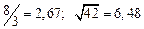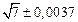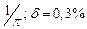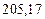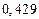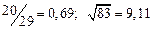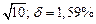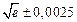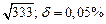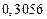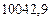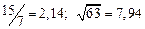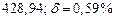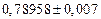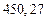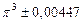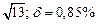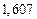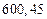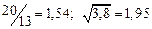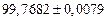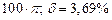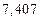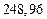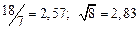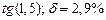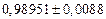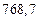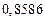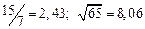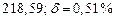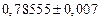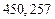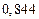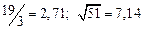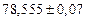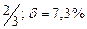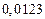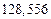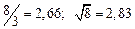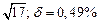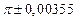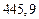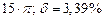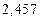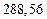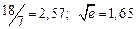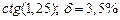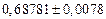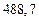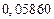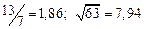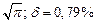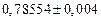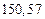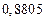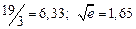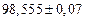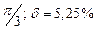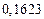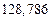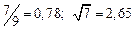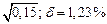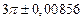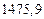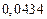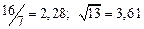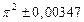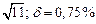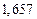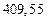Образец выполнения задания А1.

A1. a) Какое равенство точнее .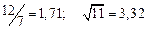

Обозначим , ; , .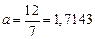

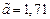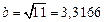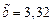Тогда , ,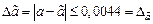

, .

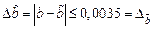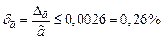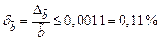Так как 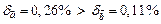, то равенство 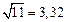определено точнее.

Ответ: Равенство 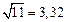определено точнее.

б)Округлить сомнительные цифра числа, оставив верные знаки: 1) в узком смысле; 2) в широком смысле. Определить предельные абсолютную и относительную погрешности результата.

1) Дано приближенное число 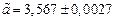, где .

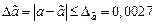Определим число верных знаков в узком смысле используя следующее выражение

.

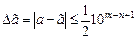Так как 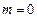, и верно неравенство 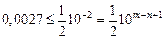, то получим 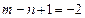, 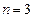. Округлим 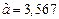до трех верных знаков и получим 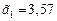с погрешностью округления 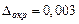. При этом погрешность полученного приближенного числа равен .

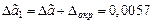Определим число верных знаков приближенного числа .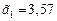

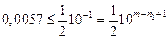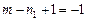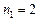, , . Округлим 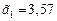до двух верных знаков и получим 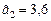с погрешностью округления 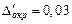. При этом погрешность полученного приближенного числа 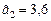равен .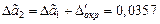

Определим число верных знаков приближенного числа .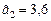

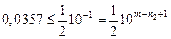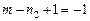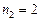, , . Так как 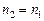, то приближенное число 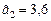имеет только верные знаки.

Определим предельную относительную погрешность приближенного числа 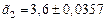. Для этого используем определение предельной погрешности: , .

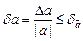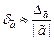Тогда получим .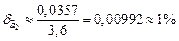

Ответ: , .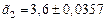

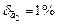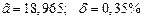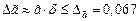2) Дано приближенное число , где . Определим число верных знаков в широком смысле используя следующее выражение .

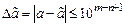Так как 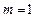, и верно неравенство 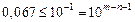, то получим 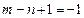, 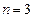. Округлим 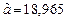до трех верных знаков и получим 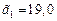с погрешностью округления 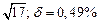. При этом погрешность полученного приближенного числа равна .

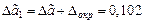Определим число верных знаков приближенного числа 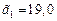. 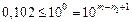, , 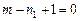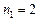. Округлим 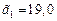до двух верных знаков и получим 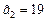с погрешностью округления 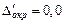. При этом погрешность полученного приближенного числ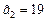а равна .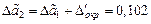

Определим число верных знаков приближенного числа .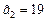

Из условия 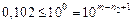, получим 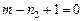, 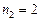. Так как 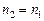, то приближенное число 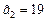имеет только верные знаки.

Определим предельную относительную погрешность приближенного числа 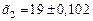. Для этого используем определение предельной погрешности: , .

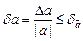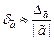Тогда получим .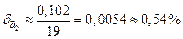

Ответ: , .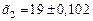

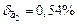в) Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры: 1) в узком смысле; 2) в широком смысле.

1) Дано приближенное число .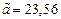

Так как это число имеет только верные цифры в узком смысле, то 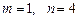. Определим предельную абсолютную погрешность числа из выражения 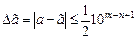. Тогда .

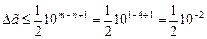Следовательно, для предельной абсолютной погрешности имеем 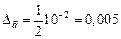. Для определения предельной относительной погрешности числа можно использовать выражение .

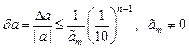Так как 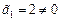, то .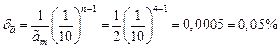

Ответ: .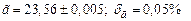

2) Дано приближенное число .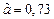

Так как это число имеет только верные цифры в широком смысле, то 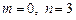. Определим предельную абсолютную погрешность числа из выражения 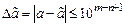. Тогда .

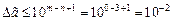Следовательно, для предельной абсолютной погрешности имеем 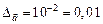. Для определения предельной относительной погрешности числа можно использовать выражение .

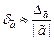Тогда, получим .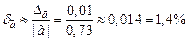

Ответ: .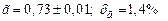

A2. Элементы теории погрешностей.

а) Вычислить и определить предельные абсолютную и относительную погрешности результата.

б) Вычислить и определить предельные абсолютную и относительную погрешности результата.

в) Вычислить и определить предельные абсолютную и относительную погрешности результата пользуясь общей формулой погрешности: 1) в узком смысле; 2) в широком смысле.

Задание из Таблицы 2 определяется по следующей схеме:

Если 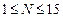, то номер задания равен номеру варианта ( 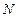), а исходные данные из Кол.1;

Если 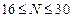, то номер задания равен ( 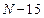) , а исходные данные из Кол.2;

Если 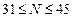, то номер задания равен ( 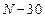) , а исходные данные из Кол.3;

Если 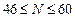, то номер задания равен ( 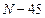) , а исходные данные из Кол.4.

Таблица 2