Элементы теории погрешностей
Определение 1.1.Приближенным значением некоторой величины a называется число аp, которое незначительно отличатся от точного значения этой величины.
Пусть а — точное значение некоторой величины, а аp — ее приближенное значение.
Определение 1.1. Абсолютной погрешностью D приближенного значения называется модуль разности между точным и приближенным значениями этой величины:
D = |a – ap| (1.2)
Пример 1.1. Если a = 20,25 и ap = 20, то абсолютная погрешность равна D = 0,25.
Определение 1.2.Относительной погрешностью приближенной величины аp называется отношение абсолютной погрешности приближенной величины к её точному значению:
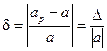(1.3)
Это равенство можно записать в другой форме
D = |a|δ. (1.4)
Пример 1.2. Пусть a = 20,25 и ap = 20. Тогда относительная погрешность равна δ = 0,25/20 = 0,125.
На практике, как правило, точное значение величины неизвестно. Поэтому, вместо теоретических понятий абсолютной и относительной погрешностей используют практические понятия предельной абсолютной погрешности и предельной относительной погрешности [7].
Определение 1.3.Под предельной абсолютной погрешностью приближенного числа понимается всякое число Da, не меньшее абсолютной погрешности этого числа
D = |a – ap| ≤ Da (1.5)
Неравенство (1.5) позволяет для точного значения величины получить оценку
ap – Da ≤ a ≤ ap + Da (1.6)
Часто неравенства (1.6) записывают в другой форме
a = ap ± Da = ap(1 ± δa) (1.7)
На практике в качестве предельной абсолютной погрешности выбирают наименьшее из чисел Da, удовлетворяющих неравенству (1.5), однако это не всегда возможно.
Пример 1.3.Оценить предельную абсолютную погрешность приближенного значения ap = 2,72 числа e, если известно, что e = 2,718281828….
Решение. Очевидно, что |ap – e| < 0,01. Следовательно, Da = 0,01. Также справедливо неравенство |ap – e| = |2,720 – 2,71828…| < 0,002. Получаем другое значение предельной абсолютной погрешности Da = 0,002. Ясно, что следует выбрать наименьшее из найденных значений предельной погрешности, т.к. это позволит сузить диапазон (1.5), в котором находится точное значение изучаемой величины. С другой стороны, погрешность Da = 0,01 показывает, что приближенное число 2,72 содержит верные цифры. Значение Da = 0,002 не дает возможности утверждать, что число 2,720 содержит четыре верные цифры.
Определение 1.4.Предельной относительной погрешностью δa данного приближенного числа называется любое число, не меньшее относительной погрешности этого числа:
δ ≤ δa (1.8)
Так как справедливо неравенство
,
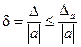то можно считать, что предельные абсолютная и относительная погрешности связаны формулой
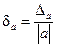или Da = |a|δa. (1.9)
Пример 1.4.Пусть длина бруска измерена сантиметровой линейкой и получено приближенное значение ap = 251 см. Найти предельную относительную погрешность δa.
Решение. Так как сантиметровая линейка не содержит делений меньше сантиметра, то предельная абсолютная погрешность равна Da = 1 см, а точное значение a длины бруска находится в диапазоне 250 см ≤ a ≤ 252 см. Хотя точное значение a неизвестно, можно для относительной погрешности записать неравенство
.
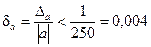То есть, можно считать, что δa = 0,004.
Если абсолютная погрешность Da значительно меньше точного значения |a|, то относительную погрешность определяют приближенно как отношение абсолютной погрешности к приближенному значению:
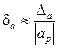, Da ≈ |ap|δa (1.10)
Часто в формуле (1.10) вместо знака «≈» используют знак точного равенства «=».
Относительную погрешность иногда задают в процентах.
Пример 1.5.Определить предельную относительную и абсолютную погрешности значения x = 125 ± 5%.
Решение. Здесь δa = 5% = 0,05 и Da = 0,05∙125 = 6,25.
В этом примере мы воспользовались формулой (1.10).
Значащие цифры.
Определение 1.5. Значащими цифрами в записи приближенного числа называются
─ все ненулевые цифры;
─ нули, содержащиеся между ненулевыми цифрами;
─ нули, являющиеся представителями сохраненных десятичных разрядов при округлении.
В следующих примерах значащие цифры подчеркнуты:
Пример 1.6. 2,305; 0,0357; 0,001123; 0,035299879 ≈ 0,035300.
При округлении числа 0,035299879 до шести знаков после запятой получается число 0,035300, в котором последние два нуля являются значащими. Если отбросить эти нули, то полученное число 0,0353 не является равнозначным с числом 0,035300 приближенным значением числа 0,035299879, так как погрешности указанных приближенных чисел отличаются!
Дадим определение понятию верная значащая цифра [7].
Определение 1.6.Первые n значащих цифр в записи приближенного числа называются верными в узком смысле, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего n-ой значащей цифре, считая слева направо.
Наряду с определением 1.6 иногда используется другое определение [7]:
Определение 1.7.Первые n значащих цифр в записи приближенного числа называются верными в широком смысле, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего n-ой значащей цифре.
Пример 1.7.Определить верные цифры приближенного значения
ap = 2,721 числа e, если известно, что e = 2,718281828….
Решение. Очевидно, что |ap – e| = |2,721 – 2,71828…| < 0,003 < 0,005.
Следовательно, верными являются только три первые цифры, последнюю цифру можно отбросить, ap = 2,72.
Пример 1.8.Пусть x = 1,10253 ± 0,00009. Верными являются первые четыре значащие цифры, а цифры 5 и 3 не удовлетворяют определению. В широком смысле верными являются первые пять цифр.
Пример 1.9. При записи следующих физических констант указаны три верные значащие цифры:
а) гравитационная постоянная γ = 6,67∙10–11 Н∙м2/кг2;
б) скорость света в вакууме C = 3,00∙108 м/c;
в) постоянная Планка h = 6,63∙10–34 Дж∙c.
Замечание.Термин «верные значащие цифры» нельзя понимать буквально. Например, современное опытное значение скорости света в вакууме составляет C = 2,997925∙108 м/c. Очевидно, что ни одна значащая цифра в примере 9, б) не совпадает с соответствующей точной цифрой, но абсолютная погрешность меньше половины разряда, соответствующего последней значащей цифре в записи 3,00∙108:
|3,00∙108 – 2,997925∙108| < 0,003∙108 < 0,01∙108/2 = 0,005∙108.
Правило округления чисел [7].Чтобы округлить число до n значащих цифр, отбрасывают все цифры его, стоящие справа от n-й значащей цифры, или, если это нужно для сохранения разрядов, заменяют их нулями. При этом
1) если первая отброшенная цифра меньше 5, то оставшиеся десятичные знаки сохраняют без изменения;
2) если первая отброшенная цифра больше 5, то к последней оставшейся цифре прибавляют единицу;
3) если первая отброшенная цифра равна 5, и среди остальных отброшенных цифр есть ненулевые, то к последней оставшейся цифре прибавляют единицу;
3а) если же первая из отброшенных цифр равна 5, и все отброшенные цифры являются нулями, то последняя оставшаяся цифра оставляется неизменной, если она четная, и увеличивается на единицу, если она нечетная (правило четной цифры).
Это правило гарантирует, что сохраненные значащие цифры числа являются верными в узком смысле, то есть погрешность округления не превосходит половины разряда, соответствующего последней оставленной значащей цифре. Правило четной цифры должно обеспечить компенсацию знаков ошибок.
Пример 1.10.Приведем примеры округления до 4-х значащих цифр:
а) 3,1415926 ≈ 3,142; Dp = |3,142 – 3,1415926| < 0,00041 < 0,0005;
б) 1 256 410 ≈ 1 256 000; Dp = |1 256 000 – 1 256 410| < 500;
в) 2,997925∙108 ≈ 2,998∙108; Dp = |2,998∙108 – 2,997925∙108| =
= 0,000075∙108 < 0,0005∙108.
Следующая теорема выявляет связь относительной погрешности числа с числом верных десятичных знаков [7].
Теорема 1.1. Если положительное приближенное число имеет n верных значащих цифр, то его относительная погрешность δ не превосходит величины 101–n, деленной на первую значащую цифру αm:
δ ≤ 101–n/ αm. (1.11)
Формула (1.11) позволяет вычислить предельную относительную погрешность
δa = 101–n/ αm (1.12)
Пример 1.11. Найти относительную и абсолютную погрешности приближенных чисел а) 3,142 и б) 2,997925∙108.
Решение. а) Здесь n = 4, αm = 3; Используем формулу (1.12) для оценки относительной погрешности: δa = 101–n/ αm = 0,001/3 ≈ 0,00033. Для определения абсолютной погрешности применим формулу (1.10):
Da ≈ |ap|δa = 3,142∙0,00033 ≈ 0,001.
б) Аналогично предыдущему пункту вычислим: n = 7, αm = 2,
δa = 101–n/ αm = 0,000001/2 = 0,0000005;
Da ≈ |ap|δa = 2,997925∙108∙0,0000005 ≈ 150.