Элементы теории погрешностей.
Конспект лекций
Численные методы.
Элементы теории погрешностей.
Понятие погрешности.
Различают два вида погрешностей - абсолютную и относительную. Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения. Относительная погрешность - это отношение абсолютной погрешности к истинному значению числа.
Абсолютной погрешностью приближенного числа а назовем величину ∆а, про которую известно, что 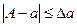 .
.
Таким образом, точное число заключено в границах 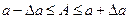 или сокращенно
или сокращенно 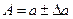 .
.
Пример. Приближенные числа а1=2,87; а2=300; а3=3*102 получены округлением, точные значения чисел неизвестны. Что можно сказать об абсолютной погрешности данных приближенных чисел?
Решение. Пользуясь правилами округления чисел, можно сказать, что абсолютные погрешности приближенных чисел не превосходят половины единицы последнего разряда, т.е.
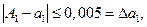
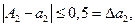
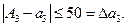
Для приближенного числа, полученного в результате округления, абсолютная погрешность ∆a принимается равной половине единицы последнего разряда числа.
Пример. Значение а=0,734 могло быть получено округлением чисел 0.73441, 0.73353 и др. При этом ∆a≤0,0005, и полагаем ∆a=0,0005.
При вычислениях на ЭВМ округления, как правило, не производятся, а цифры, выходящие за разрядную сетку машины, отбрасываются. В этом случае максимально возможная погрешность результата выполнения операции в два раза больше по сравнению со случаем округления.
Абсолютная погрешность связана с размерностью и не полностью характеризует результат. Например, известно, что абсолютная погрешность равна 3 см. Ясно, что имеем совершенно различный по точности результат, если речь идет о длине карандаша или о расстоянии между Землей и Сатурном. Поэтому вводят понятие относительной погрешности.
Относительной погрешностью δа приближенного числа а называется отношение абсолютной погрешности ∆а к абсолютной величине приближенного числа а: 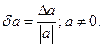
Для приближенного числа, полученного в результате округления, абсолютная погрешность ∆a принимается равной половине единицы последнего разряда числа. Например, значение а=0.734 могло быть получено округлением чисел 0.73441, 0.73353 и др. При этом ∆a≤0.0005, и полагаем ∆a=0.0005.
Приведем примеры оценки абсолютной погрешности при некоторых значениях приближенной величины а.
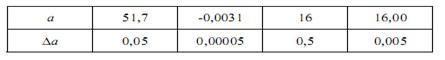
При вычислениях на ЭВМ округления, как правило, не производятся, а цифры, выходящие за разрядную сетку машины, отбрасываются. В этом случае максимально возможная погрешность результата выполнения операции в два раза больше по сравнению со случаем округления.
Например: относительная погрешность δ(-2.3) = 0.05/2.3 ≈ 0.022 (2.2%). Заметим, что погрешность округляется всегда в сторону увеличения. В данном случае δ(-2.3) ≈ 0.03.
Определение. Значащими цифрами в десятичной записи числа называются все цифры, начиная с первой ненулевой слева.
Определение. Значащая цифра называется верной в узком смысле, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.
Определение. Значащая цифра называется верной в широком смысле, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.
Сформулируем правила округления:
1. если отбрасываемые при округлении цифры составляют число, большее половины единицы последнего оставляемого разряда, то последняя оставляемая цифра увеличивается на единицу;
2. если отбрасываемые при округлении цифры составляют число, меньшее половины единицы последнего оставляемого разряда, то оставляемые цифры остаются без изменения;
3. при округлении, когда отбрасываемые цифры составляют число, равное половине единицы последнего оставляемого разряда, то последняя оставляемая цифра увеличивается на единицу, если она нечетная, и остается без изменения, если она четная (правило четной цифры).
Ловушки вычислений
Полученная оценка относительной погрешности содержит в знаменателе выражение |1 – x|. Ясно, что при х ≈ 1 можем получить очень большую погрешность. В связи с этим рассмотрим подробнее случай вычитания близких чисел.
Запишем выражение для относительной погрешности разности двух чисел в виде
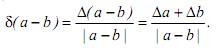
При а ≈ b эта погрешность может быть сколь угодно большой.
Пример 2. Пусть а = 2520, b = 2518. В этом случае имеем абсолютные погрешности исходных данных ∆а = ∆b = 0.5 и относительные погрешности δa ≈ δb = 0.5/2518 ≈ 0.0002 (0.02%). Относительная погрешность разности равна
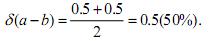
Следовательно, при малых погрешностях в исходных данных мы получили весьма неточный результат. Нетрудно подсчитать, что даже при случайных изменениях а и b на единицу, в последних разрядах их разность может принимать значения 0, 1, 2, 3, 4. Поэтому, при организации вычислительных алгоритмов следует избегать вычитания близких чисел; при возможности алгоритм нужно видоизменить во избежание потери точности на некотором этапе вычислений.
Из рассмотренных правил следует, что при сложении или вычитании приближенных чисел желательно, чтобы эти числа обладали одинаковыми абсолютными погрешностями, т. е. одинаковым числом разрядов после десятичной точки. Например, 38.723+4.9=43.6; 425.4-0.047=425.4. Учет отброшенных разрядов не повысит точность результатов. При умножении и делении приближенных чисел количество значащих цифр выравнивается по наименьшему из них.
Рассмотрим также некоторые другие случаи, когда можно избежать потери точности правильной организацией вычислений.
Пусть требуется найти сумму пяти четырехразрядных чисел: S = 0.2764 + 0.3944 + 1.475 + 26.46 + 1364. Складывая все эти числа, а затем, округляя полученный результат до четырех значащих цифр, получаем S = 1393. Однако при вычислении на машине округление происходит после каждого сложения. Предполагая условно сетку четырехразрядной, проследим вычисление на машине суммы чисел от наименьшего к наибольшему, т. е. в порядке их записи: 0.2764 + 0.3944 = 0.6708, 0.6708 + 1.475 = 2.156, 2.156 + 26.46 = 28.62, 28.62 + 1364 = 393; получили S1 = 1393, т. е. верный результат. Изменим теперь порядок вычислений и начнем складывать числа последовательно от последнего к первому: 1364 + 26.46 = 1390, 1390 + 1.475 = 1391, 1391 + 0.3944 = 1391, 1391 + 0.2764 = 1391; здесь окончательный результат S1 = 1391, он менее точный.
Анализ процесса вычислений показывает, что потеря точности здесь происходит из-за того, что прибавления к большому числу малых чисел не происходит, поскольку они выходят за рамки разрядной сетки (а + b = а при а » b). Этих малых чисел может быть очень много, но на результат они все равно не повлияют, поскольку прибавляются по одному. Здесь необходимо придерживаться правила, в соответствии с которым сложение чисел нужно проводить по мере их возрастания. В машинной арифметике из-за погрешности округления существен порядок выполнения операций, и известные из алгебры законы коммутативности (и дистрибутивности) здесь не всегда выполняются.
Максимальная относительная погрешность при округлении есть δmax=0.5α1-k, где α — основание системы счисления, k— количество разрядов мантиссы числа. При простом отбрасывании лишних разрядов эта погрешность увеличивается вдвое.
При решении задачи на ЭВМ нужно использовать подобного рода «маленькие хитрости» для улучшения алгоритма и снижения погрешностей результатов. Например, при вычислении на ЭВМ значения (а +х)2 величина х может оказаться такой, что результатом сложения а + х получится а (при х « а); в этом случае может помочь замена (а + х)2 = а2 + 2ах + х2.
Рассмотрим еще один важный пример — использование рядов для вычисления значений функций. Запишем, например, разложение функции sin(х) по степеням аргумента:
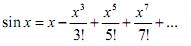
По признаку Лейбница остаток сходящегося знакочередующегося ряда, т. е. погрешность суммы конечного числа членов, не превышает значения первого из отброшенных членов (по абсолютной величине).
Вычислим значение функции sin(х) при х = 0.5236 (30°). Члены ряда, меньшие 10-4, не будем учитывать. Вычисления проведем с четырьмя верными знаками. Получим 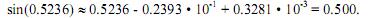
Это отличный результат в рамках принятой точности. Зная из курса высшей математики, что это разложение синуса справедливо при любом значении аргумента (-∞ < х < ∞), используем его для вычисления функции при х =6.807 (390°). Опуская вычисления, получаем sin(6.807) ≈ 0.5493. Относительная погрешность составляет здесь около 10% (вместо ожидаемого значения 0.01% по признаку Лейбница). Это объясняется погрешностями округлений и способом суммирования ряда (слева направо, без учета величины членов).
Нe всегда помогает и повышенная точность вычислений. В частности, для данного ряда при х = 25.66 (1470° = 4 ⋅ 360°+30°) даже при учете членов ряда до 10 и вычислениях с восемью значащими цифрами в результате аналогичных вычислений (суммирование слева направо) получается результат, не имеющий смысла: sin(25.66) ≈ 24.
В программах, использующих степенные ряды для вычисления значений функций, могут быть приняты различные меры по предотвращению подобной потери точности. Так, для тригонометрических функций можно использовать формулы приведения, благодаря чему аргумент будет находиться на отрезке [0, 1].
При вычислении экспоненты аргумент х можно разбить на сумму целой и дробной частей (ex = en+a = enea) и использовать разложение в ряд только для еa, а еn вычислять умножением.
Таким образом, при организации вычислений можно своевременно распознать подобные «подводные камни», когда возможна потеря точности, и попытаться затем исправить положение.
Алгоритмы уточнения корня
1. Алгоритм уточнения корня методом половинного деления
Сущность метода.Пусть каким-либо методом найден отрезок изоляции корня [а; b] уравнения F(х) = 0, где F(х) - непрерывна на участке [a; b], (а)*F(b) < 0. В дальнейшем требуется сузить этот отрезок так, чтобы его длина стала не больше заранее заданной точности вычисления корня e, то есть чтобы |b - a| £ e.
Этот процесс сужения интервала, содержащего изолированный корень уравнения F(х) = 0, называется уточнением корня.
В этом алгоритме отрезок изоляции корня [а; b] точкой с = 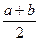 делят пополам и вычисляют значение F(c). Если F(c) = 0, то с - значение искомого корня уравнения, и задача решена. Если F(c) ¹ 0, то искомый корень уравнения содержится в одном из двух отрезков [a; c] или [c; b], на концах которого функция F
делят пополам и вычисляют значение F(c). Если F(c) = 0, то с - значение искомого корня уравнения, и задача решена. Если F(c) ¹ 0, то искомый корень уравнения содержится в одном из двух отрезков [a; c] или [c; b], на концах которого функция F  принимает значения разных знаков. Обозначим этот отрезок через [a1, b1], его длина b1-a1 =
принимает значения разных знаков. Обозначим этот отрезок через [a1, b1], его длина b1-a1 = 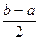 . С отрезком [a1, b1] поступают точно так, как и с отрезком [a, b]. Этот процесс последовательного деления отрезка пополам продолжают до тех пор, пока не произойдет одно из двух:
. С отрезком [a1, b1] поступают точно так, как и с отрезком [a, b]. Этот процесс последовательного деления отрезка пополам продолжают до тех пор, пока не произойдет одно из двух:
§ либо найдется такая точка cn = 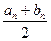 , в которой F(cn) = 0 (что маловероятно!), и задача решена;
, в которой F(cn) = 0 (что маловероятно!), и задача решена;
§ либо такой точки не найдется, но при некотором n придем к отрезку [an, bn] длины bn - an = 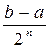 £ e, содержащему в себе искомый корень.
£ e, содержащему в себе искомый корень.
Тогда числа an и bn являются приближенными значениями искомого корня с требуемой точностью e соответственно с недостатком и с избытком. Однако лучше за приближенное значение искомого корня взять число сn = 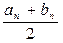 , погрешность которого не превышает
, погрешность которого не превышает 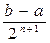 .
.
2. Алгоритм уточнения корня методом хорд
Сущность метода. Пусть отрезок изоляции [a; b] корня х уравнения F(х) = 0 найден, причем для определенности пусть F(a) < 0, F(b) > 0 и F'(х) > 0. График функции y = F(х) проходит через точки A(a; F(a)) и B(b; F(b)) (рис. 1). Составим уравнение хорды АВ как прямой, проходящей через точки А и В:
y = kx + l;
F(a) = ka + l;
F(b) = kb + l;
k = 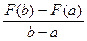 ; l = F(a) - a
; l = F(a) - a 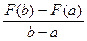
y= 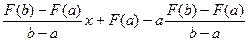
y - F(a) = 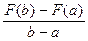 (x - a).
(x - a). 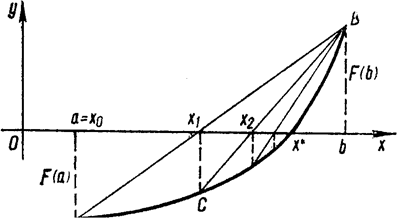
Рисунок 1 – Графическое представление метода хорд
далее находим абсциссу x1 точки пересечения хорды АВ с осью Ох, уравнение которой y = 0: 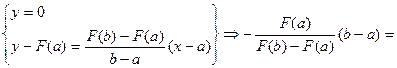
= x1 - a Þ x1 = a - 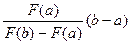 .
.
Число x1 примем за первое приближение корня х*. Далее, применяя этот же прием к отрезку изоляции [x1; b], на концах которого функция F(x) принимает противоположные знаки, получим второе приближение корня x2:
x2 = x1 - 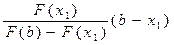
Этот процесс можно продолжать неограниченно. Описанный процесс называется методом хорд. В результате получим последовательность вложенных отрезков[a; b] É [x1; b] É [x2; b] É ... É [xn; b] É ...с неподвижным концом b. Последовательные приближения xn (n = 1, 2, ...) к точному значению корня х* вычисляются по формуле
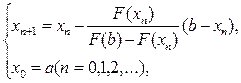 (3)
(3)
называемой формулой метода хорд, и образуют монотонно возрастающую последовательность a = x0 < x1 < x2 < ... < xn < xn+1 < ... < b, ограниченную сверху числом b. По теореме Вейерштрасса эта последовательность имеет предел
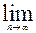 xn =
xn = 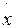 *.
*.
Поскольку F(х) непрерывна на [а; b], то 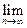 F(xn) = F(
F(xn) = F( 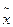 *).
*).
Переходя теперь к пределу в равенстве (3), получаем
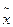 * =
* = 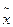 * -
* - 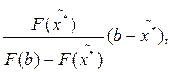
откуда, так как b - 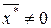 , следует, что F(
, следует, что F( 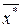 ) = 0. Но в связи с тем, что уравнение F(x) = 0 на отрезке [а; b]имеет единственный корень х*, то х* = х*.
) = 0. Но в связи с тем, что уравнение F(x) = 0 на отрезке [а; b]имеет единственный корень х*, то х* = х*.
Поскольку полученная последовательность (х„) сходится к корню уравнения х*, то любой ее член можно рассматривать в качестве приближенного значения корня. Практически последовательные приближения вычисляют до тех пор, пока не получат приближенное значение корня с требуемой точностью.
3.Алгоритм уточнения корня методом касательных
Сущность метода.Пусть [а; b] — отрезок изоляции корня х* уравнения F(х) = 0. И пусть для определенности F(a)<0, F(b)>0, F‘(x)>0 и F”(x)>0, xÎ[а; b], то есть производные сохраняют постоянный знак (рис.2). Идея метода касательных, предложенного Ньютоном, сводится к замене небольшой дуги
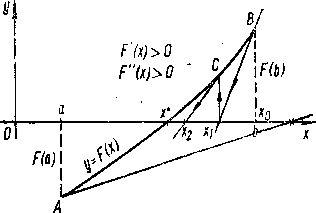
Рисунок 2 – Графическое представление метода касательных
кривой у = F(х) касательной к кривой, проведенной в некоторой точке интервала [а; b]. Выберем, например, x0 = b, так как F(x0) ´ F¢¢(x0)>0, и в точке В(x0, F(х0)) проведем касательную к кривой у = F(х). Ее уравнение:
y - F(x0) = F¢(x0)(x - x0).'
Найдем теперь точку пересечения x1 касательной с осью Ох(у = 0):
0 - F(x0) = F¢(x0)(x1 - x0) Þ x1 = x0 - 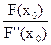
Эту точку x1 принимаем за первое приближение искомого корня х*. Через точку С(x1; F(x1)) снова проведем касательную y - F(x1) = F‘(x1)(x - x1), абсциссу точки пересечения которой с осью Ох примем за второе приближение х2 корня х*. Имеем:
0 - F(x1) = F‘(x1)(x2 - x1) Þ x2 = x1 - 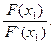
Продолжая этот процесс далее, получим рекуррентную формулу,
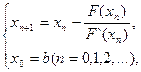 (8)
(8)
называемую формулой метода касательных.
Заметим, что если в рассматриваемом случае (F’(x) > О, F”(x) > О, F(b) > 0, F(а) < 0) касательную провести в точке А, то есть положить x0 = а, то точка пересечения ее с осью абсцисс может оказаться вне отрезка изоляции корня [a; b]. Это значит, что метод касательных неприменим, если в качестве начальной точки x0 выбрать такую, в которой F(x0) ´ F”(x0) < 0.
Как и в методе хорд, можно доказать (предлагаем читателю сделать это самостоятельно), что полученная числовая последовательность
x0>x1>x2>...>xn>xn+1>...>a
сходится к корню уравнения х*.
Для оценки погрешности приближения xn можно воспользоваться, как и в методе хорд, формулой
½x* - xn½ £ ½xn - xn-1½ £ e.
Анализируя возможные расположения кривой у = F(х)на отрезке изоляции, где последовательные приближения по методу касательных обозначены 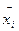 (i = 0,1,2...), получаем правило для использования метода касательных: в качестве начального приближения x0 выбирается тот конец отрезка изоляции (x0 = а или x0 = b), в котором выполняется условие
(i = 0,1,2...), получаем правило для использования метода касательных: в качестве начального приближения x0 выбирается тот конец отрезка изоляции (x0 = а или x0 = b), в котором выполняется условие
F(x0) F¢¢(x0) > 0 (9)
Пример 9. Методом касательных найти корень уравнения
F(x) = 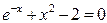
на отрезке [1; 2] с точностью до e = 10-5.
Находим: F‘(x) = - 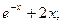 F¢¢(x) =
F¢¢(x) = 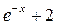 .
.
Применив формулу (8), имеем:
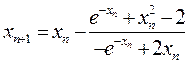 (n = 0, 1, 2, ...).
(n = 0, 1, 2, ...).
Выберем начальное приближение x0, используя условие (9). Имеем:
F(1) = 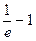 < 0;
< 0;
F(2) = 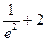 > 0;
> 0;
F¢¢(1) = 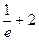 > 0;
> 0;
F¢(2) = 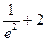 >0.
>0.
Поскольку F(2)´F”(2) > 0, то касательную следует проводить в правом конце отрезка, то есть x0 = b = 2.
Последовательные приближения вычисляем на ЭВМ, заполняя табл. 7.
| Xn | F(xn)= 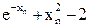 | F‘(xn)= 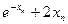 | 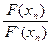 | ½xn – xn-1½ | |
| (2) - (5) | 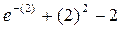 | e-(2)+2×(2) | 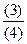 | ||
| 2,0 | 2,135335 | 3,864665 | 0,552528 | ||
| 1,5 | 0,473130 | 2,776870 | 0,170382 | 0,5 | |
| 1.38 | 0,033377 | 2,395523 | 0,013933 | 0,17 | |
| 1,316 | 0,000062 | 2,363794 | 0,000026 | 0,014 | |
| 1,8159738 | 0.0000005 | 2,3637346 | 0,0000002 | 0,0000262 | |
| 1,3159736 | - 0,0000005 | 2,3637342 | -0,0000002 | 0,0000002 |
Если в качестве приближенного значения корня взять число 1,3159736, то невязка F(1,3159737) = - 0,0000003.
4. Комбинированный метод хорд и касательных
Сущность метода.Рассмотренные выше метод хорд и метод касательных (каждый в отдельности) позволяют приблизиться к корню уравнения лишь с одной стороны: либо слева (приближение с недостатком), либо справа (приближение с избытком), причем всегда, если формула хорд дает приближение корня с недостатком, то формула касательных — с избытком, и наоборот. Одновременное применение этих двух методов на каждом шаге дает возможность искомый корень уравнения взять в вилку и не выпускать его из нее до достижения заданной точности.
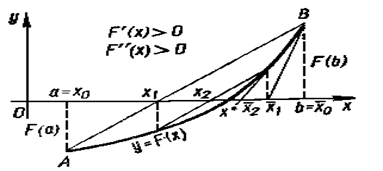
Рисунок 3 – Иллюстрация метода хорд и касательных
Пусть (рис.3) условие F( 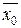 )×F«(
)×F«( 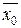 ) > 0 выполняется в правом конце отрезка изоляции корня (
) > 0 выполняется в правом конце отрезка изоляции корня ( 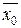 = b). Тогда последовательные значения с недостатком х0 = а, x1, x2, ... , xn, xn+1, ... вычисляют методом хорд:
= b). Тогда последовательные значения с недостатком х0 = а, x1, x2, ... , xn, xn+1, ... вычисляют методом хорд:
xn+1 = xn - 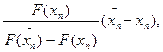 x0 = a(n = 0, 1, 2, ...), (10)
x0 = a(n = 0, 1, 2, ...), (10)
а последовательные значения корня с избытком
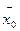 = b,
= b, 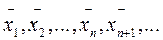
вычисляют методом касательных (8):
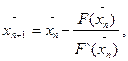
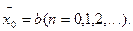 (11)
(11)
По формулам (10) и (11) вычисляют приближенные значения корня соответственно с недостатком и с избытком, причем для всех n xn < х* < хn.
Если при некотором n выполняется неравенство 0 < ½ 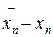 ½ £ e то в качестве приближенного значения искомого корня с точностью e принимают среднее арифметическое значение полученных двусторонних приближений, то есть x =
½ £ e то в качестве приближенного значения искомого корня с точностью e принимают среднее арифметическое значение полученных двусторонних приближений, то есть x = 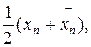 так как тогда½x - x*½ < ½
так как тогда½x - x*½ < ½ 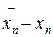 ½ £ e.
½ £ e.
Если условие 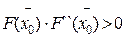 выполняется в левом конце отрезка изоляции корня, тогда
выполняется в левом конце отрезка изоляции корня, тогда
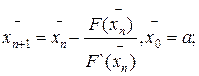 (12)
(12)
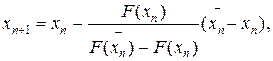 x0 = b (n = 0,1,2,...), (13)
x0 = b (n = 0,1,2,...), (13)
то есть формула касательных дает приближение корня с недостатком, а формула хорд—с избытком.
Обращаем внимание читателя на следующее обстоятельство. Если в формулах (3) и (7) метода хорд (его иногда называют стационарным методом хорд) один конец отрезка изоляции корня в процессе вычислений все время оставался неподвижным, то в формулах (10) и (13) комбинированного метода хорд и касательных оба конца отрезка изоляции корня являются подвижными. На каждом шаге вычислений в качестве неподвижного конца формулы метода хорд используется приближенное значение искомого корня, вычисленное по формуле метода касательных (рис. 22).
Пример. Комбинированным методом хорд и касательных найти корень уравнения
F(х) = Зх - cos х - 1 = 0 на отрезке [0; 1] с точностью e = 10-4
Так как F(х) непрерывная функция, a F’(x) = 3 +sin х > 0, х Î R; F(0) = -2 < 0 и F(1) = 2 - cos1 > 0, то на отрезке [0; 1] имеется единственный корень уравнения. Вторая производная
F”(x) = cos х> 0, х Î [0; 1].
Условие F(х)•F”(x) > 0 выполняется в точке х = 1, то есть F(1)•F(2) > 0. Следовательно, уточнение корня выполняем по формулам:
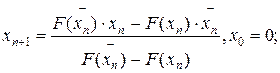
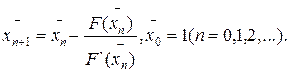
Вычисления на ЭВМ оформляем в табл. 8, в которую введены промежуточные графы, облегчающие вычисление значений функции и производной.
Таблица 8 Расчетная таблица метода хорд и касательных
| Xn | 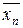 | 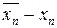 | F(xn) | 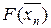 | 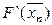 | 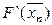 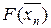 | 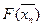 xn - F(xn) xn - F(xn) 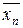 | |
| n | (9):(8) | (3) –(6): (7) | (3) - (2) | 3*(2) - соs(2) – 1 | 3*(3) – cos(3) - 1 | 3 + sin(3) | (6) - (5) | (6)*(2)- (5)*(3) |
| -2 | 1,459697 | 3,841471 | 3,459697 | |||||
| 0,5780853 | 0,6200162 | 0,0419309 | -0,1032551 | 0,0461796 | 3,581048 | 0,1494401 | 0,0907188 | |
| 0,6070577 | 0,6071207 | 0,0000630 | xср=0.5 ( 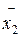 - x2) = 0,607089 - x2) = 0,607089 |
О точности полученных приближений (x2, 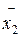 , xcp) можно судить по невязке:
, xcp) можно судить по невязке:
F(x2) = F(0,6070577) = - 0,0001569,
F( 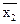 ) = F(0,6071207) = 0,0000681,
) = F(0,6071207) = 0,0000681,
F(xcp) = F(0,6071) = 0,000006.
5. Метод последовательных приближений (итераций)
Сущность метода. Для нахождения действительных корней уравнения F(x) = 0, где F(x) - непрерывная функция на [a; b], его заменяют равносильным уравнением
х = j(х) (14)
Это можно сделать всегда, притом не одним способом. Например, уравнение
х3 - 9х + 3 = 0
можно представить так: 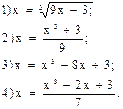
Пусть известен отрезок изоляции корня [a; b], тогда за начальное приближение искомого корня уравнения (14) берут: 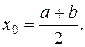 Подставляя значение х0 в правую часть уравнения (14), получают первое приближение х1 = j(х0). В качестве второго приближения берут х2 = j(х1). Продолжая этот процесс дальше, получают числовую последовательность (хn), определенную с помощью рекуррентной формулы:
Подставляя значение х0 в правую часть уравнения (14), получают первое приближение х1 = j(х0). В качестве второго приближения берут х2 = j(х1). Продолжая этот процесс дальше, получают числовую последовательность (хn), определенную с помощью рекуррентной формулы:
xn+1 = j(xn), (n = 0, 1, 2, ...) (15)
Полученная последовательность х0, х1, ..., xn, xn+1,... называется итерационной последовательностью, способ построения ее называется методом последовательных приближений или методом итераций численного решения уравнения.
При пользовании методом итераций необходимо выяснить основной вопрос: сходится ли полученная последовательность (хn) к решению х* уравнения (14) при возрастании n? Если последовательность (хn) сходится, то есть существует предел х* = 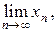 то, переходя к пределу в равенстве (15) и, предполагая, что функция j(х) непрерывна, получаем:
то, переходя к пределу в равенстве (15) и, предполагая, что функция j(х) непрерывна, получаем:
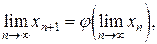 или x* = j(x*). (16)
или x* = j(x*). (16)
Следовательно, в этом случае х = х* является корнем уравнения х = j(х), а значит, и уравнения F(x) = 0.
Если же последовательность (хn) окажется расходящейся, то есть не существует конечного предела построенной последовательности приближений (хn), то это означает, что процесс итераций построен неудачно, и его надо заменить другим.
Следовательно, метод последовательных приближений применим при выполнении условия:
½j‘(x)½ £ M1 < 1 (18)
для всех х, принадлежащих отрезку изоляции корня уравнения (14), В этом случае процесс итераций сходится, и тем быстрее, чем меньше М1; если же ½j‘(x)½ > 1, то итерационный процесс расходится. Для конкретной оценки величины m1, определяющей скорость сходимости, проще всего пользоваться формулой: М1 = max½j‘(x)½, где max берется по отрезкуизоляции корня [а: b].
Основной этап.
Шаг 1. Положить lymj равным оптимальному решению задачи минимизации f(yj+lym*dj) при условии, что lym принадлежит E1. Положить y[j+1]= yj+lymj*dj. Если j < n, то заменить j на j+1 и вернуться к шагу 1. Если j=n, то перейти к шагу 2.
Шаг 2. Положить x[k+1] = y[n+1]. Если || x[k+1] - xk || < eps, то остановиться. В противном случае положить y1= x[k+1], j=1, заменить k на k+1 и перейти к шагу 1.
Метод Хука и Дживса.
Метод Хука и Дживса осуществляет два типа поиска - исследующий поиск и поиск по образцу. Первые две итерации процедуры показаны на рисунке.
При заданном начальном векторе x1 исследующий поиск по координатным направлениям приводит в точку x2 . Последующий поиск по образцу в направлении x1- x2 приводит в точку y. Затем исследующий поиск, начинающийся из точки y, дает точку x3. Следующий этап поиска по образцу вдоль направления x3- x2 дает y*. Затем процесс повторяется.
Метод наискорейшего спуска
Метод наискорейшего спуска является одной из наиболее фундаментальных процедур минимизации дифференцируемой функции нескольких переменных. Вектор d называется направлением спуска для функции f в точке x, если существует такое d > 0, что f(x+lym*d)<f(x) для всех lym принадлежащих интервалу (0, d). В частности, если
| f(x+ld)-f(x) | ||
| lim | -------------------< 0, | при lym->0+ |
| lym |
то d - направление спуска. В методе наискорейшего спуска осуществляется движение вдоль направления d, для которого ||d|| = 1 и которое минимизирует приведенный выше предел. Если f дифференцируема в точке x и grad(f(x))!=0, то -grad(f(x))/||grad(f(x))|| является направлением наискорейшего спуска. В связи с этим метод наискорейшего спуска иногда называют градиентным методом.
Численное интегрирование
Постановка задачи
Вычисление скалярных аддитивных величин обычно сводится к суммированию бесконечно большого числа беcконечно малых слагаемых такого вида:
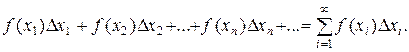
Например, если значение функции f(xi) считать проекцией силы на ось Ох, а малую величину Dхi - “элементарным” перемещением некоторой массы под действием этой силы, то произведение f(xi) Dхi = DАi даст “элементарную” работу DАi силы f на малом перемещении Dхi. Работа силы f на всем перемещении массы по свойству аддитивности будет равна сумме “элементарных” работ
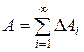
Но так как физически не представляется возможным просуммировать бесконечно много слагаемых DАi, то, ограничиваясь n слагаемыми, можно получить приближенное значение данной величины:
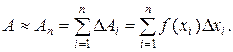
Точное значение таких величин выражается с помощью предельного перехода, в результате которого получают интеграл:
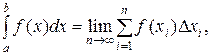
где [a; b] - отрезок, на котором задана функция f.
Определение понятия интеграла и его геометрическую интерпретацию.
Пусть на конечном отрезке [a; b] задано непрерывную функцию f (рисунок 3), причем f(x) > 0, x Î [a; b] и a < b.
1.Разобьем отрезок [a; b] произвольным образом на n частичных отрезков точками:
a = x0 < x1 < x2 <...< xi < xi+1 < ... < xn = b.
2.Обозначим длину каждого частичного отрезка через
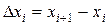 (i = 0, 1, 2,...,n - 1).
(i = 0, 1, 2,...,n - 1).
3.Выберем произвольно в каждом частичном отрезке точку
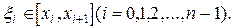
4.Составим произведения значений функции f в точке 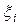 на длину i-го отрезка, т.е.
на длину i-го отрезка, т.е.
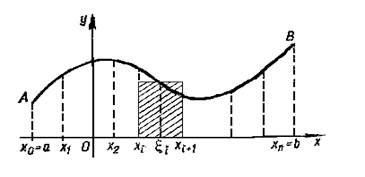
Рисунок 4
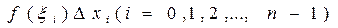
Геометрически это произведение дает площадь “элементарного” i-го прямоугольника, заштрихованного на рисунке 4.
Просуммируем полученные произведения
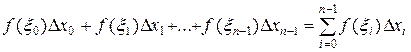 : (1)
: (1)
Полученную таким образом сумму (1) называют интегральной суммой. Геометрически эта сумма дает площадь всех n ’’элементарных’’ прямоугольников, то есть площадь ступенчатой фигуры. Отметим, что интегральных сумм (1) можно построить бесконечно много в силу того, что при их построении допускается два произвола: разбиение отрезка [a, b] на части точками хi и выбор точек 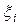 (i = 0, 1, ... ,n-1) на каждом из частичных отрезков
(i = 0, 1, ... ,n-1) на каждом из частичных отрезков 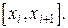
6. Выполним предельный переход при условии, что 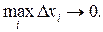
Если при 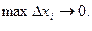 интегральная сумма (1) имеет конечный предел, то этот предел называется интегралом функции f от а до b и обозначается
интегральная сумма (1) имеет конечный предел, то этот предел называется интегралом функции f от а до b и обозначается 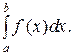
Следовательно, 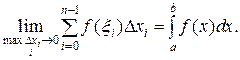 (2)
(2)
Таким образом, интегралом функции f на отрезке интегрировании от а до b называется предел интегральных сумм при условии, что максимальная длина частичных отрезков стремится к нулю, следовательно, число их неограниченно возрастает, то есть 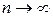 .
.
В силу непрерывности функции f площадь ступенчатой фигуры (рис.33) при большом n “почти совпадает” с площадью криволинейной трапеции аAвb, а при 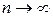 интеграл (2) и дает точное значение площади S криволинейной трапеции с основанием [a; b], ограниченной сверху графиком функции f:
интеграл (2) и дает точное значение площади S криволинейной трапеции с основанием [a; b], ограниченной сверху графиком функции f:
S = 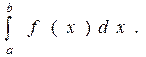
Можно доказать, что если функции f непрерывна на отрезке [a; b], то предел (2) существует.
Формула (2) непригодна для точного вычисления интеграла, так как операция вычисления предела интегральной суммы практически не всегда легко выполнима.
Для вычисления точного значения интеграла (2) используют понятие первообразной функции. Пусть подынтегральная функция f непрерывна на отрезке [a; b] и известна ее первообразная F, то есть такая функция, что
F‘(x) = f(x), x 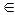 [a; b].
[a; b].
Тогда интеграл (2) может быть вычислен по формуле Ньютона-Лейбница
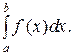 = F(b) - F(a), (3)
= F(b) - F(a), (3)
как приращение первообразной функции F на отрезке [a; b].
Кроме того, можно доказать, что если существует интеграл (3), то одной из первообразных функций на [a;b] для подынтегральной функции является интеграл с переменным верхним пределом 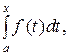 так как
так как
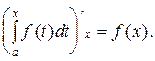
Таким образом, если мы умеем найти первообразную функцию, то можем вычислить также и интеграл.
Однако очень часто нахождение первообразной функции затруднительно, громоздко или вообще невыполнимо в элементарных функциях. Тогда задача вычисления точного значения интеграла по формуле Ньютона-Лейбница (3) оказывается неразрешимой. Класс функций f, для которых первообразная F выражается через элементарные функции, весьма узок, а , значит, и формула (3) не всегда пригодна для практики. Например, не выражается в элементарных функциях первообразная для функции
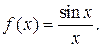
В таких случаях действие интегрирования порождает новый класс неэлементарных функций. Так, для приведенной выше функции получаем (по определению) неэлементарную функцию
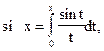 (4)
(4)
которую называют интегральным синусом. Значение этой функции, например, при х = 1 равно 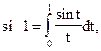 то есть значением функции является интеграл, не выражающийся в элементарных функциях, а не число в явном виде, что было бы практически значительно удобнее. Кроме того, на практике часто подынтегральная функция f задается графически или таблично, тогда само понятие первообразной теряет смысл и формула Ньютона - Лейбница, несмотря на ее большое теоретическое и практическое значение, опять “не работает”.
то есть значением функции является интеграл, не выражающийся в элементарных функциях, а не число в явном виде, что было бы практически значительно удобнее. Кроме того, на практике часто подынтегральная функция f задается графически или таблично, тогда само понятие первообразной теряет смысл и формула Ньютона - Лейбница, несмотря на ее большое теоретическое и практическое значение, опять “не работает”.
Таким образом, приходится иметь дело с интегралами, которые не выражаются в элементарных функциях. В этих случаях незаменимое значение приобретает приближенное интегрирование. Для приближенного интегрирования функций разработано много численных методов. Сущность этих методов состоит в том, что значение интеграла вычисляется приближенно по формулам вида
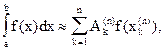 (5)
(5)
в которых используется ряд значений по
