Умножение вектора на число

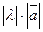Произведением вектора на число l называется вектор, длина которого равна , а направление

1) совпадает с направлением , если число l>0;

2) противоположно ему, если l<0.

Свойства операции умножения вектора на число

1⁰ .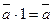

2⁰ Умножение ассоциативно относительно умножения чисел:

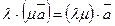
3⁰ Умножение дистрибутивно относительно сложения чисел:

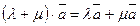
4⁰ Умножение дистрибутивно относительно сложения векторов:

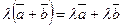
Линейная зависимость системы векторов

Пусть дан набор векторов 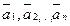и набор действительных чисел .

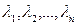Вектор называют линейной комбинацией системы векторов с данными коэффициентами, если имеет место равенство

,

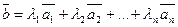Говорят также, что в этом случае линейно выражается через данные векторы 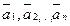, т.е. получается из них с помощью линейных действий.

Пример 1 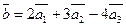есть линейная комбинация векторов 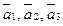с коэффициентами 2, 3, -4.

Если вектор представлен как линейная комбинация каких-то векторов, то говорят, что он разложен по этим векторам.

Конечная система векторов 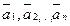называется линейно зависимой системой, если существует не нулевой набор чисел 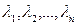, такой что линейная комбинация данной системы векторов с данными коэффициентами есть нулевой вектор.

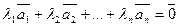
В противном случае, т.е. когда соотношение 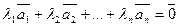выполняется только при 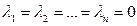, эти векторы называются линейно независимыми.

Теорема (о линейной зависимости системы векторов).

Если система векторов содержит вектор, являющийся линейной комбинацией некоторых векторов данной системы, то вся система линейно зависима.

Следствие Если система содержит нулевой вектор, то она линейно зависима.

Теорема Любые два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Теорема Пусть даны два неколлинеарных вектора. Тогда любой вектор, компланарный с ними может быть представлен в виде линейной комбинации данных векторов.

Следствие Три вектора линейно зависимы тогда и только тогда, когда они компланарны.

Теорема Пусть даны три некомпланарных вектора. Тогда любой (четвертый) вектор пространства может быть представлен в виде линейной комбинации этих векторов.

Следствие Любые четыре вектора пространства линейно зависимы.

Базис. Координаты вектора

Базисом векторного пространства называют упорядоченную систему векторов 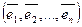, обладающую следующими свойствами:

1 данная система линейно зависимая;

2 любой вектор пространства может быть представлен в виде линейной комбинации векторов базиса.

Из определения следует, что это система конечная. В базис входит максимально возможное количество линейно независимых векторов данного пространства.

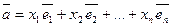
Коэффициенты в разложении вектора по векторам базиса называются координатами вектора в данном базисе.

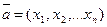
Теорема (о единственности координат вектора в данном базисе)

Координаты вектора в данном базисе определяются однозначно.