Как вычислить объем тела вращения с помощью определенного интеграла?

Кроме нахождения площади плоской фигуры с помощью определенного интеграла (см. 7.2.3.)важнейшим приложением темы является вычисление объема тела вращения. Материал простой, но читатель должен быть подготовленным: необходимо уметь решать неопределенные интегралысредней сложности и применять формулу Ньютона-Лейбница в определенном интеграле, нужны также уверенные навыки построения чертежей. Вообще в интегральном исчислении много интересных приложений, с помощью определенного интеграла можно вычислить площадь фигуры, объем тела вращения, длину дуги, площадь поверхности тела и многое другое. Представьте некоторую плоскую фигуру на координатной плоскости. Представили? ... Теперь данную фигуру можно ещё и вращать, причем вращать двумя способами:

– вокруг оси абсцисс ;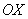

– вокруг оси ординат .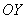

Разберём оба случая. Особенно интересен второй способ вращения, он вызывает наибольшие затруднения, но на самом деле решение практически такое же, как и в более распространенном вращении вокруг оси абсцисс. Начнем с наиболее популярной разновидности вращения.

Вычисление объема тела, образованного вращением плоской фигуры вокруг оси OX

Пример 1

Вычислить объем тела, полученного вращением фигуры, ограниченной линиями 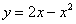, 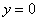вокруг оси .

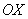Решение:Как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. То есть, на плоскости XOY необходимо построить фигуру, ограниченную линиями 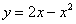, , 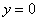при этом не забываем, что уравнение 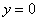задаёт ось 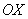. Чертёж здесь довольно прост:

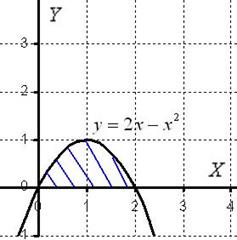
Искомая плоская фигура заштрихована синим цветом, именно она и вращается вокруг оси 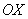. В результате вращения получается такая немного яйцевидная летающая тарелка с двумя острыми вершинами на оси OX, симметричная относительно оси OX. На самом деле у тела есть математическое название, посмотрите в справочнике.

Как вычислить объем тела вращения? Если тело образовано в результате вращения вокруг осиOX, его мысленно разделяют на параллельные слои малой толщины dx, которые перпендикулярны оси OX. Объём всего тела равен, очевидно, сумме объёмов таких элементарных слоёв. Каждый слой, как круглая долька лимона, - низенький цилиндр высотой dx и с радиусом основания f(x). Тогда объём одного слоя есть произведение площади основания πf ² на высоту цилиндра (dx), или π∙f ²(x)∙dx. А площадь всего тела вращения есть сумма элементарных объёмов, или соответствующий определённый интеграл. Объем тела вращения можно вычислить по формуле:

.

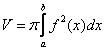Как расставить пределы интегрирования «а» и «бэ», легко догадаться из выполненного чертежа. Функция 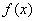… что это за функция? Давайте посмотрим на чертеж. Плоская фигура ограничена графиком параболы 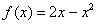сверху. Это и есть та функция, которая подразумевается в формуле. В практических заданиях плоская фигура иногда может располагаться и ниже оси OX. Это ничего не меняет – функция в формуле возводится в квадрат: f ²(x), таким образом, объем тела вращения всегда неотрицателен, что весьма логично. Вычислим объем тела вращения, используя данную формулу:

.

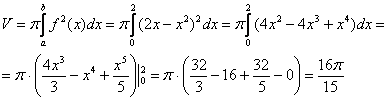Как мы уже отмечали, интеграл почти всегда получается простой, главное, быть внимательным.

Ответ: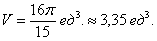

В ответе нужно обязательно указать размерность – кубические единицы 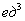. То есть, в нашем теле вращения примерно 3,35 «кубиков». Почему именно кубические единицы? Потому что это наиболее универсальная формулировка. Могут быть кубические сантиметры, могут быть кубические метры, могут быть кубические километры и т.д., это уж, сколько зеленых человечков ваше воображение поместит в летающую тарелку.

Пример 2

Найти объем тела, образованного вращением вокруг оси OX фигуры, ограниченной линиями , , .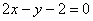

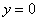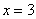Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Пример 3

Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиям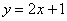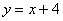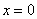и , , и .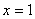

Решение:Изобразим на чертеже плоскую фигуру, ограниченную линиями 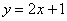, , 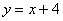, , 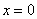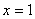не забывая при этом, что уравнение x = 0 задает ось OY:

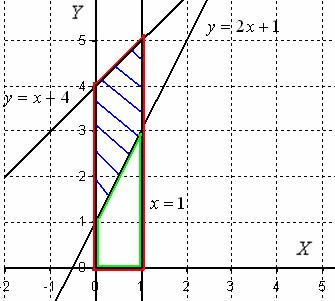
Искомая фигура заштрихована синим цветом. При её вращении вокруг оси OX получается плоский угловатый бублик (шайба с двумя коническими поверхностями).

Объем тела вращения вычислим как разность объемов тел. Сначала рассмотрим фигуру, которая обведена красным цветом. При её вращении вокруг оси OX получается усеченный конус. Обозначим объем этого усеченного конуса через V₁.

Рассмотрим фигуру, которая обведена зеленым цветом. Если вращать данную фигуру вокруг оси OX, то получится тоже усеченный конус, только чуть поменьше. Обозначим его объем через V₂.

Очевидно, что разность объемов, V = V₁ - V_2, - это объем нашего «бублика».

Используем стандартную формулу для нахождения объема тела вращения:

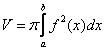
1) Фигура, обведенная красным цветом ограничена сверху прямой 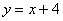, поэтому:

.

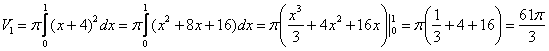2) Фигура, обведенная зеленым цветом ограничена сверху прямой 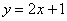, поэтому:

.

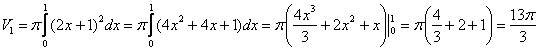3) Объем искомого тела вращения: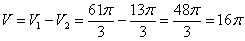

Ответ: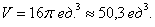

Любопытно, что в данном случае решение можно проверить, используя школьную формулу для вычисления объема усеченного конуса.

Само решение чаще оформляют короче, примерно в таком духе: