Исследование функции на непрерывность

Пусть функция 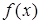определена на интервале 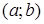, содержащем точку 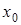, за исключением, быть может, самой точки .

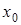Точка 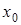, в которой не выполняется хотя бы одно из условий непрерывности функции, называется точкой разрыва функции. Точки разрыва бывают двух типов.

Точка 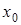называется точкой разрыва I-го рода, если функция не определена в ней, но существуют конечные односторонние пределы 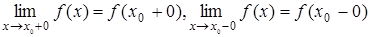. При этом, если 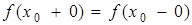, то точка 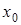– точка устранимого разрыва. Если односторонние пределы не равны между собой, то есть 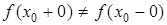, то – то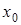чка разрыва I-го рода типа "конечного скачка". Число 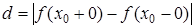называется скачком функции в точке .

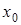Точка 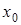называется точкой разрыва II-го рода, если хотя бы один из односторонних пределов не существует или равен бесконечности.

Схема исследования функции на непрерывность:

1) Найти область определения функции, точки разрыва.

2) Определить тип точек разрыва.

3) Определить характер разрыва в точках разрыва I-го рода.

4) Найти вертикальные асимптоты 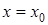, если 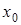–точка разрыва II-го рода.

5) Найти, если есть, горизонтальные асимптоты графика функции 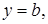где .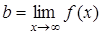

6) Построить эскиз графика функции хотя бы в окрестности точек разрыва, если затруднительно построить его в целом.

Пример12. Исследовать на непрерывность функции

а) 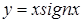; б) 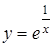и построить эскизы их графиков.

Решение.

а) Так как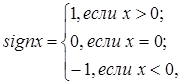

то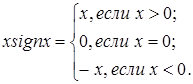

Функция определена на всей числовой оси. Подозрительной на разрыв точкой является точка 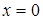. Найдем односторонние пределы функции в этой точке: 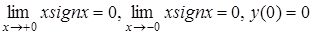, следовательно, функция непрерывна как при 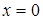, так и при всех других значениях 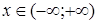. Вертикальных асимптот нет, так как нет точек разрыва II-го рода. Горизонтальных асимптот нет тоже, поскольку 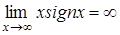. График функции изображен на рис.1.

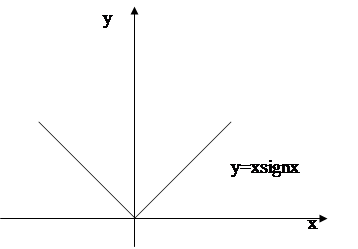Рис.1.

б) 1. Область определения функции D: 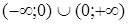, 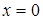– точка разрыва, так как 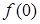не определена.

2. Найдем пределы слева и справа, чтобы определить тип точки разрыва:

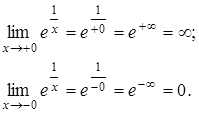
Итак, 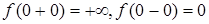, значит, 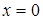– точка разрыва II -го рода.

3. 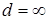– скачок функции.

4. 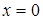– вертикальная асимптота графика функции, так как .

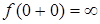5. 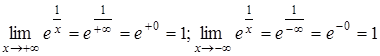, следовательно, 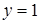– горизонтальная асимптота.

Эскиз графика функции имеет вид:

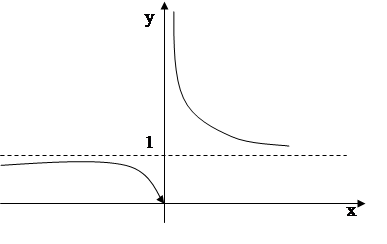Рис.2.

Вопросы к теории:

1. Действительные числа. Свойства действительных чисел.

2. Функция. Примеры функций.

3. Понятие предела функции в точке. Геометрический смысл предела функции.

4. Теорема об ограниченности функции, имеющей предел.

5. Теорема о переходе к пределу в неравенствах

6. Теорема о пределе промежуточной функции.

7. Теорема об арифметических операциях над пределами.

8. Понятие сложной функции. Теорема о замене переменной для пределов функции.

9. Предел функции в бесконечности. Неопределенности.

10. Понятие числовой последовательности и ее предела.

11. Теореме о пределе монотонной ограниченной последовательности. Число е. Натуральные логарифмы.

12. Теорема Больцано - Вейерштрасса.

13. Непрерывность функции в точке. Теорема о непрерывности суммы, произведения, частного непрерывных функций.

14. Непрерывность основных элементарных функций. Гиперболические функции, их графики.

15. Теорема о непрерывности сложной функции.

16. Обратная функция, теорема о существовании непрерывной обратной функции.

17. Первый замечательный предел.

18. Бесконечно малые функции и их основные свойства.

19. Второй замечательный предел.

20. Теорема о связи между функцией, ее пределом и бесконечно малой.

21. Бесконечно большие функции. Связь между бесконечно малыми и бесконечно большими функциями.

22. Сравнение бесконечно малых функций.

23. Условие эквивалентности бесконечно малых функций.

24. Таблица эквивалентностей.

25. Теорема об эквивалентных бесконечно малых, применяемая при вычислении пределов.

26. Классификация разрывов функции. Схема исследования функций на непрерывность.

Упражнения:

1. Доказать эквивалентность неравенств: .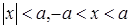

2. Доказать, что для любых 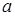и 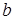имеют место неравенства: .

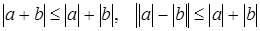3. Доказать, что если 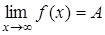, то .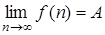

4. Доказать, что отбрасывание или замена конечного числа членов последовательности не влияют на сходимость последовательности, причем в случае сходящейся последовательности не влияют на величину предела.

5. Пусть 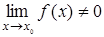, а 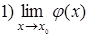не существует, 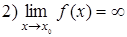. Что можно сказать о 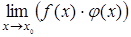в каждом из этих случаев?

6. Пусть 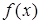имеет предел в точке 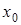, а функция 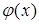не имеет предела в этой точке. Будут ли существовать пределы: 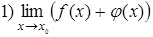, 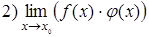. Рассмотреть пример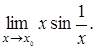

7. При каких значениях 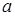функция 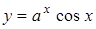будет не ограничена при ?

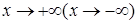8. Функцию 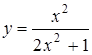, имеющую предел при 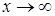, представить в виде суммы постоянной величины и некоторой функции, бесконечно малой при .

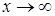9. Доказать, что если 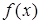– непрерывная функция, то функция 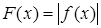также непрерывная. Верно ли обратное утверждение?

10. Исследовать непрерывность функции Дирихле.