В.7. Непрерывность функции
Функция f(x) называется непрерывной в точке х0, если она удовлетворяет следующим условиям:
1) она определена в точке х0,, т.е. существует f(х0);
2) она имеет конечный предел функции при х ® х0 ( 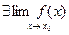 );
);
3) этот предел равен значению функции в точке х0, т.е. 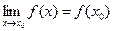
Пример 6. А) Функция 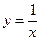 в точке х = 0 не является непрерывной (нарушено 1-е условие).
в точке х = 0 не является непрерывной (нарушено 1-е условие).
Б) Функция, заданная выражением: 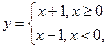 в точке х = 0 не является непрерывной из-за отсутствия предела при х ® 0, хотя существуют пределы слева и справа (нарушено 2-е условие).
в точке х = 0 не является непрерывной из-за отсутствия предела при х ® 0, хотя существуют пределы слева и справа (нарушено 2-е условие).
В) 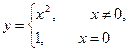 - не является непрерывной, т.к. нарушено 3-е условие.
- не является непрерывной, т.к. нарушено 3-е условие.
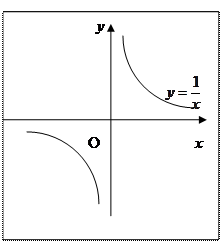
Г) Функция y = x2 является непрерывной в точке х = 0.
 |   y 1_ y 1_ 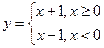  x x  1_ 1_ | 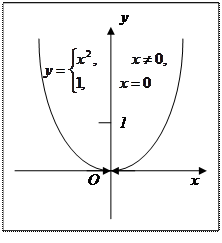 |
Непрерывность функции f(x) в точке х0 можно записать и так:
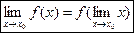
т.е. для непрерывной функции возможна перестановка символов предела и функции.
Другое определение непрерывности: функция y = f(x) называется непрерывной в точке х0, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: 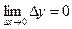
Оба определения равносильны.
Точка х0 называется точкой разрыва функции f(x), если эта функция в данной точке не является непрерывной. Существует две разновидности точек разрыва.
Точка разрыва 1-го рода: существуют конечные односторонние пределы функции слева и справа при х ® х0, не равные друг другу.
В качестве примера можно указать точку х = 0 для функции 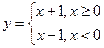 .
.
Точка разрыва 2-го рода: хотя бы один из односторонних пределов равен бесконечности или не существует.
В качестве примера можно указать точку х = 0 для функции 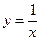 .
.
Свойства функций непрерывных в точке:
1. Если функции f(x) и j (х) непрерывны в точке х0, то их сумма f(x) + j(х), произведение f(x) × j(х) и частные 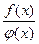 (j(х) ¹ 0) являются функциями, непрерывными в точке х0.
(j(х) ¹ 0) являются функциями, непрерывными в точке х0.
2. Если функция y = f(x) непрерывна в точке х0 и f(x0) > 0, то существует такая окрестность точки x0, в которой и f(x) > 0.
3. Если функция y = f(u) непрерывна в точке u0 и f(x0) > 0, а функция u = j(х) непрерывна в точке х0, то сложная функция y = f[j(х)] непрерывна в точке х0 .
Функция y = f(x) называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка.
Свойства функций непрерывных на отрезке:
1. Если функция y = f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке.
2. Если функция y = f(x) непрерывна на отрезке [a, b], она достигает на этом отрезке наименьшего значения m и наибольшего значения M.
3. Если функция y = f(x) непрерывна на отрезке [a, b] и ее значения на концах отрезка f(a) и f(b) имеют противоположные знаки, то внутри отрезка найдется точка x Î (a, b) такая, что f(x)=0.
В.8. Вычисление пределов
При вычислении пределов используют то, что предел постоянной равен самой постоянной, а также основные теоремы о пределах. Рассмотрим вычисление пределов на примерах.
Приме7. 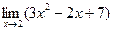
Применяя теоремы о пределах, получаем:
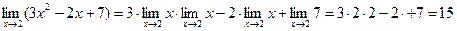
Пример 8. 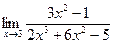
Пределы числителя и знаменателя существуют и предел знаменателя не равен нулю. Пользуясь теоремой о пределе частного, получаем:
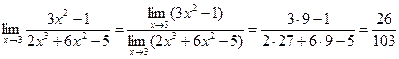
Пример 9. 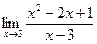
Непосредственно применять теорему о пределе частного нельзя, т.к. предел знаменателя равен нулю. В числителе имеем ограниченную величину, отличную от нуля. Таким образом, под знаком предела будет произведение ограниченной величины х2-2х+1, отличной от нуля на бесконечно большую величину 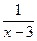 при х ® 3 как величину, обратную бесконечно малой. Поэтому
при х ® 3 как величину, обратную бесконечно малой. Поэтому 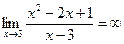
Пример 10. 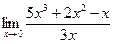
Здесь также нельзя непосредственно применять теорему о пределе частного, т.к. пределы знаменателя и числителя равны нулю и мы имеем неопределенность вида 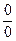 . В подобных случаях, когда и в числителе и в знаменателе – многочлены, их необходимо разложить на множители, после этого дробь сократить и перейти к пределу:
. В подобных случаях, когда и в числителе и в знаменателе – многочлены, их необходимо разложить на множители, после этого дробь сократить и перейти к пределу:
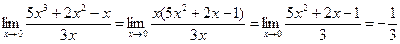

Пример 11. 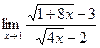
Если под знаком предела имеется иррациональность, то для раскрытия неопределенности вида 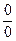 необходимо перенести иррациональность из числителя в знаменатель или из знаменателя в числитель, а иногда и то и другое, полученную дробь сократить и перейти к пределу:
необходимо перенести иррациональность из числителя в знаменатель или из знаменателя в числитель, а иногда и то и другое, полученную дробь сократить и перейти к пределу:
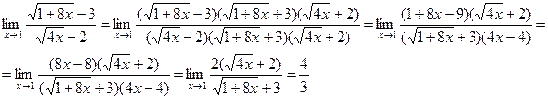
Пример 12. 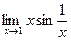
При х ® 0 переменная х есть бесконечно малая величина, а ï 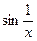 ï£ 1 при любых значениях х¹0. Следовательно, величина
ï£ 1 при любых значениях х¹0. Следовательно, величина 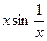 - произведение бесконечно малой на ограниченную величину – также будет бесконечно малой величиной, поэтому ее предел равен 0.
- произведение бесконечно малой на ограниченную величину – также будет бесконечно малой величиной, поэтому ее предел равен 0.
Пример 13. 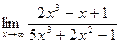
Теорему о переделе частного здесь применять нельзя, т.к. числитель и знаменатель конечного предела не имеют. Имеем неопределенность 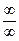 . В подобных случаях для раскрытия неопределенности целесообразно числитель и знаменатель разделить на степень х с наивысшим показателем, а затем перейти к пределу:
. В подобных случаях для раскрытия неопределенности целесообразно числитель и знаменатель разделить на степень х с наивысшим показателем, а затем перейти к пределу:
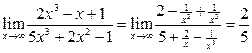
Неопределенность вида ¥ – ¥ раскрывается путем преобразования и сведения их к неопределенности 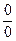 или
или 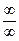 .
.
Пример 14. 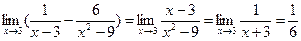
Пример 15. 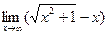
Здесь следует рассмотреть два случая:
а) 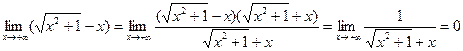
б) 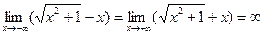
Если при х ® а (х ® ¥) f(x) ® 1, а j(х) ® ¥, то говорят, что имеем неопределенность вида 1¥. Для раскрытия этой неопределенности используется второй замечательный предел.
Пример 16. Найти 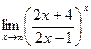 .
.
Решение. Выделим у дроби целую часть:
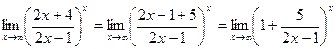 .
.
Чтобы использовать второй замечательный предел 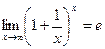 (или
(или 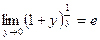 ), обозначим
), обозначим 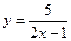 . Тогда при х→∞ у→0, причем
. Тогда при х→∞ у→0, причем 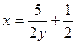 . Т.о.
. Т.о. 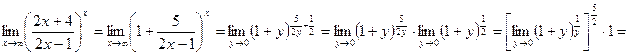 =
= 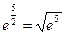 .
.
Ответ: 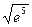 .
.
