Асимптоты графика функции
Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.
Определение 7.1 Вертикальной асимптотой графика функции 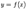 называется вертикальная прямая
называется вертикальная прямая  , если
, если 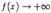 или
или 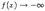 при каком-либо из условий:
при каком-либо из условий: 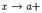 ,
,  ,
,  . Заметим, что мы при этом не требуем, чтобы точка
. Заметим, что мы при этом не требуем, чтобы точка 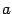 принадлежала области определения функции
принадлежала области определения функции 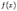 , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки:
, однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки: 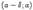 или
или 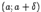 , где
, где 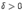 .
.
Наклонной асимптотой графика функции 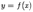 при
при 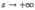 называется прямая
называется прямая 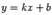 , если выполнены два условия:
, если выполнены два условия:
1) некоторый луч 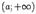 целиком содержится в
целиком содержится в 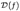 ;
;
2) расстояние по вертикали между графиком и прямой стремится к 0 при 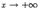 :
:
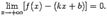 | (7.1) |
Наклонной асимптотой графика функции 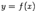 при
при 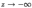 называется прямая
называется прямая  , если
, если
1) некоторый луч  целиком содержится в
целиком содержится в 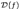 ;
;
2) расстояние по вертикали между графиком и прямой стремится к 0 при 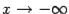
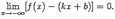
В случае, если наклонная асимптота расположена горизонтально, то есть при  , она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота -- частный случай наклонной асимптоты; прямая
, она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота -- частный случай наклонной асимптоты; прямая 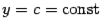 является горизонтальной асимптотой графика
является горизонтальной асимптотой графика 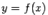 при
при 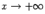 или
или 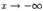 , если
, если 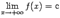 или
или 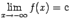 соответственно.
соответственно.
53ВОПРОСОбщая схема исследования функции и построения её графика.
При построении графиков функций более сложного вида можно примерно придерживаться следующего плана.
1. Найти область определения и область значений функции.
2. Выяснить, является ли функция четной (нечетной).
3. Выяснить, является ли функция периодической.
4. Найти точку пересечения графика функции с осью ординат.
5. Найти нули функции и промежутки знакопостоянства.
6. Вычислить производную функции 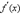 и определить точки, в которых могут существовать экстремумы.
и определить точки, в которых могут существовать экстремумы.
7. Найти промежутки монотонности функции.
8. Определить экстремумы функции.
9. Вычислить вторую производную 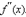
10. Определить точки перегиба.
11. Найти промежутки выпуклости функции.
12. Найти асимптоты графика.
13. Найти значения функции в нескольких контрольных точках.
14. Построить эскиз графика функции.
54ВОПРОСКривизна плоской кривой. Радиус кривизны. Понятие об эволюте и эвольвенте.
Плоскую кривую линию можно рассматривать как траекторию движения точки в плоскости; точка движется по касательной к кривой линии, обкатывая эту кривую без скольжения.
Движение точки вдоль кривой а связано с непрерывным изменением двух величин: расстояния S, на которое удалена точка от начального положения и углаa поворота касательной относительно начального положения.
Если с увеличением пути S непрерывно увеличивается и a , кривая называется простой.
Угол a (угол смежности) между касательными в двух бесконечно близких точках кривой, отнесенный к длине дуги между этими точками, определяет степень искривленности кривой линии, т.е. определяеткривизнукривой k.
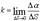 ,
,
предел отношения угла смежности касательных к соответствующей дуге.
Кривизна прямой в любой её точке равна нулю.
Кривизна произвольной кривой линии в различных точках различна, в отдельных точках она может быть равна нулю. Такие точки называются точками спрямления.
Кривизна в каждой из точек плоской кривой а определяется с помощью соприкасающейся в этой точке окружности
Соприкасающейся окружностью или кругом кривизны в данной точке называется предельное положение окружности, когда она проходит через данную точку и две другие бесконечно близкие к ней точки.
Центр соприкасающейся окружности называется центром кривизны кривой в данной точке, а радиус такой окружности – радиусом кривизны кривой линии в данной точке.
Множеством центров кривизны кривой является кривая линия - её называют эволютой данной кривой, а кривая по отношению к своей эволюте называется эвольвентой.
55ВОПРОСВекторная функция скалярного аргумента: определение, предел, непрерывность. Дифференцирование векторной функции. Геометрический и механический смысл производной.
