Отображения множеств (функции). Предел и непрерывность функции в точке. Свойства непрерывных функций в точке

Отображением множества E в множество F, или функцией, определенной на E со значениями в F, называется правило, или закон f, который каждому элементу 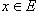ставит в соответствие определенный элемент .

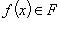Элемент 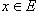называют независимым элементом, или аргументом функции f, элемент 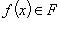называют значением функции f, или образом; при этом элемент 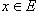называется прообразом элемента .

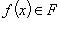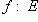
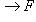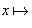
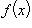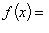
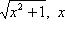
Отображение (функцию) обычно обозначают буквой f или символом , указывая тем самым, что f отображает множествоE в F. Употребляется также обозначение , указывающее, что элементу x соответствует элемент f(x). Иногда функцию удобно задавать посредством равенства, в котором содержится закон соответствия. Например, можно говорить, что "функция f определена равенством 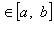". Если "y" - общее наименование элементов множества F, т. е. F = {y}, то отображение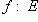 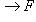записывают в виде равенства y = f(x) и говорят, что это отображение задано явно.

Функция у = f (х) называется непрерывной в точке х₀, если в этой точке бесконечно малому приращению аргумента х-х₀= х соответствует бесконечно малое приращение функции

у—у₀ = у, т. е. если

lim y = lim [ f (х₀ + х) – f (х₀)] = 0.

Этому определению равносильно следующее:

Функция f (х) называется непрерывной в точке х₀, если при х—> х₀ предел функции существует и равен ее частному значе­нию в этой точке, т. е. если limf(х) = f (x₀).

x->х₀

Для непрерывности функции f(х) в точке х₀ необходимо и достаточно выполнение следующих условий:

1)функция должна быть определена в некотором интервале, содержащем точку х_0.(т. е. в самой точке х₀ и вблизи этой точки);

2) функция должна иметь одинаковые односторонние пределы

lim f (х) = lim f (x);

x->х₀ -0 x->х₀ +0

3) эти односторонние пределы должны быть равны f (x₀).

Функция f (x) называется разрывной в точке х₀, если она опре­делена в сколь угодно близких точках, но в самой точке х₀ не удовлетворяет хотя бы одному из условий непрерывности.

Разрыв функции f(х) в точке х₀ называется конечным, или 1-го рода, если существуют конечные односторонние пределы

lim f(x) и lim f(х).

x-> х₀ -0 x-> х₀ +0

Все другие случаи разрыва функции называются разрывами- 2-го-рода; в частности, если хотя бы один из указанных односторонних пределов окажется бесконечным, то и разрыв функции называется бесконечным.

Определение.

Число b называется пределом функцииy = f(x) при х→+∞, если для любого числа ε > 0 найдётся такое число М > 0, что для всех х > М выполняется неравенство |f(x) –b|< ε.

Записывают так:

lim_х→+∞ f(x) = b.

Геометрически это означает, что график функции y = f(x) при выборе достаточно больших значений хбезгранично приближается к прямой у = b. Это означает, что расстояние от точки графика до прямой у = b по мере удаления точки в бесконечность может быть сделано меньше любого числа ε > 0. Прямая называется в этом случае горизонтальной асимптотой графика функции y = f(x).

Например: lim_х→+∞ 1/х = 0 и функция y = 1/химеет горизонтальную асимптоту у = 0.

Определение.

Число b называется пределом функции y = f(x) при х→–∞, если для любого числа ε > 0 найдётся такое число М > 0, что для всех х < –М выполняется неравенство |f(x) –b|< ε.

Записывают так:

lim_х→–∞ f(x) = b.

В этом случае прямая y = b также является горизонтальной асимптотой функции y=f(x), график которой бесконечно близко приближается к ней при достаточно больших по модулю, но отрицательных значениях х.

Например: lim_х→–∞ (3 + 2^х) = 3 и функция y = (3 + 2^х) имеет горизонтальную асимптоту у = 3.

Наконец, прямая у = b может быть горизонтальной асимптотой графика функции и при х→+∞, и прих→–∞. Пишут так: х→∞.

Определение.

Числоb называется пределом функцииy=f(x) при х → ∞, если для любого числа ε > 0 найдётся такое число М > 0, что для всех x таких, что |х| > М, выполняется неравенство |f(x) –b|<ε.

Записывают так:

lim _х→∞ f(x) = b.

Например: lim _х→∞ х²/(х²+1) = 1 и функция y = х²/(х²+1) имеет горизонтальную асимптоту у = 1.

Свойства функций, непрерывных в точке:

1. Если функции f(x) и φ(x) непрерывны в точке х₀, то их сумма f(x)+φ(x), произведение f(x)φ(x) и частное 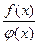(при условии 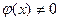) являются функциями, непрерывными в точке х_0.

2. Если функция у=f(x) непрерывна в точке х₀ и f(х₀)>0, то существует такая окрестность точки х₀, в которой f(х)>0.

3. Если функция f(и)>0 непрерывна в точке и₀, а функция и= φ(x) непрерывна в точке и₀= φ(x₀), то сложная функция у= f(φ(x)) непрерывна в точке х₀.

Свойство 3 может быть записано в виде 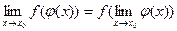, т.е. под знаком непрерывной функции можно переходить к пределу.

Функция у=f(x) называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка. Все элементарные функции непрерывны в области их определения.

Элементарные функции и их непрерывность. Свойства непрерывных функций на отрезке.