Приложение теории к решению задач

I. Построить кривую 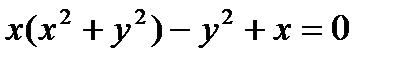(а)

Решение. Искомое уравнение содержит только один член с третьей степенью и этот член имеет коэффициентом единицу. Следовательно, нет асимптот, параллельных оси х. Действительно, деля на х³, получим:

.

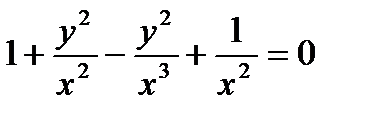Переходя к пределу 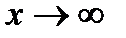и предполагая, что при этом у со­храняет конечное значение, придем к невозможному равенству 1=0.

Зато уравнение содержит два члена с высшей степенью y². Деля на y² и переходя к пределу 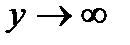предполагая, что х сохраняет конечное значение, получим в пределе .

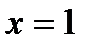Это будет уравнение асимптоты, параллельной оси ординат. Дифференцируя правую часть уравнения

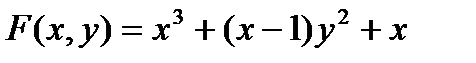
по x и по y, получим

.

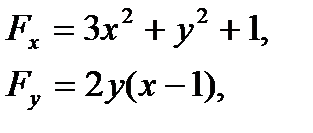
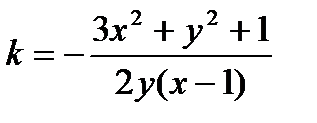Мы видим, что F_x как сумма трех положительных чисел не об­ращается в нуль. Следовательно, кривая не имеет касательных, па­раллельных оси абсцисс.

Производная F_y обращается в нуль при х=1; это соответствует найденной асимптоте. Кроме того, F обращается в нуль и касатель­ная становится параллельной оси у при пересечении оси кривой с осью абсцисс y=0.

Уравнение (а) при этом принимает вид:

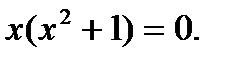
Второй множитель, очевидно, отличен от нуля (сумма положитель­ных чисел), а первый показывает, что кривая пересекает ось абсцисс в начале координат, касаясь, следовательно, оси ординат.

Уравнение (а) может быть разрешено относительно у²:

.

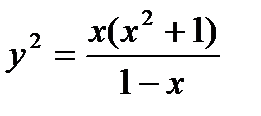Так как в левой части стоит квадрат, то правая часть должна быть положительна. Второй множитель числителя, x²+1, всегда положи­телен. Значит, должно быть:

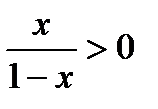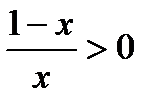или , или .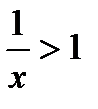

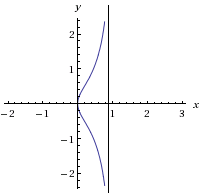Рисунок 6

Отсюда следует, что х не может быть отрицательным (ибо отри­цательное число — меньше всякого положительного числа) и, значит, x<1 (чтобы 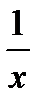было больше единицы).

Итак, кривая существует только для зна­чений х в интервале

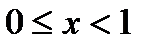(рис. 6)

Следовательно, абсцисса х не может расти до бесконечности.

II. Построить график функции 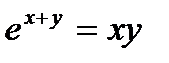,заданной неявно

Решение. Рассмотрим такую функцию 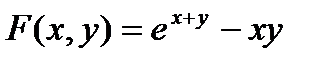. Частная производная F по x равна .

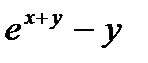При y > 0: производная больше нуля при 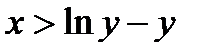, и меньше нуля при 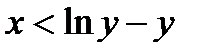,т.е. 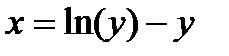точка минимума. Найдем значение F в точке минимума 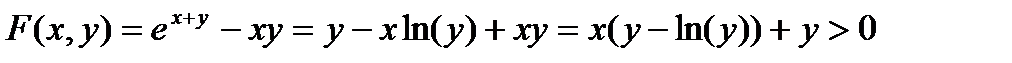. Это значит при y > 0 будет F(x,y) > 0 при всех x, то есть решений у уравнения в области y > 0 нет.

При y=0 равенство обращается 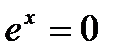. Это уравнение также не имеет решений.

При y < 0: производная функции будет больше нуля при всех x, то есть функция монотонно растёт с ростом x. При больших по модулю отрицательных x функция примерно равно - xy, то есть меньше нуля. При больших по модулю положительных x функция примерно равно 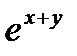, т.е. больше нуля. Следовательно, при любом y < 0 искомое уравнение будет иметь ровно один корень (в силу монотонности F(x,y), корней не может быть больше одного, а в силу того, что F(x,y) меняет знак, хотя бы один корень есть).

В силу того, что 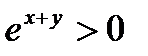корень уравнения при любом y < 0 лежит на диапазоне x < 0.

Далее рассмотрим полный дифференциал функции.

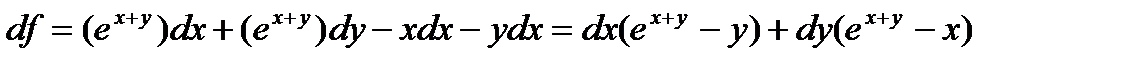
для искомого графика df = 0, т.е. 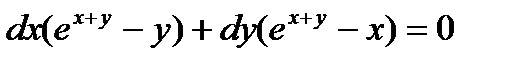. Кроме того, для точек искомого графика 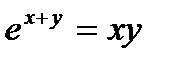значит

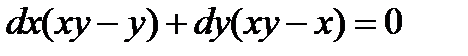
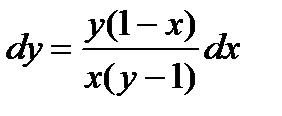
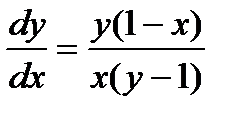
С учётом того, что для всех точек графика x < 0, y < 0 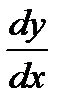отрицательно вычислим вторую производную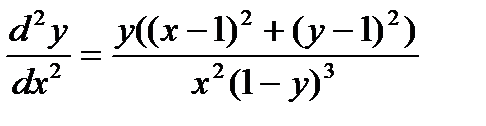

При x < 0, y < 0 это выражение отрицательно. При x стремящемся к минус бесконечности, 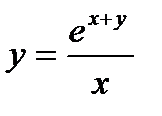стремится к нулю.

Если x достаточно велико по сравнению с y, y будет близко к .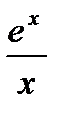

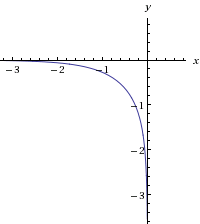
На основании всего вышеизложенного можно сказать о графике следующее

График расположен в третьей четверти

(x < 0, y < 0)

Рисунок 7

График является убывающей функцией

( )

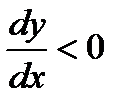График функции является выпуклым вверх

( )

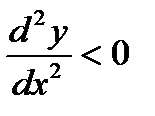В силу симметрии уравнения график является симметричным относительно y=x (рис. 7)

График имеет асимптоту y=0

III. Найти производную неявно заданной функции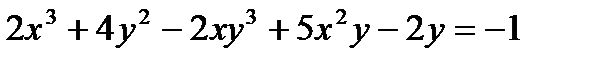

Решение. Продифференцируем обе части данного выражения по х, учитывая, что у функция от х и производная от неё берется как от сложной функции

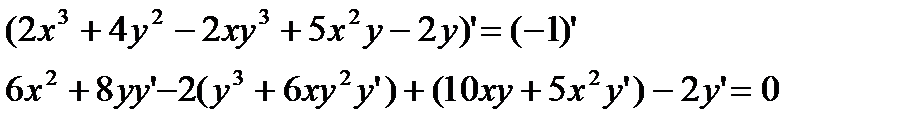
Выразим из этого равенства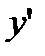

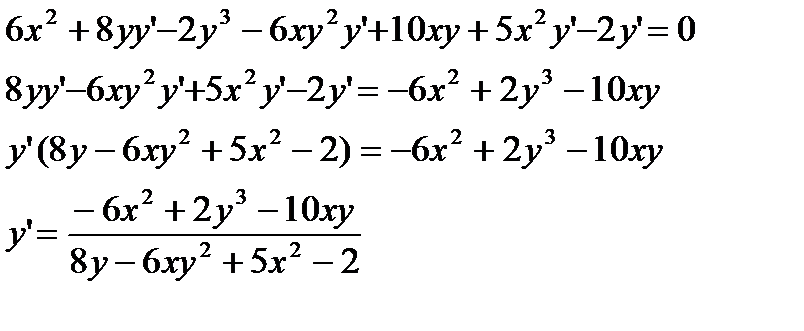
Ответ: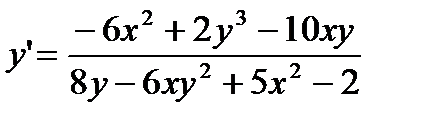

IV. Построить кривую 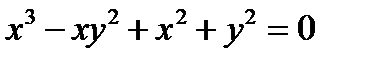(а)

Решение. Так как уравнение кривой не содержит свободного члена и членов первой степени, то начало координат — особая точка. Пара касательных вначале определяется уравнением x²+y²=0. Ка­сательные мнимы. Особая точка — изолированная.

Кривая имеет асимптоту, параллельную оси ординат ( x=1), ибо для этого значения х коэффициент при у² обращается в нуль. Кроме того, она имеет две асимптоты, не параллельные осям коорди­нат. Действительно, если разделить уравнение (а) на x³и перейти к пределу 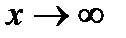, то получим для 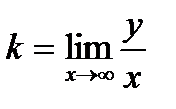уравнение

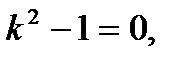т.е.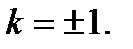

С другой стороны, внося

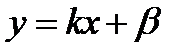
в уравнение (а) и помня, что k² = 1 получим:

,

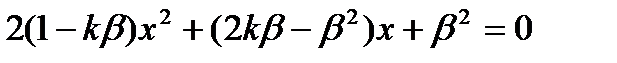откуда пр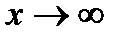и и 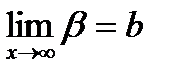имеем:

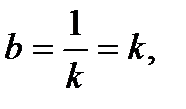ибо .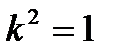

Значит, кривая имеет две асимптоты:

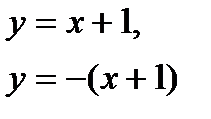
Они пересекают кривую в общей точке x=-1, у=0.

Так как уравнение (а) содержит у только в квадрате, то кривая симметрична относительно оси х. С другой стороны, разрешая уравнение относительно у²

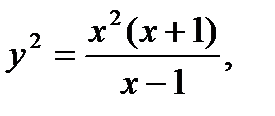
видим, что ордината будет действительной, кроме начала координат, только вне отрезка

,

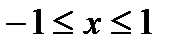единственное исключение — особая точка x=0, у=0, откуда еще раз видно, что эта точка — изолированная.

Дифференцируя, имеем:

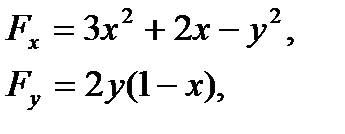
откуда

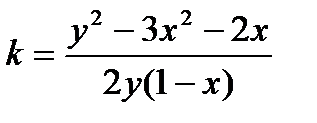
Касательная параллельна оси ординат, если

1) y=0или 2) x=1.

В первом случае мы найдем, кроме особой точки (0, 0), точку пересечения асимптот х=-1, у =0; во втором мы придем к не­собственной точке.

Касательная параллельна оси абсцисс, если

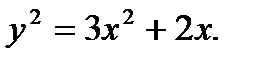
Внося это значение в уравнение (а) и сокращая на х (что соответст­вует исключению особой точки), получим:

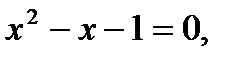
откуда:

.

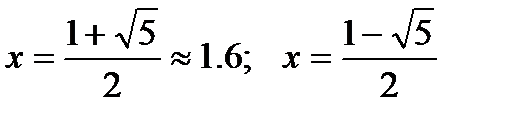Только первый корень приводит к действительному значению орди­наты у.

Имеем таблицу опорных точек (рис. 8):

	x	Y	k
O			Изолированная точка
M1	-1
M2	1.6	3.2

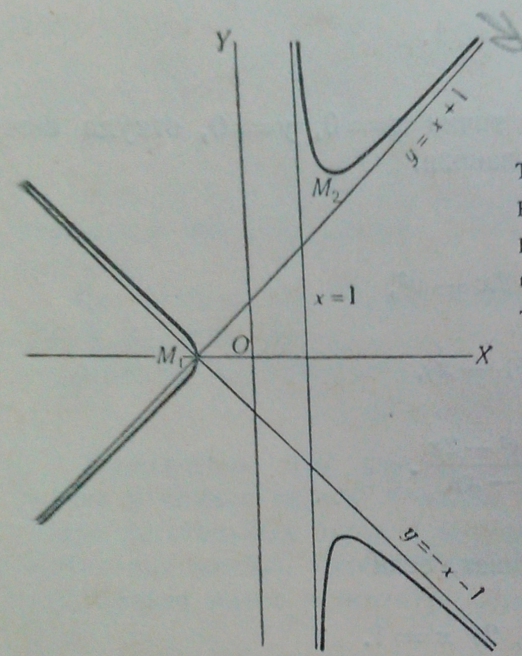
V. Построить кривую 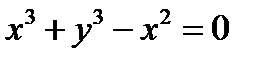(а).

Рисунок 8

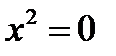Решение. Кривая имеет в начале особую точку. Пара касательных определяется уравнением . Значит, кривая касается оси ординат. Как как члены третьей степени имеются ( 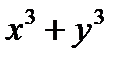) и не делятся на 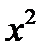, то в начале координат – точка возврата первого рода.

Так как y, очевидно, должно быть положительно, то кривая в окрестности начала лежит выше оси абсцисс.

Кривая имеет асимптоту. Деля уравнение (а) на 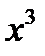и переходя к пределу 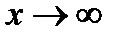, , 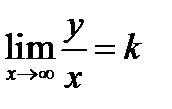получим:

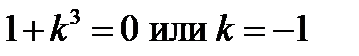
Полагая 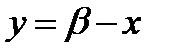и внося в уравнение (а), получим

.

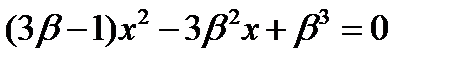Деля на 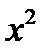и переходя к пределу 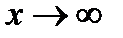, , 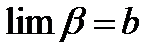получим:

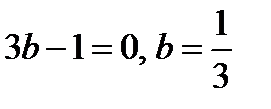
Отсюда асимптота:

.

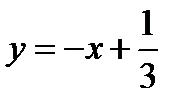Она пересекается с кривой в точке

.

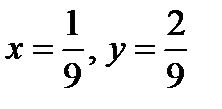Кривая имеет с осью ординат только одну общую точку – особую; ось абсцисс она пересекает еще в точке (1,0).

Дифференцирую, имеем:

.

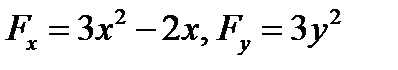Откуда:

.

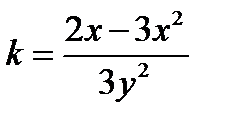Касательная параллельна оси абсцисс в точке

.

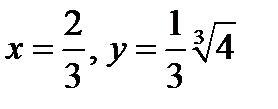Она параллельна оси ординат только в точках пересечения кривой с осью абсцисс.

Имеем таблицу опорных точек (рис. 9)

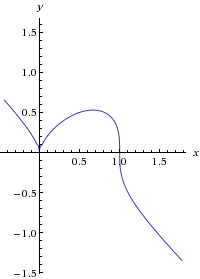Рисунок 9

	x	y	k
O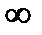
M1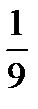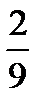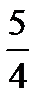
M2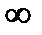
M3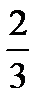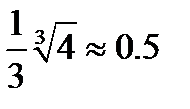

Глава II. Некоторые вопросы методики изучения линий на плоскости в школьном курсе математики.