Прикладзнаходження базисних розв’язків системи лінійних рівнянь матричним методом
Щоб знайти інші базисні розв’язки системи лінійних рівнянь скористаємося більш раціональним способом їх знаходження, а саме матричним методом.
Візьмемо розширену матрицю А коефіцієнтів невідомих та вільних членів системи рівнянь, записану як таблиця у програмі Microsoft Excel.
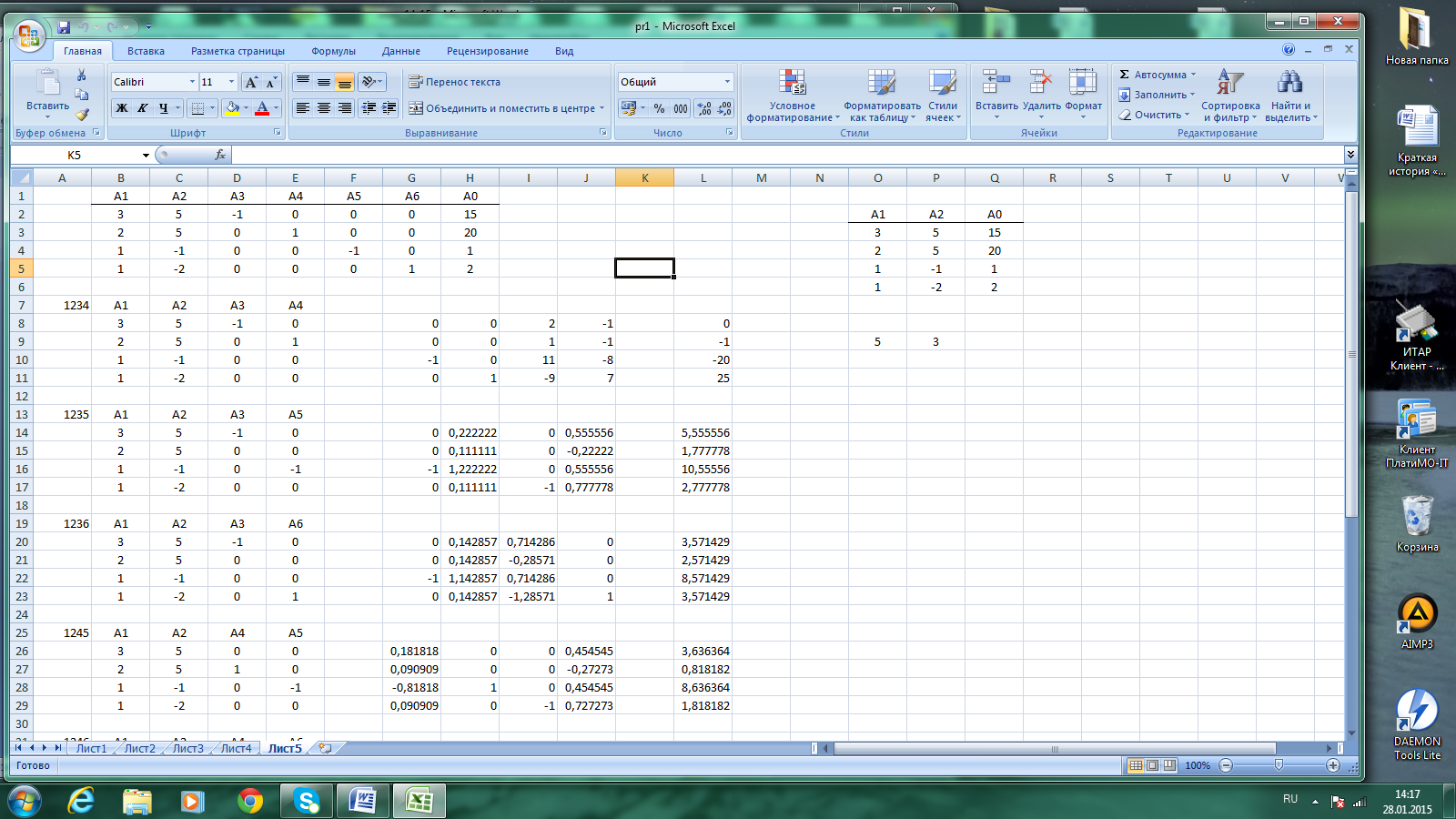
Виберемо чотири стовпчики коефіцієнтів невідомих: х1; х2; х3; х6 та утворимо з них матрицю D, скопіювавши вибрані стовпчики у відповідні вільні клітинки сторінки Microsoft Excel.
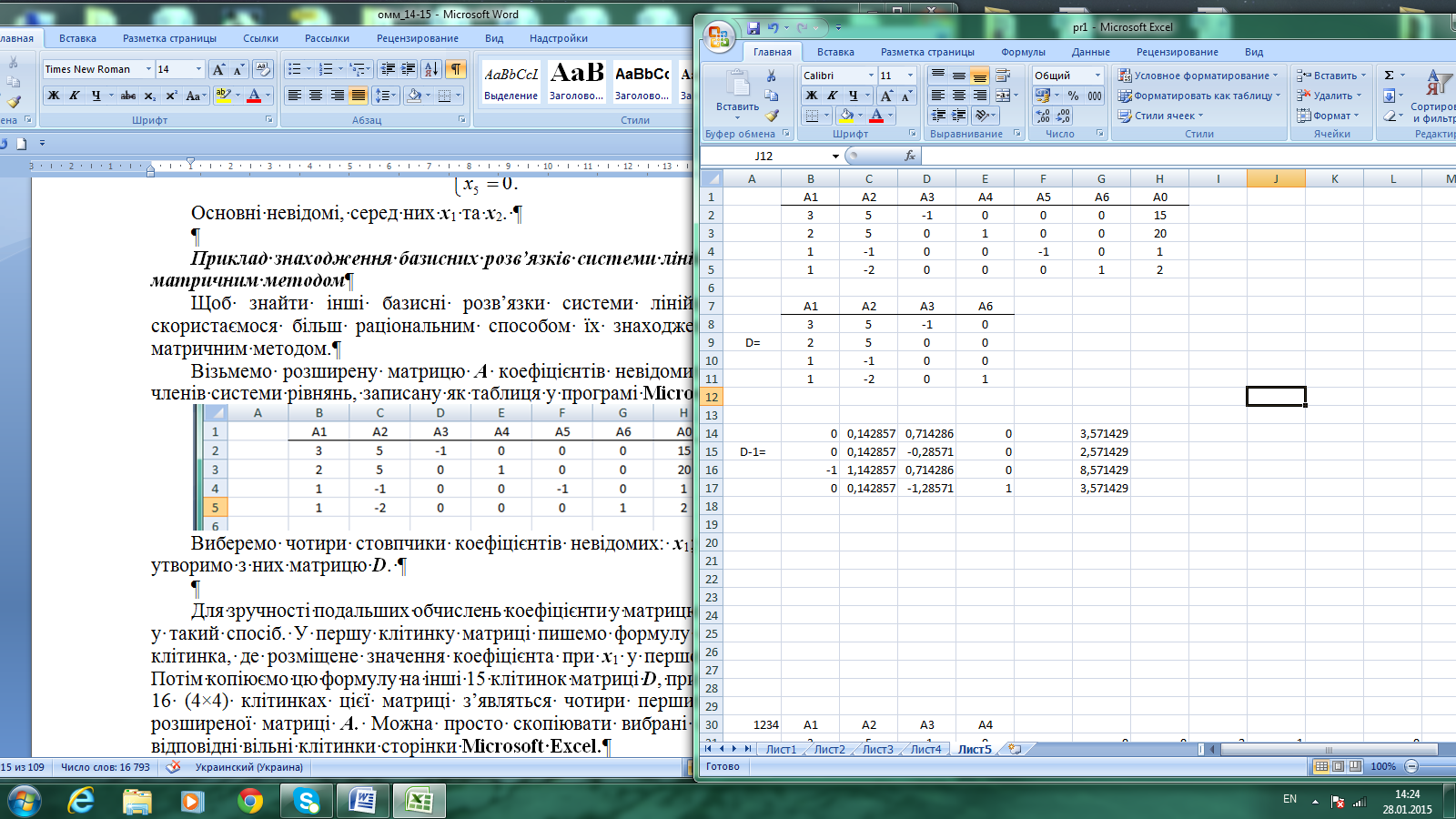
Виберемо та виділимо курсором наступні 16 (4×4) клітинок для обчислення оберненої матриці D-1. Задамо виконання обчислень за допомогою функції «МОБР», виділивши масив значень матриці D та скориставшись командою Ctrl+Shift+Enter, отримаємо числові значення елементів оберненої матриці D-1.
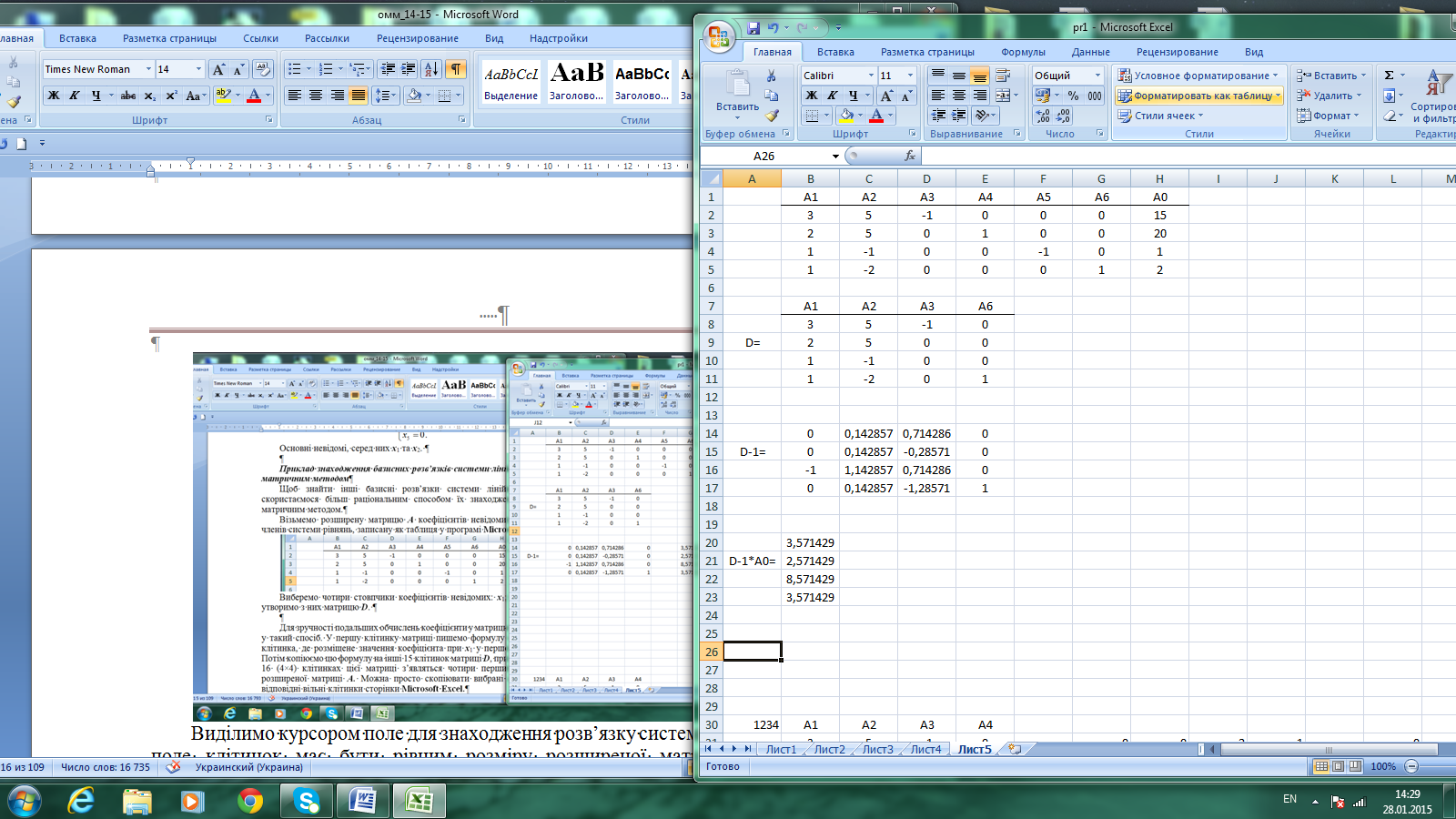
Виділимо курсором поле для знаходження розв’язку системи рівнянь. Це поле клітинок має бути рівним розміру розширеної матриці А. Для наведеного прикладу це поле має розмір 4×7. Далі потрібно знайти добуток матриці D-1 на початкову матрицю А(D-1*А) за допомогою функції «МУМНОЖ», виділивши масиви значень матриці D-1 і матриці А та скориставшись командою Ctrl+Shift+Enter.
У виділеному полі результатів обчислень отримаємо розв’язок задачі для базису х1; х2; х3; х6 – ті самі числові значення, що і для методу Жордана-Гаусса, які читаємо у стовпчику А0. (Числа виду 1,11022Е-16 означають 1,11022*10-16 – їх слід вважати рівними 0).
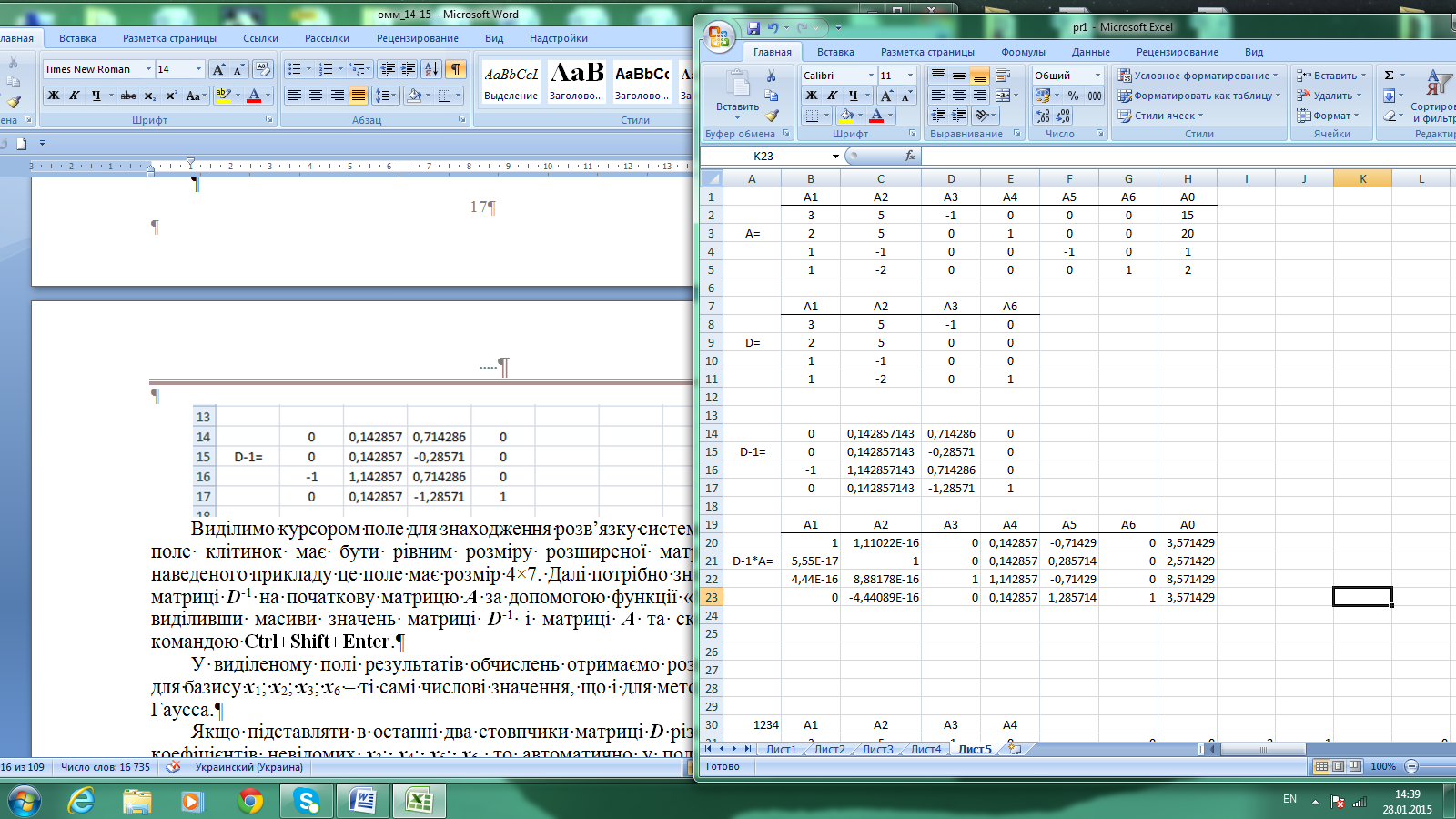
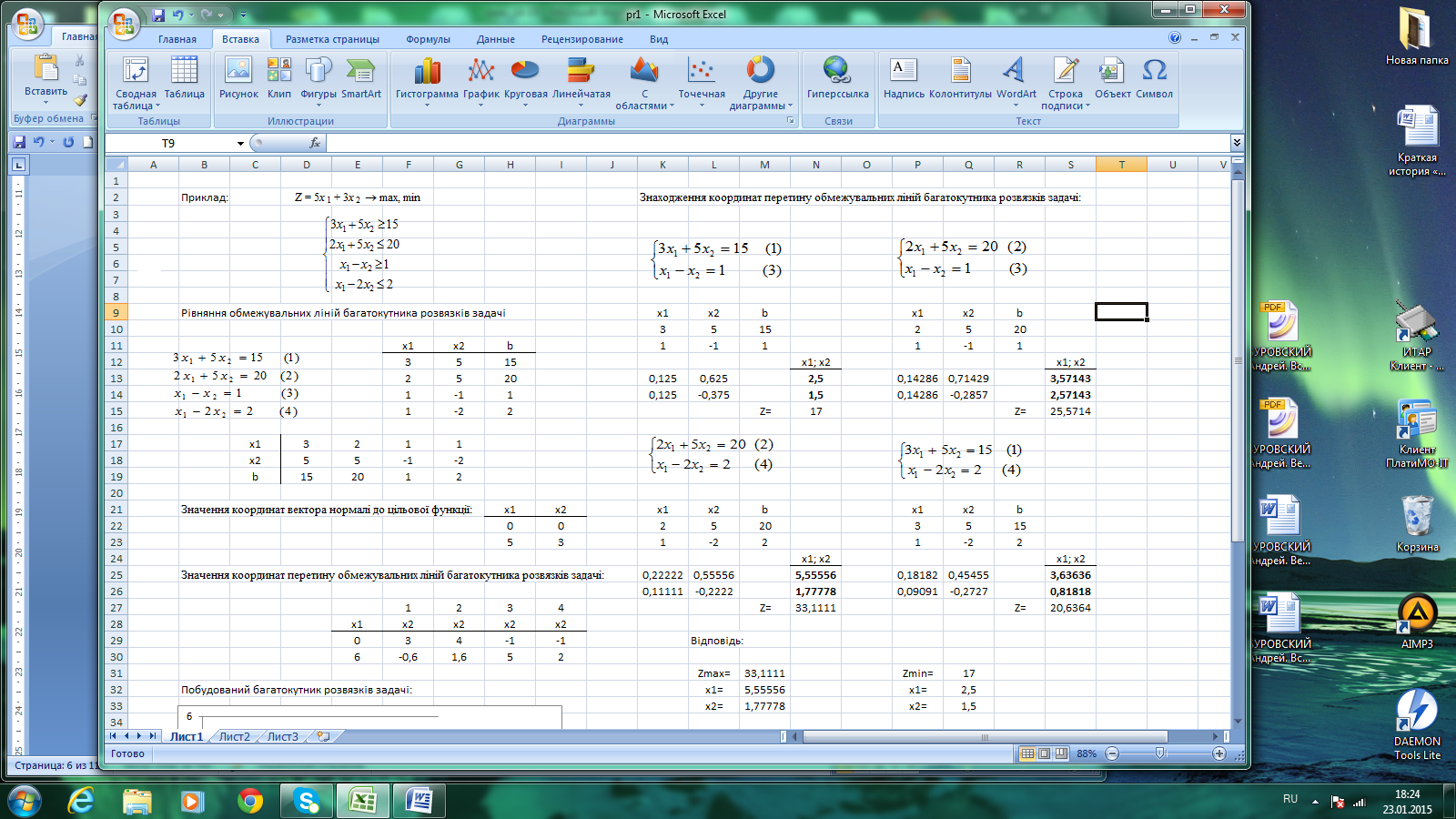
Якщо підставляти в останні два стовпчики матриці D різні комбінації коефіцієнтів невідомих х3; х4; х5; х6, то автоматично у полі результатів обчислень матимемо інші базисні розв’язки задачі, куди обов’язково мають входити основні змінні задачі х1; х2. Для розглядуваного прикладу можливі лише шість комбінацій базисних змінних, які позначимо номерами цих змінних: 1234; 1235; 1236; 1245; 1246; 1256.Для знаходження цих базисних розв’язків зменшимо об’єм обчислень. Для цього достатньо замінити добуток D-1*Адобутком D-1*А0.
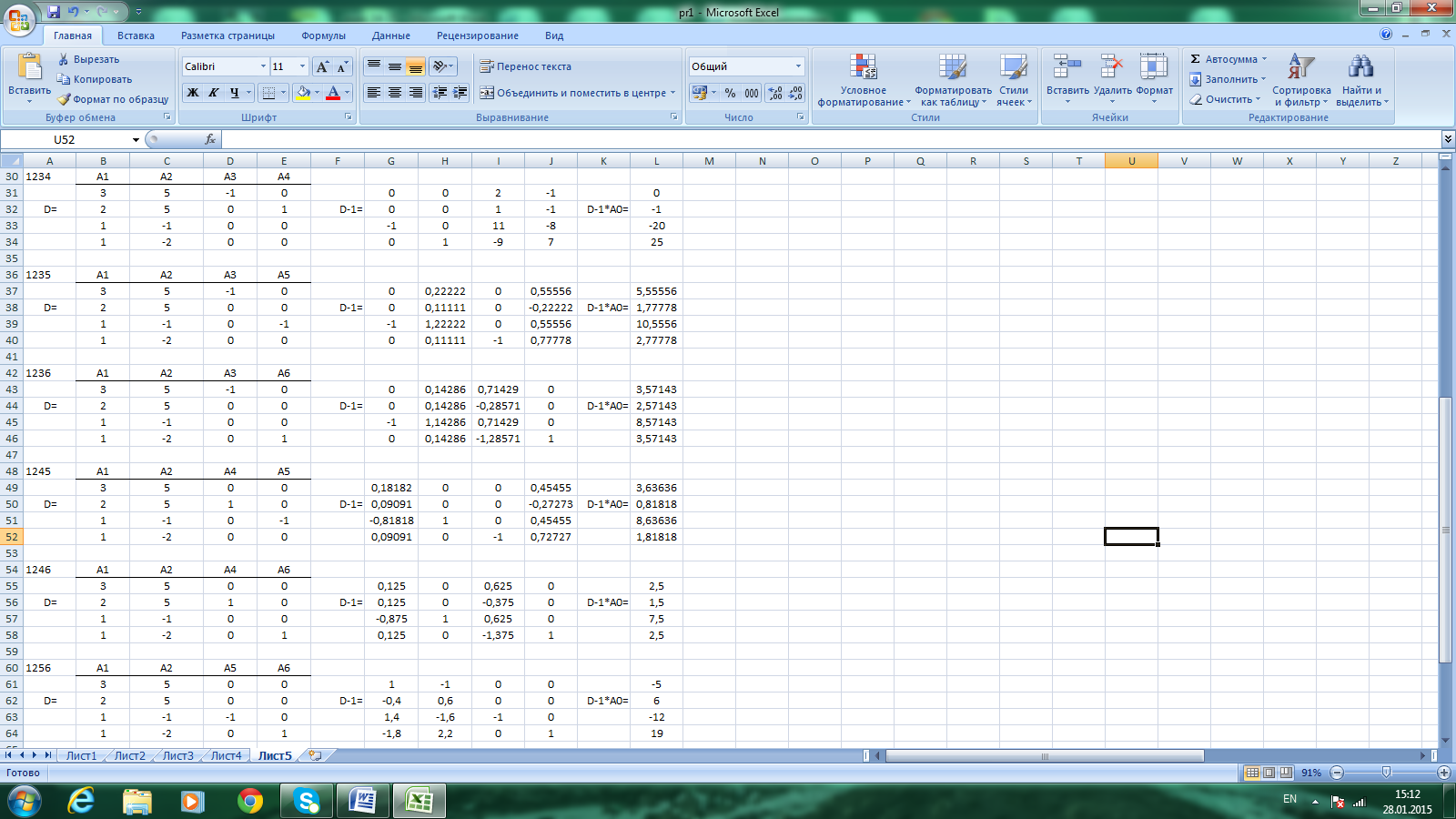

Результат обчислень доцільно об’єднати у таблицю в останньому рядку якої обраховано також значення цільової функції. З шести базисних розв’язків лише чотири – опорні, тобто такі, що не мають від’ємних значень невідомих. Порівняння з результатами попередньої практичної роботи дозволяє зробити важливий теоретичний висновок, що координати вершин багатокутника допустимих значень змінних задачі відповідають опорним розв’язкам еквівалентної системи рівнянь побудованої на обмеженнях задачі.
Результати поточної практичної роботи:
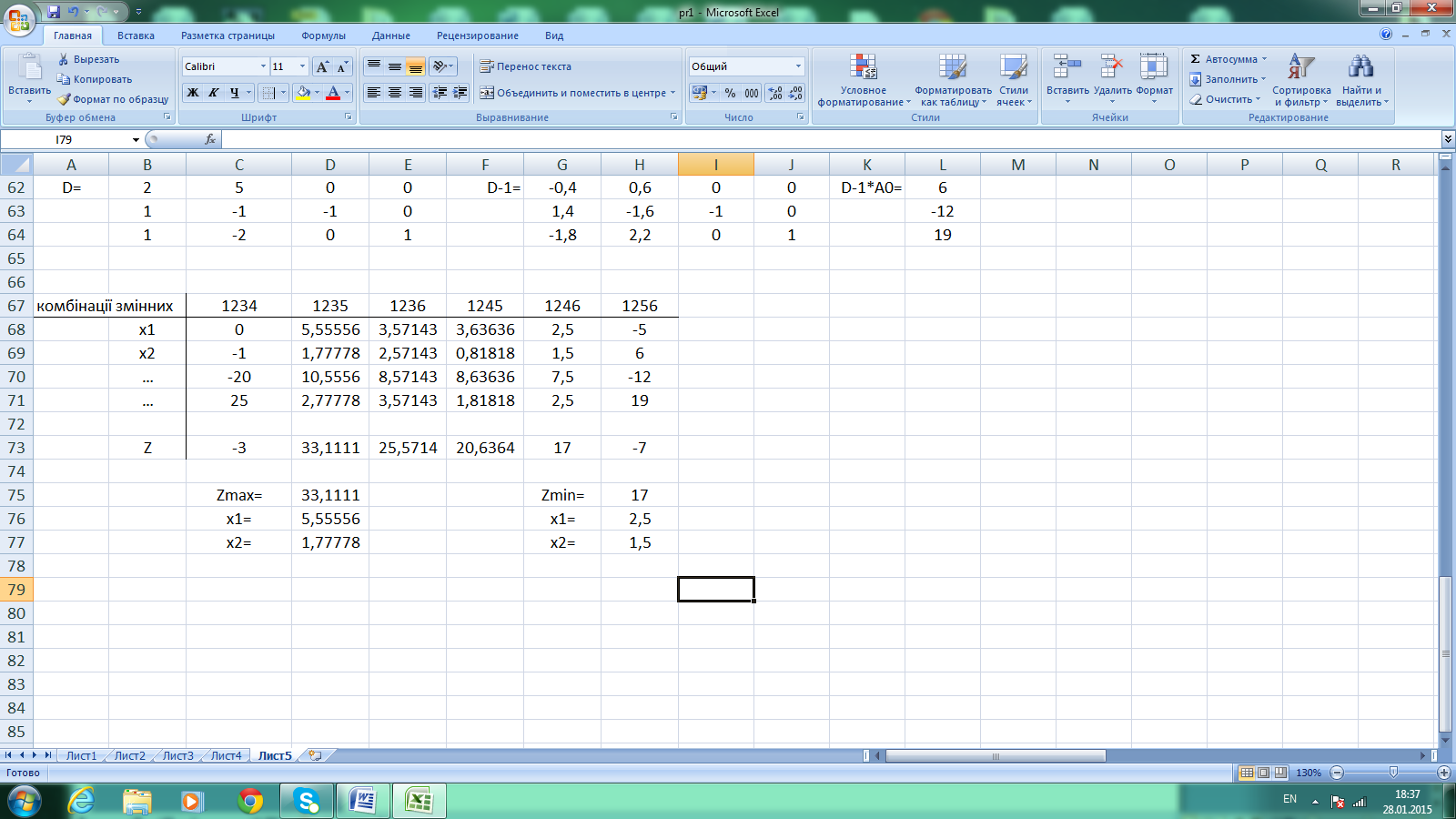
Результати попередньої практичної роботи: