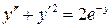Методы интегрирования некоторых классов дифференциальных уравнений, допускающих понижение порядка

Не существует общих приемов, позволяющих проинтегрировать произвольное дифференциальное уравнение высшего порядка. Однако в некоторых случаях порядок дифференциального уравнения может быть понижен и его решение может быть сведено к последовательному интегрированию нескольких дифференциальных уравнений первого порядка. Остановимся на этих случаях.

I. Решение уравнения вида 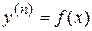сводится к 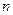кратному интегрированию. Общее решение такого уравнения имеет вид

.

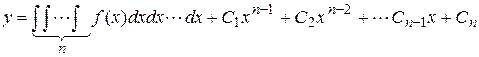Пример.Найти решение уравнения 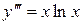, удовлетворяющее условиям

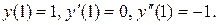(2.3)

Решение. Последовательно интегрируя исходное уравнение, будем иметь

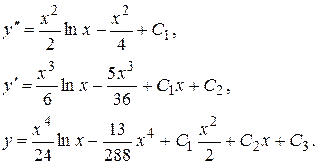
Значения постоянных 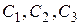найдем из условий (2.3). Для отыскания 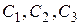получим систему уравнений

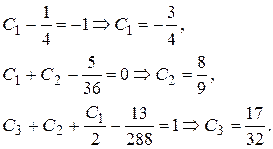
Итак, искомое решение имеет вид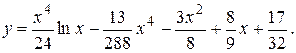

II. Уравнение не содержит 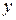и его производных до порядка 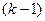включительно, то есть имеет вид .

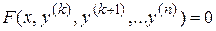Для понижения порядка уравнения применяется подстановка 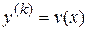. После применения этой подстановки уравнение приобретает вид 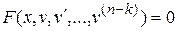. Если удается найти общее решение последнего уравнения 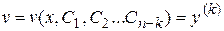, то после 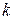-кратного интегрирования получим общее решение исходного уравнения.

Пример.Проинтегрировать уравнение .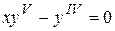

Решение.Уравнение не содержит 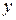и его производных до третьего порядка включительно. Поэтому его порядок понижается путем введения замены 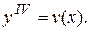Относительно новой переменной уравнение имеет вид

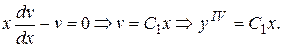
Последовательно интегрируя последнее равенство четыре раза, получим

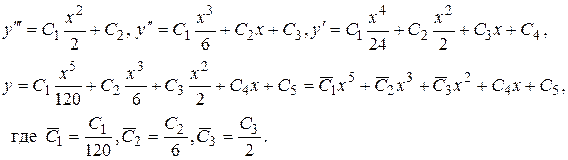
III.Уравнение не содержит явно переменной 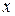, то есть имеет вид 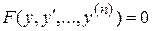. В этом случае порядок уравнения понижается путем замены 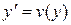. Последовательно получим

.

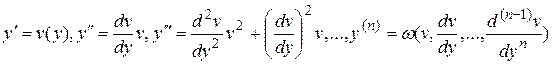Приходим к уравнению 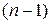-го порядка

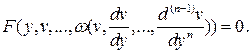
Если удалось найти общее решение последнего уравнения 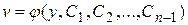, то для отыскания 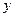будем иметь уравнение с разделяющимися переменными

.

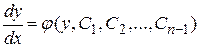Пример.Проинтегрировать уравнение 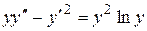в области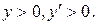

Решение. Уравнение не содержит явно переменной 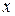. Поэтому выполним замену 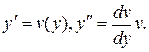Уравнение примет вид 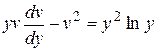. Разделив обе части этого уравнения на 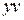, получим 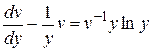– уравнение Бернулли относительно 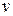. Решение этого уравнения будем искать в виде произведения функций 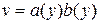. Подставляя в уравнение, будем иметь 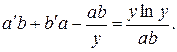В качестве функции 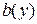возьмем решение уравнения 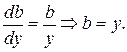Тогда для отыскания 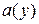получим:

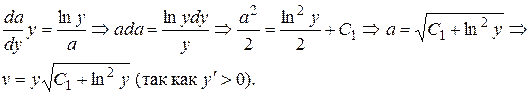
Итак,

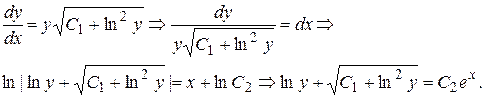
Найден общий интеграл уравнения.

IV. Уравнение однородное относительно 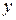и его производных. Однородным называется уравнение , для которого выполнено

.

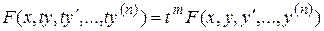Порядок однородного уравнения понижается путем введения новой переменной по правилу 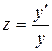. Тогда получим

.

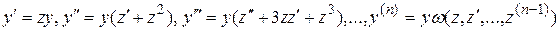При этом исходное уравнение принимает вид

.

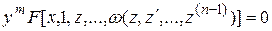Пусть найдено его решение 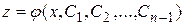. Для нахождения 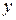получаем уравнение с разделяющимися переменными 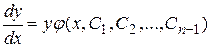, решение которого имеет вид 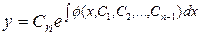. Заметим, что решение 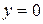здесь не потеряно. Оно получается из последней формулы при .

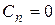Пример.Проинтегрировать уравнение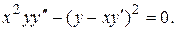

Решение. Левая часть уравнения– однородная функция относительно 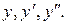Выполним замену 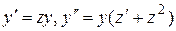. Тогда уравнение примет вид

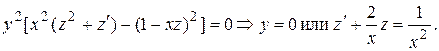
Общее решение последнего уравнения (линейного относительно 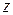) имеет вид 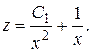Тогда 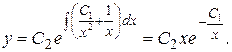Решение 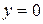получается при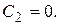

V. Уравнение имеет вид 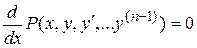. Иными словами, левая часть этого уравнения представляет собой полную производную по 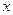от некоторой функции 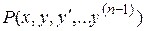. Интегрируя обе части такого уравнения по 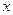, получим новое уравнение, порядок которого на единицу меньше, чем у исходного.

Пример.Проинтегрировать уравнение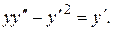

Решение.Очевидным решением этого уравнения является функция 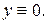Разделив обе части уравнения на 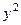, получим

.

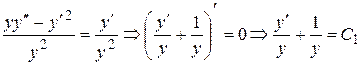При 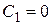получаем 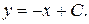При 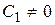получаем линейное уравнение, общее решение которого имеет вид .

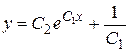Задание 7

Решить дифференциальные уравнения, используя методы понижения порядка. Найти общее или (если заданы начальные условия) частное решение.

1.

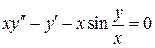
2.

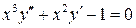
3.

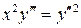
4.

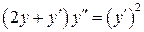
5.

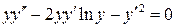
6.

7.

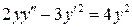
8.

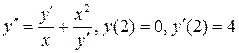
9.

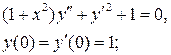
10.

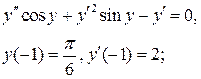
11.

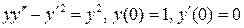
12.

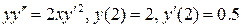
13.

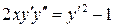
14.

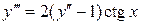
15.

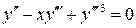
16.

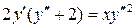
17.

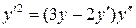
18.

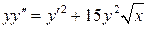
19.

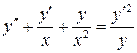
20.

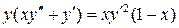
21.

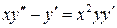
22.

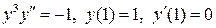
23.

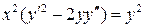
24.

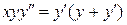
25.

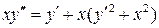
26.

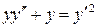
27.

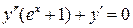
28.

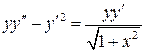
29.

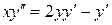
30.

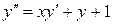
31.