Лекция 38. Основные методы интегрирования. Интегрирование некоторых классов тригонометрических функций

Рассмотрим интегралы от некоторых классов тригонометрических функций. Начнем с наиболее общего случая – интеграла вида

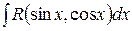, (1)

где под знаком интеграла стоит рациональная функция от тригонометрических аргументов. Этот интеграл с помощью подстановки

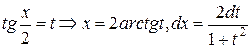(2)

всегда сводится к интегралу от рациональной функции. Выразим sinx и cosx через 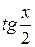, а следовательно, и через t:

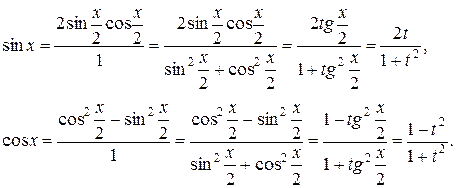(3)

Таким образом, sinx, cosx и dx выразились рационально через t. Так как рациональная функция от рациональных функций есть функция рациональная, то, подставляя полученные выражения в интеграл (1), получим интеграл от рациональной функции:

.

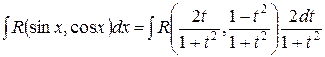Подстановка (2) называется универсальной.

Пример 1. Найти неопределенный интеграл .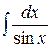

Решение. Выполним универсальную подстановку и на основании формул (2) и (3) имеем:

.

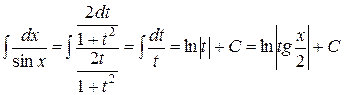Использование универсальной подстановки при интегрировании функций 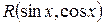часто приводит к громоздким подынтегральным функциям. Поэтому теперь перейдем к рассмотрению частных случаев.

1)Если подынтегральная функция имеет вид 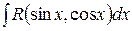, но sinx и cosx входят только в четных степенях ( или если подынтегральная функция обладает свойством четности по двум переменным R(-sinx,-cosx)=R(sinx,cosx) ), то гораздо более рационально применить не универсальную подстановку, а подстановку

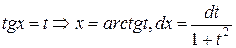(4)

используя эту подстановку и тригонометрические формулы, мы выразим sin² x и cos² x через tgx, а следовательно, через t:

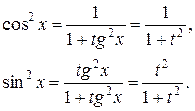(5)

После подстановки мы получим интеграл от рациональной функции

Пример 3. Найти неопределенный интеграл .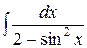

Решение. Выполним подстановку (4) и на основании формул (4) и (5) имеем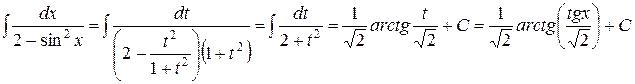

2) Если интеграл имеет вид 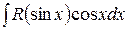(или если подынтегральная функция обладает свойством нечетности по второй переменной R(sinx,-cosx)=-R(sinx,cosx)), то подстановка 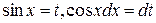приводит этот интеграл к виду .

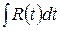3) Если интеграл имеет вид 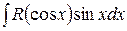(или если подынтегральная функция обладает свойством нечетности по первой переменной R(-sinx,cosx)=-R(sinx,cosx)), то подстановка 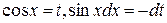приводит этот интеграл к виду .

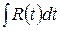4)Если подынтегральная функция зависит только от tgx, то замена tgx=t, x=arctgt, 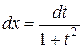приводит этот интеграл к интегралу от рациональной функции .

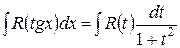Пример 4. Найти неопределенный интеграл .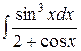

Решение. Этот интеграл легко привести к виду 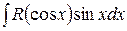. Действительно, 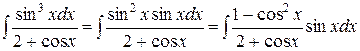. Сделаем замену :

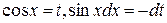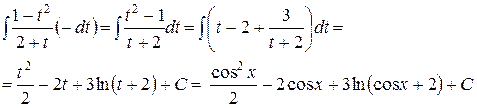
5) Рассмотрим интеграл вида 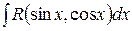с ограничением на подынтегральную функцию – под знаком интеграла стоит произведение 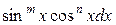( где m и n – целые числа ). Для нас представляют интерес три случая.

а) 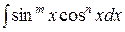, где m и n таковы, что по крайней мере одно из них нечетное число. Допустим для определенности, что n нечетное. Положим n=2p+1 и преобразуем интеграл:

,

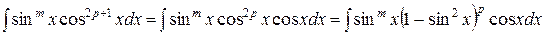сделаем замену переменного: 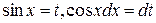. Подставляя новую переменную в данный интеграл, получим

,

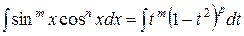а это и есть интеграл от рациональной функции от t.

Пример 5. Найти неопределенный интеграл .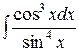

Решение. 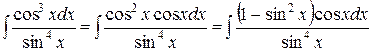. Сделаем замену 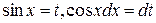, получим:

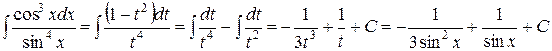
б) 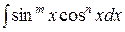, где m и n – числа неотрицательные и четные. Положим m=2p, n=2q. Используем формулы, известные из тригонометрии:

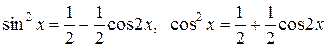. (6)

Подставляя в интеграл, получим:

.

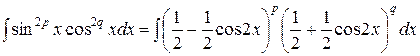Возводя в степень и раскрывая скобки, получим члены, содержащие cos2x в четных и нечетных степенях. Члены с нечетными степенями интегрируются, как указано в пункте а). Четные показатели снова понижаем по формулам (6). Продолжая так, дойдем до членов вида 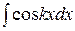, которые легко интегрируются.

Пример 6. Найти неопределенный интеграл .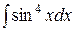

Решение.

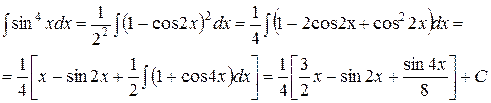
в) Если оба показателя четные, причем хотя бы один из них отрицателен, то предыдущий прием не приводит к цели. Здесь следует сделать замену tgx=t (или ctgx=t )

Пример 7. Найти неопределенный интеграл .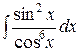

Решение.

.

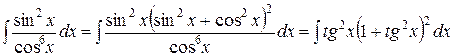Сделаем замену переменного: tgx=t, x=arctgt, 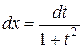, и мы получаем:

.

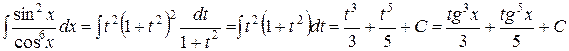6) В заключение рассмотрим интегралы вида:

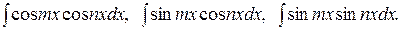
Они легко берутся при помощи следующих тригонометрических формул ( ):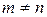

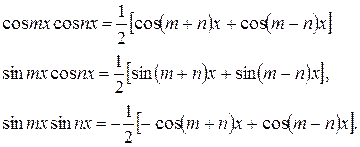
Подставляя и интегрируя, получим:

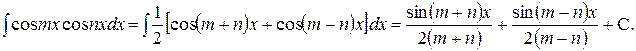
Аналогично вычисляются и два других интеграла.

Пример 8. Найти неопределенный интеграл .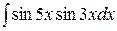

Решение.

.

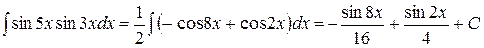Упражнения.

Найти неопределенные интегралы:

1) 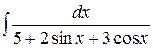. Ответ: .

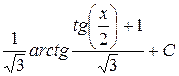2) 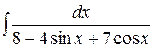. Ответ: .

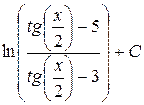3) 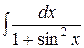. Ответ: .

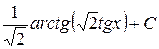4) 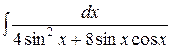. Ответ: .

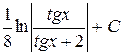5) 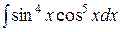. Ответ: .

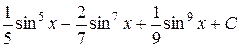6) 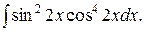Ответ: .

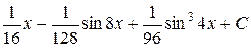7) 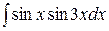. Ответ: .

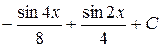8) 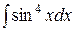. Ответ: .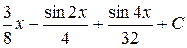