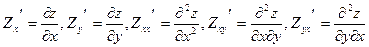Схема исследования функции и исследование её графика
1. Область определения функции, промежутки непрерывности, точки разрыва, вертикальные асимптоты
2. точки пересечения с осями.
3. чётность/нечётность
4. периодичность
5. промежутки монотонности и экстремумы
6. Выпуклости, точки перегиба
7. наклонные асимптоты
Формула Тейлора
Пусть функция y=f(x) определена в некоторой окрестности точки х0 и имеет в этой точке производные (n+1) порядка. Тогда для любого х в (x0-d;x0+d) найдется такое x(кси)Î(х0;х), такая что справедлива формула: 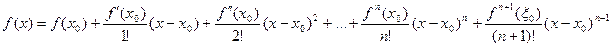
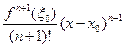 - многочлен Тейлора, остаточный член в формуле Лагранжа.
- многочлен Тейлора, остаточный член в формуле Лагранжа.
Формула Маклорена: называют формулу Тейлора при х0=0.
Функция нескольких переменных.
Предположим, что задано множество D упорядоченных пар чисел. Если каждой паре из множества D по некоторому правилу сопоставить единственную переменную zÎZ, то говорят, что на множестве D задана функция z=f(x;y).
Предел функции двух переменных.
Введём понятие дельта окрестности точки M0(x0;y0). M(x;y)ÎUd(M0), 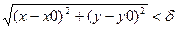 .
.
Определение: пусть функция Z=f(x;y) определена в некоторой окрестности точки М0, за исключением быть может самой точки М0. число А называется пределом функции z=f(x;y) при х®х0, у®у0. M(x;y)®M0(x0,y0).
Если для любого E>0 существует d>0, такое что для всех х¹х0, у¹у0 и удовлетворяет 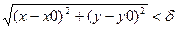 => |f(x,y)-A|<E
=> |f(x,y)-A|<E
Теорема: Пусть функция f(M) и g(M) определены на одном и том же множестве D и имеют следующий предел 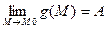 , а
, а 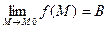 , тогда функции g(M)±f(M); g(M)*f(M); g(M)/f(M), при f(M)¹0, так же имеют пределы, которые соответственно равны A±B, A*B, A/B.
, тогда функции g(M)±f(M); g(M)*f(M); g(M)/f(M), при f(M)¹0, так же имеют пределы, которые соответственно равны A±B, A*B, A/B.
Функция z=f(M) называется бесконечно малой при M®M0. Если 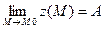 , то тогда функция может быть представлена в виде: Z(M)=A+a(M)
, то тогда функция может быть представлена в виде: Z(M)=A+a(M)
Непрерывность функции 2-х переменных
Определение: Пусть функция определена в некоторой окрестности точки М0. функция f(M) называется непрерывной в точке М0, если существует предел функции в этой точке и он равен значению функции в этой точке 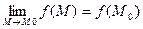
Определение: функция, непрерывная в каждой точке некоторой области называется непрерывной на всей этой области.
Определение: Точки в которых нарушается непрерывность называются точками разрыва.
Функция, z=f(x,y) называется непрерывной в точке М0, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Частные производные
Рассмотрим функцию z=f(M) в некоторой окрестности точки М, придадим переменной х в М некоторое приращение, зафиксировав при этом у. От точки М перейдём к точке М1: М(x;у)®М1(х+Dх;у), тогда соответствующее приращение функции DxZ=∫f( х+Dх;у)-f(x;y) называется частным приращением по х в точке М.
Если существует 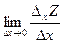 , то говорят о том, что существует частная производная
, то говорят о том, что существует частная производная 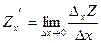 , соответственно частная производная по y:
, соответственно частная производная по y: 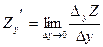 .
.
Если Zx’ определена в окрестности точки М и существует производная этой функции по переменной х, то это производная второго порядка. 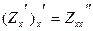
Если существует частная производная по у, то её называют смешанной производной второго порядка. 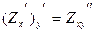
Теорема: Если существуют смешанные производные второго порядка Zxy’’ и Zyx’’, в некоторой окрестности точки М, и непрерывны в самой точке М, то они равны между собой в этой точке.
Замечание: