Метод Гаусса решения линейных систем

Замечание. Линейная система (2.2) может иметь единственное решение, бесконечно много решений или не иметь ни одного решения.

Примеры:

1. 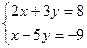. Единственным решением является пара чисел х = 1, у = 2.

2. 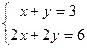. Решением этой системы будут любые два числа х и у, удовлетворяющие условию у = 3 – х. Например, х=1, у=2; х=0, у=3 и т. д.

3. 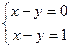. Очевидно, что эта система не имеет решений, так как разность двух чисел не может принимать двух различных значений.

Условия существования и количества решений линейной системы будут изучены в дальнейшем, а пока рассмотрим способы нахождения единственного решения системы,

в которой число уравнений равно числу неизвестных: 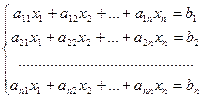(2.3)

Пусть 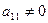(этого всегда можно добиться, поменяв уравнения местами). Разделим обе части первого уравнения на 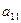и вычтем полученное уравнение из каждого из остальных уравнений системы, умножив его предварительно на 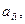где i – номер очередного уравнения. Как известно, полученная при этом новая система будет равносильна исходной. Коэффициенты при 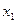во всех уравнениях этой системы, начиная со второго, будут равны 0, т.е. система выглядит так:

.

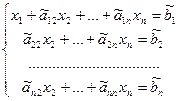Если новые коэффициенты при х₂ не все равны нулю, можнотаким же образом исключить 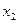из третьего и последующих уравнений. Продолжая эту операцию для следующих неизвестных, приведем систему к так называемому треугольному виду:

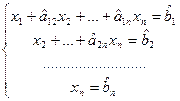. (2.4)

Здесь символам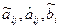и и 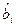обозначены изменившиеся в результате преобразований числовые коэффициенты и свободные члены.

Из последнего уравнения системы (2.4) единственным образом определяется 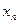, а затем последовательной подстановкой – остальные неизвестные.

Замечание. Иногда в результате преобразований в каком-либо из уравнений обращаются в 0 все коэффициенты и правая часть, то есть оно превращается в тождество 0=0. Исключив его из системы, мы уменьшим число уравнений по сравнению с числом неизвестных. Такая система не может иметь единственного решения.

Если же в процессе применения метода Гаусса какое-нибудь уравнение превратится в равенство вида 0=1 (коэффициенты при неизвестных обратились в 0, а правая часть приняла ненулевое значение), то исходная система не имеет решения, так как подобное равенство является неверным при любых значениях неизвестных.

Примеры:

1. Решим методом Гаусса систему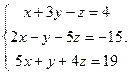

Вычтем из второго уравнения удвоенное первое, а из третьего – первое, умноженное на 5.

Получим: 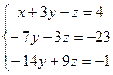. Теперь вычтем из третьего уравнения удвоенное второе, а затем разделим второе уравнение на –7 (коэффициент при у), а третье – на 15 (новый коэффициент при z). Система примет вид:

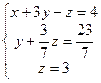. Отсюда z=3, y=2, x=1 – единственное решение системы.

2. Система 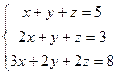после исключения х из второго и третьего уравнений примет вид: 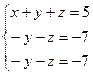. Если затем вычесть второе уравнение из третьего, то последнее уравнение станет тождеством 0=0. В системе осталось два уравнения: 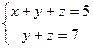. Ее решение можно записать в виде: х = -2, у – любое число, z = 7 – y. Таким образом, система имеет бесконечно много решений.

3. 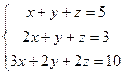. Применив к этой системе метод Гаусса, получим ,

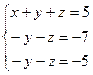откуда 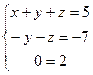. Последнее равенство является неверным при любых значениях неизвестных, следовательно, система не имеет решения.

Правило Крамера.

Рассмотрим систему (2.3). Назовем главным определителем этой системы определитель 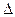, элементами которого являются коэффициенты при неизвестных:

.

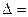
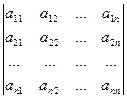Предположим сначала, что 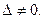Умножим каждое уравнение системы (2.3) на алгебраические дополнения 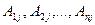элементов j-го столбца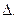

Сложив затем все уравнения, получим:

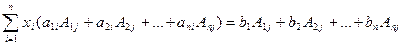. (2.5)

Отметим, что .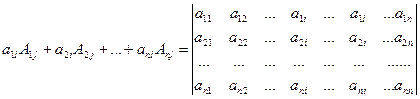

(j-й столбец)

(Результат получен из разложения определителя по j-му столбцу). Такой определитель равен 0 при 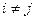и равен 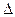при i = j. Правая часть равенства (2.5) представляет собой определитель 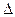, в котором вместо j-го столбца стоит столбец свободных членов системы (2.3). Назовем такой определитель 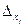. Рассматривая j = 1,2,…,n, получим систему, эквивалентную исходной: 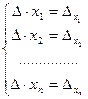(2.6) . Разделив все уравнения на 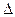, найдем единственное решение: .

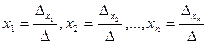Предположим теперь, что 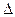=0. Тогда система (2.6) примет вид: .

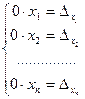В этом случае, если все 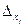=0, система выглядит так: 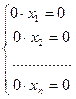и имеет бесконечно много решений. Если же хотя бы один из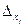 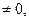система решений не имеет.

Таким образом, правило Крамера позволяет найти единственное решение системы (2.3) или сделать вывод о существовании бесконечного числа решений либо об их отсутствии:

1) Если 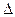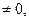система (2.3) имеет единственное решение, определяемое по формулам: .

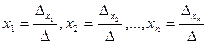2) Если 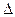= =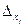0, система имеет бесконечно много решений.

3) Если 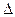=0, а хотя бы один из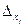 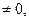система не имеет решений.

Примеры:

1. Рассмотрим систему 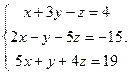, решенную в предыдущем разделе методом Гаусса, и применим к ней правило Крамера. Найдем все нужные определители:

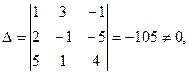следовательно, система имеет единственное решение.

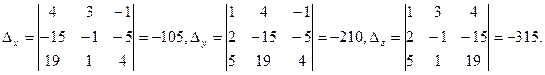
Отсюда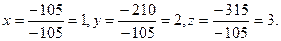

2. 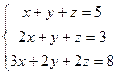. Здесь 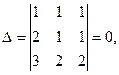поскольку имеет два одинаковых столбца.

Следовательно, система не имеет единственного решения. Найдем 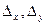и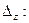

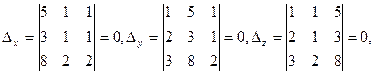поэтому система имеет бесконечно много решений.

3. 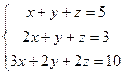. Для этой системы 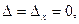но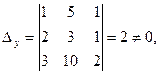

следовательно, решений нет.