Метод Гаусса решения линейных систем
Метод Гаусса для невырожденных квадратных линейных систем (3.1) состоит в том, что
1) с помощью элементарных преобразований:
а) перестановки любых двух уравнений местами;
б) прибавление к любому уравнению другого уравнения, умноженного на число
система приводится к равносильной системе
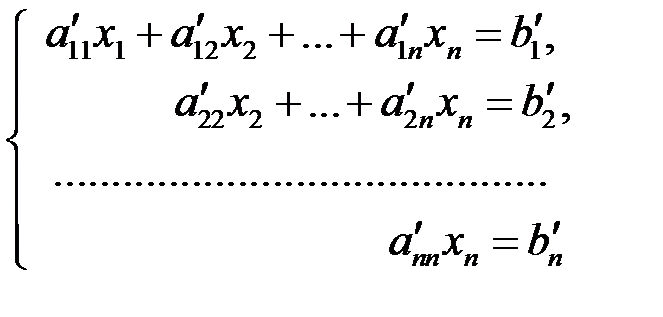 (3.4)
(3.4)
с треугольной основной матрицей, имеющей тот же определитель, что и матрица 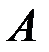 , а потому с ненулевыми диагональными элементами
, а потому с ненулевыми диагональными элементами 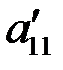 ,
, 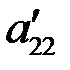 , …,
, …, 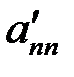 (прямой ход метода);
(прямой ход метода);
2) из системы (3.4) последовательно находятся значения неизвестных, начиная с последнего (обратный ход метода):
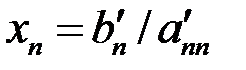 ,…,
,…,  ,
,  .
.
Заметим, что невырожденность квадратной линейной системы, то есть условие 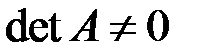 , до начала решения проверять не нужно; если система приводится к виду (3.4), то она невырожденная.
, до начала решения проверять не нужно; если система приводится к виду (3.4), то она невырожденная.
Метод Гаусса можно распространить на любую линейную систему (3.1), добавив к числу элементарных преобразований
в) перенумерацию неизвестных;
г) удаление «нулевого уравнения» 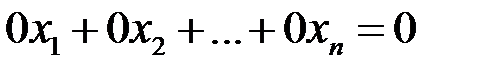 , которому удовлетворяет любой набор чисел
, которому удовлетворяет любой набор чисел 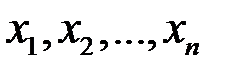 .
.
Если по ходу преобразований встретится уравнение вида 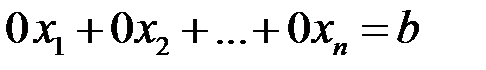 , где
, где 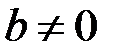 , то оно не имеет решений и, тем более, вся система не имеет решений – несовместна.
, то оно не имеет решений и, тем более, вся система не имеет решений – несовместна.
Если такое уравнение не встретилось, то система преобразуется в равносильную систему из 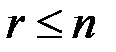 уравнений
уравнений
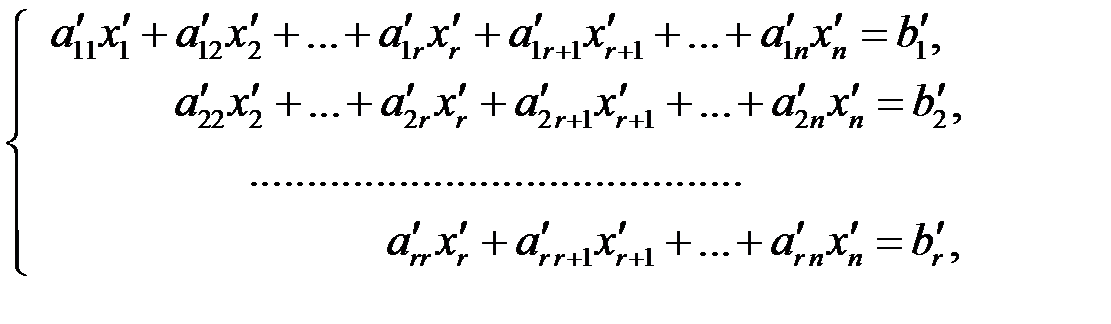 (3.5)
(3.5)
где 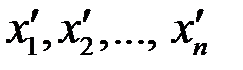 все те же неизвестные
все те же неизвестные 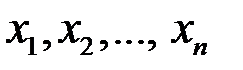 , но возможно пронумерованные в другом порядке, а числа
, но возможно пронумерованные в другом порядке, а числа 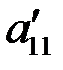 ,
, 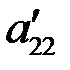 ,…,
,…, 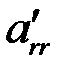 не равны нулю.
не равны нулю.
Если 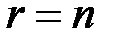 , то, как и выше, обратным ходом получаем единственное решение. Система определенна.
, то, как и выше, обратным ходом получаем единственное решение. Система определенна.
Если 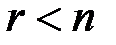 , то неизвестным
, то неизвестным 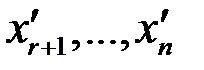 придаем произвольные значения
придаем произвольные значения 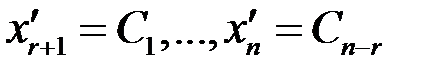 и из (3.5) обратным ходом выражаем последовательно
и из (3.5) обратным ходом выражаем последовательно 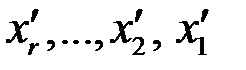 через
через 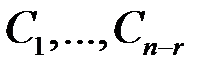 . В итоге имеем бесконечное множество решений, зависящих от
. В итоге имеем бесконечное множество решений, зависящих от 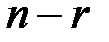 произвольных постоянных
произвольных постоянных 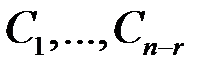 , меняя которые получим все решения. Таким образом, в этом случае система неопределенна.
, меняя которые получим все решения. Таким образом, в этом случае система неопределенна.
Примеры решения задач
3.2.1.Решить линейную систему
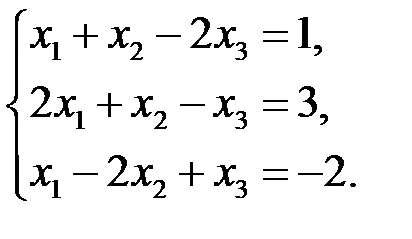 (3.6)
(3.6)
Решение 1 (По формулам Крамера).
◄ Линейная система (3.6) – квадратная: число уравнений равно числу неизвестных – трем. Определитель основной матрицы (из коэффициентов при неизвестных)
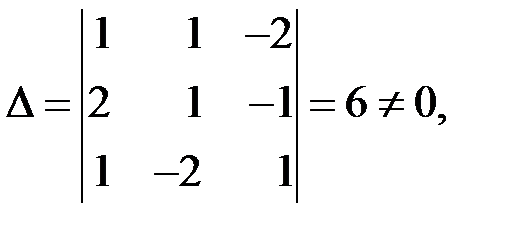
то есть система невырожденная, и можно применять формулы Крамера (3.3). Составим и вычислим определители 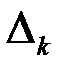 ,
, 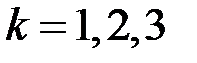 , заменив в
, заменив в 
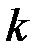 -й столбец на столбец свободных членов:
-й столбец на столбец свободных членов:
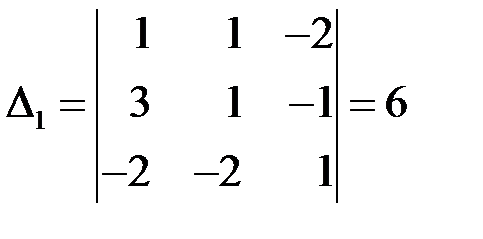 ,
, 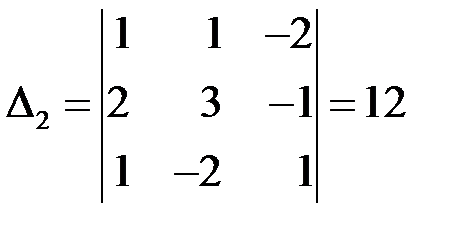 ,
, 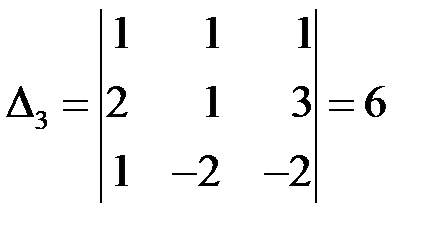 .
.
По формулам Крамера (3.3) 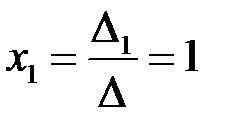 ,
, 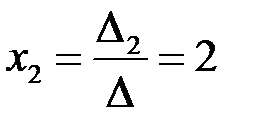 ,
, 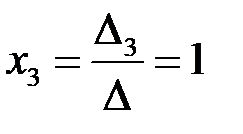 .►
.►
Решение 2 (Матричным методом – с помощью обратной матрицы).
◄ Линейную систему (3.6) можно записать в виде одного матричного уравнения 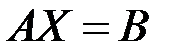 , где
, где 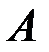 – основная матрица системы,
– основная матрица системы, 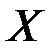 – матрица-столбец из неизвестных
– матрица-столбец из неизвестных 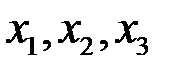 ,
, 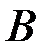 – матрица-столбец из свободных членов. Матрица, обратная к
– матрица-столбец из свободных членов. Матрица, обратная к 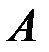 , была вычислена в примере 2.2.5. Решение системы находим по формуле (3.2):
, была вычислена в примере 2.2.5. Решение системы находим по формуле (3.2):
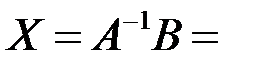
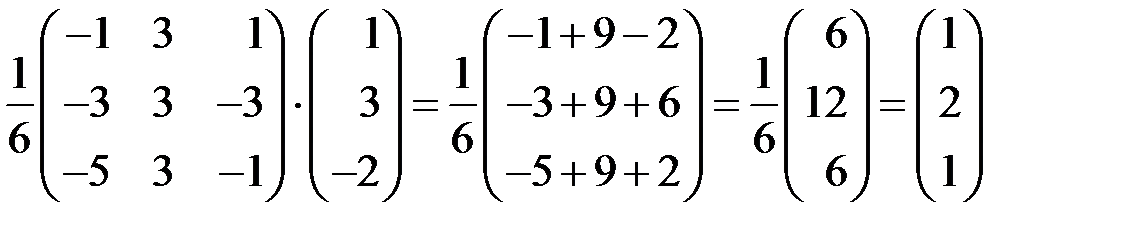 ,
,
то есть 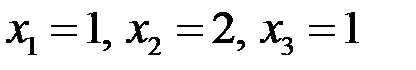 .►
.►
Решение 3 (Методом Гаусса).
◄ Прямой ход метода:
Шаг 1. Ко второму уравнению прибавляем первое, умноженное на ( 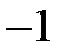 ), к третьему прибавляем первое, умноженное на (
), к третьему прибавляем первое, умноженное на ( 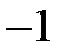 ).
).
Шаг 2. К третьему уравнению прибавляем первое, умноженное на ( 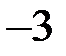 ).
).
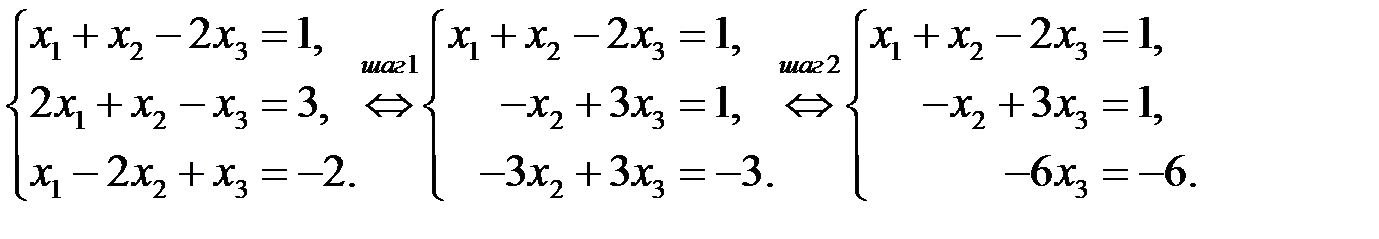
Обратный ход метода: Начиная с последнего уравнения, последовательно находим 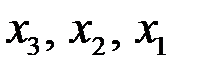 :
:
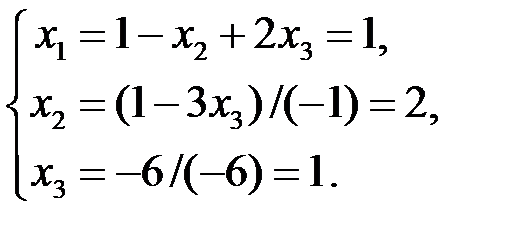
Замечание. Разумно упростить процедуру, выписывая только матрицу из коэффициентов при неизвестных и свободных членов (расширенную матрицу системы):
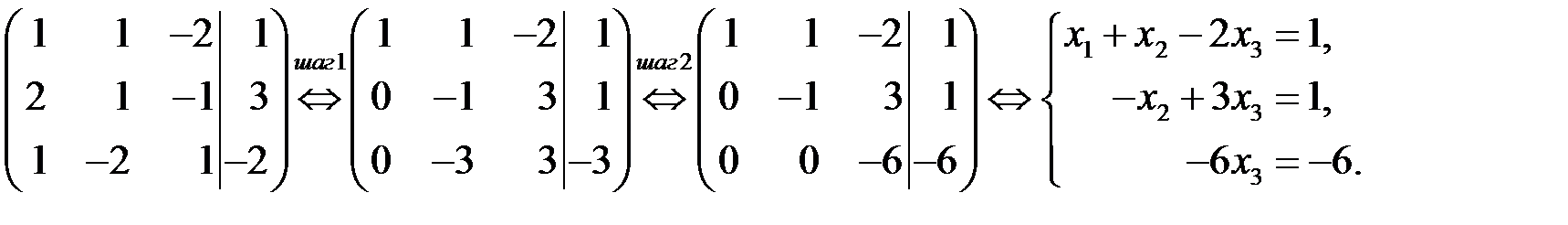
На последнем шаге прямого хода мы для наглядности все-таки вернулись к подробной записи системы. ►
3.2.2.Решить линейную систему 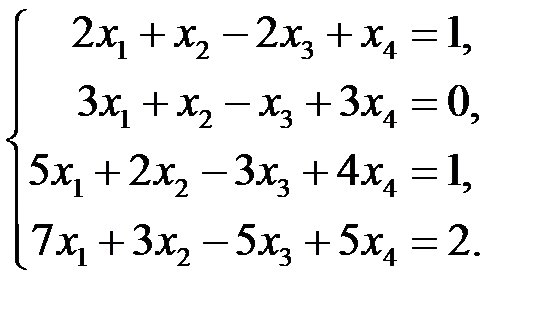
◄ Решаем методом Гаусса. Прямой ход метода:
Шаг 1. Первое уравнение заменим на разность между вторым и первым. Цель – получить 1 в качестве коэффициента при 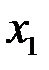 в первом уравнении.
в первом уравнении.
Шаг 2 . Ко второму уравнению прибавляем первое, умноженное на (–3), к третьему прибавляем первое, умноженное на (–5), к четвертому прибавляем первое, умноженное на (–7).
Шаг 3. К третьему уравнению прибавляем второе, умноженное на ( 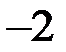 ), к четвертому прибавляем второе, умноженное на (–3).
), к четвертому прибавляем второе, умноженное на (–3).
Шаг 4. Отбрасываем нулевые уравнения.
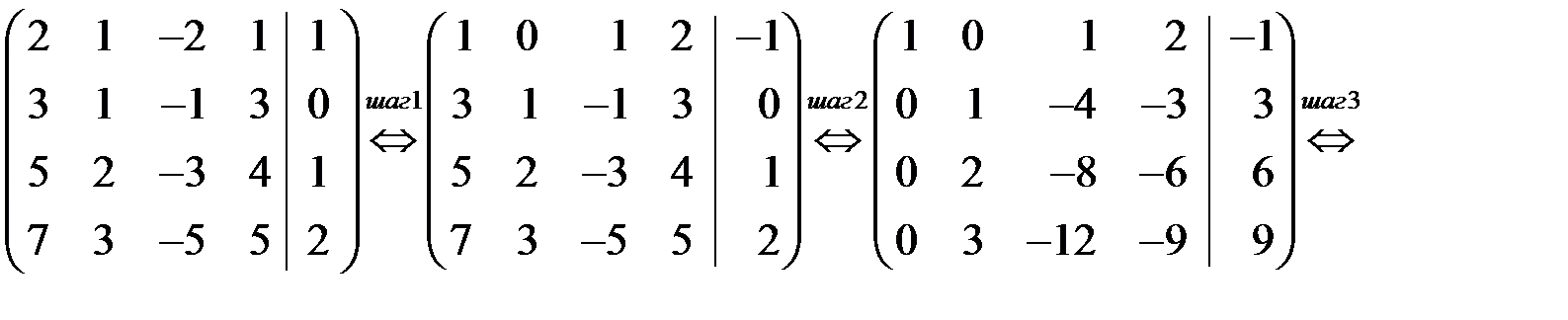
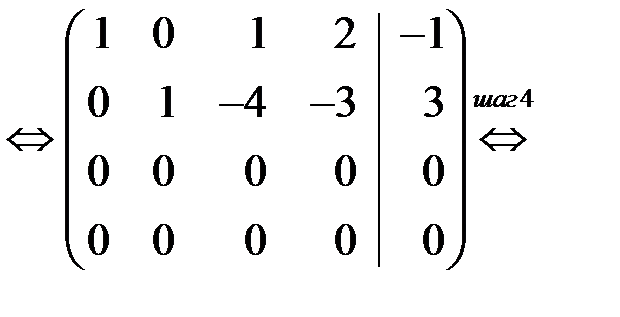
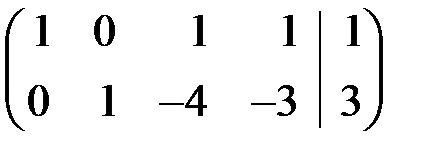

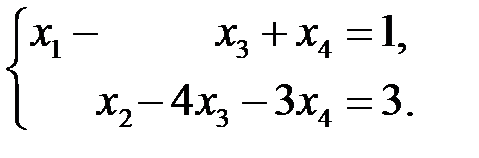
Обратный ход метода: Неизвестным 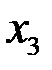 и
и 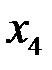 можно придать произвольные значения:
можно придать произвольные значения: 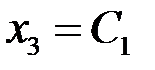 ,
, 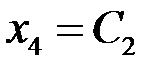 . Тогда
. Тогда
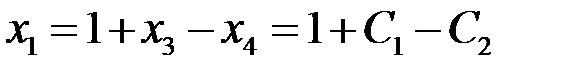 ,
, 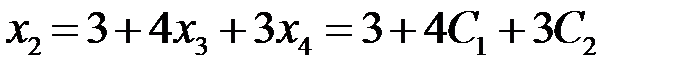 .
.
Таким образом, все решения (общее решение) системы задаются формулами 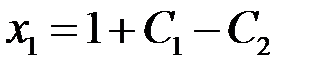 ,
, 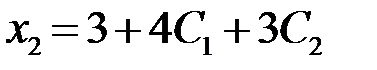 ,
, 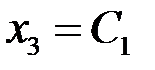 ,
, 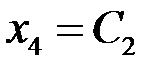 , где
, где 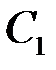 и
и 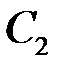 – произвольные числа. Меняя
– произвольные числа. Меняя 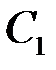 и
и 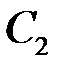 , мы получим любое решение. ►
, мы получим любое решение. ►
