Метод Гаусса решения систем линейных уравнений
Рассмотрим квадратную систему
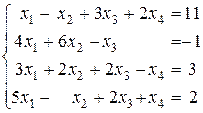. (1.1.9)
У этой системы коэффициент a11 отличен от нуля. Если бы это условие не выполнялось, то чтобы его получить, нужно было бы переставить местами уравнения, поставив первым то уравнение, у которого коэффициент при x1 не равен нулю.
Проведем следующие преобразования системы:
1) поскольку a11¹0, первое уравнение оставим без изменений;
2) вместо второго уравнения запишем уравнение, получающееся, если из второго уравнения вычесть первое, умноженное на 4;
3) вместо третьего уравнения запишем разность третьего и первого, умноженного на 3;
4) вместо четвертого уравнения запишем разность четвертого и первого, умноженного на 5.
Полученная новая система эквивалентна исходной и имеет во всех уравнениях, кроме первого, нулевые коэффициенты при x1 (это и являлось целью преобразований 1 – 4):
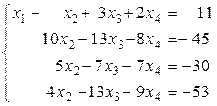. (1.1.10)
Можно доказать, что замена любого уравнения системы новым, получающимся прибавлением к данному уравнению любого другого уравнения системы, умноженного на любое число, является эквивалентным преобразованием системы.
Для приведенного преобразования и для всех дальнейших преобразований не следует целиком переписывать всю систему, как это только что сделано. Исходную систему можно представить в виде матрицы
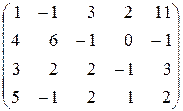. (1.1.11)
Матрица (1.1.11) называется расширенной матрицей для исходной системы уравнений. Если из расширенной матрицы удалить столбец свободных членов, то получится матрица коэффициентов системы, которую иногда называют просто матрицей системы.
Каждую систему m линейных уравнений с n неизвестными можно представить в виде расширенной матрицы, содержащей m строк и n+1 столбцов. Каждую матрицу можно считать расширенной матрицей или матрицей коэффициентов некоторой системы линейных уравнений. Системе (1.1.10) соответствует расширенная матрица
.
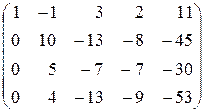Преобразуем эту матрицу следующим образом:
1) первые две строки оставим без изменения, поскольку элемент a22 не равен нулю;
2) вместо третьей строки запишем разность между второй строкой и удвоенной третьей;
3) четвертую строку заменим разностью между удвоенной второй строкой и умноженной на 5 четвертой.
В результате получится матрица, соответствующая системе, у которой неизвестная x1 исключена из всех уравнений, кроме первого, а неизвестная x2 — из всех уравнений кроме первого и второго:
.
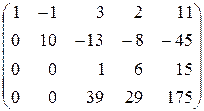Теперь исключим неизвестную x3 из четвертого уравнения. Для этого последнюю матрицу преобразуем так:
1) первые три строки оставим без изменения, так как a33 ¹ 0;
2) четвертую строку заменим разностью между третьей, умноженной на 39, и четвертой:
.
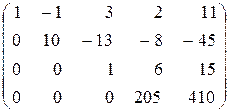Полученная матрица соответствует системе
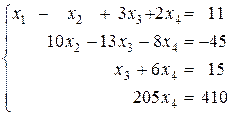. (1.1.12)
Из последнего уравнения этой системы получаем x4 = 2. Подставив это значение в третье уравнение, получим x3 = 3. Теперь из второго уравнения следует, что x2 = 1, а из первого — x1 = –1. Очевидно, что полученное решение единственно (так как единственным образом определяется значение x4, затем x3 и т. д.).
Назовем элементарными преобразованиями матрицы следующие преобразования:
1) перемена местами двух строк;
2) умножение строки на число, отличное от нуля;
3) замена строки матрицы суммой этой строки с любой другой строкой, умноженной на некоторое число.
Если матрица A является расширенной матрицей некоторой системы, и путем ряда элементарных преобразований матрицаAпереводится в матрицу B, являющуюся расширенной матрицей некоторой другой системы, то эти системы эквивалентны.
Назовем квадратную матрицу, у которой на главной диагонали стоят числа, отличные от нуля, а под главной диагональю – нули, треугольной матрицей. Матрица коэффициентов системы (1.1.12) – треугольная матрица.
Если с помощью элементарных преобразований матрицу коэффициентов квадратной системы можно привести к треугольной матрице, то система совместна и определенна.
Пример 1.1.11. Решить систему
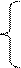x1+7x2+3x3+2x4=6
2x1+5x2+2x3+3x4=4
7x1+4x2+x3+9x4=2
В этой системеm=3 - количество уравнений; n=4 -количество неизвестных.
Запишем расширенную матрицу системы А и преобразуем ее к ступенчатому виду
_
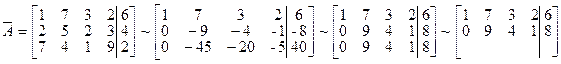
RgA=2, rgA=2. По теореме Кронекера-Капелли СЛАУ совместна. Укороченная СЛАУ имеет вид:
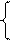x1+7x2+3x3+2x4=6
9x2+4x3+x4=8
В качестве базисных неизвестных выберем неизвестные х1 и x2, а неизвестные, x3, x4 примем за свободные, полагая x3=C1, x4=C2. Тогда СЛАУ может быть записана в виде
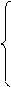x1+7x2=6-3C1-2C2
9x2=8-4C1-C2
x3=C1
x4=C2
Откуда находим
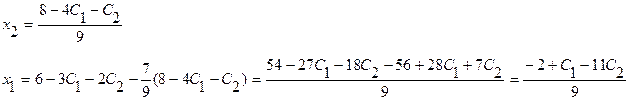
или окончательно получим
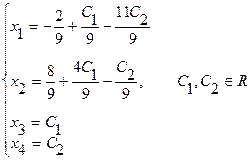
Пример 1.1.12. Решить систему
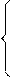x1+2x2-3x3+x4=-4
2x1-x2+x3-x4=2
-x1+3x2-x3+3x4=0
2x1+4x2-3x3 +2x4=3
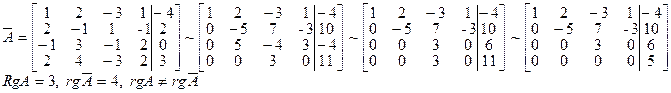
Система линейных алгебраических уравнений несовместна.
Замечание. Однородные СЛАУ всегда совместны, т.к. ранги расширенной матрицы системы и матрицы системы совпадают.
Вопросы для самопроверки
1. Какие матрицы называются равными?
2. В каких случаях возможно перемножение двух матриц?
3. В каких случаях существуют произведения как АВ так и ВА?
4. Что называется минором и алгебраическим дополнением элементов матрицы? В чем отличие между ними?
5. Сформулируйте правило Крамера.
6. Как осуществляется транспонирование матрицы?
7. В чем суть метода элементарных преобразований получения обратной матрицы?
8. Что такое ранг матрицы?
9. Что такое основная и расширенная матрицы системы?
10. Сформулируйте и поясните на примерах теорему Кронекера-Капелли.