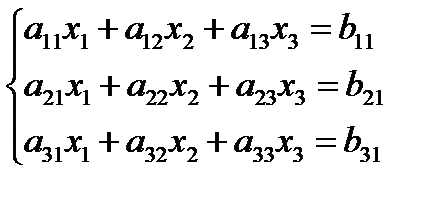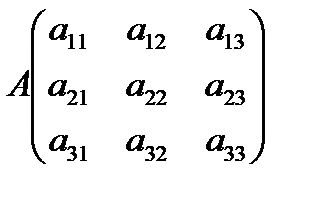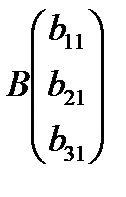Билет 11. Метод Гаусса решения систем линейных уравнений.

Билет 1

Множества - совокупность некоторых объектов объединённых по какому-либо признаку.

Операции с множествами: объединение, пересечение, относительное дополнение от А до В, симметричная разность, абсолютное дополнение

Объединение множеств - множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств AUB

Пересечение множеств – множество, состоящее из элементов, каждый из которых принадлежит множеству А или множеству В

Относительное дополнение от А до В

Симметричная разность А+В=(А\В)U(B\A)

Абсолютное дополнение A=V\A

Билет 2

Вещественные (действительные) числа – множество всех бесконечных десятичных дробей

Свойства

a+b=b+a a=b,b=c => a=c

(a+b)+c=a+ (b+c) a>b,b>c => a>c, a>b => a+c>b+c, a>0,b>0 => ab>0

ab=ba Непрерывность вещ.чисел a>b => -a<-b

(ab)c=a(bc) a>b => a-b>0

(a+b)c=ac+bc a+(-b)+(-a)>0+(-a)

0+a=a a+(-a)+(-b)>-a

a+(-a)=0 0+(-b)>-a

1*a=a -b>-a

a не равно 0 => a*a(в -1 степени)=1

Билет 3

Абсолютная величина числа – расстояние от числа до нуля

Свойства

Модуль х больше либо равен 0

Модуль х равен модулю -х

Модуль х со знаком – за модулем меньше либо равно х или меньше либо равно модулю х

Теорема 1

Теорема 2

Билет 4

- существует, - для любого

1^2+2^2+3^2+…+n^2=n(n+1)(2n+1)/6 n

1) n=1 1^2=1(1+1)(2+1)/6=1

2) n => n+1

Билет 5

Определитель – число detА квадратной матрицы А порядка n

а(11) a(12) … a(1n)

a(21) a(22) … a(2n)

a(n1) a(n2) … a(nn)

Свойства

1.Значение определителя не изменится от замены строк столбцами

2.Определитель с двумя одинаковыми рядами равен нулю

3.Если все элементы какого-нибудь ряда умножить на одно то же число, то значение определителя умножится на это же число

4.Если все элементы какого-нибудь ряда обладают общим множителем, то этот множитель можно вынести за знак определителя

5.Определитель с двумя пропорциональными рядами равен нулю

6.Если элементы какого-либо ряда определителя представляет собой сумму двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей

7.

8.Если в определители поменять местами два ряда, то он изменит знак, а по модулю не изменит

Билет 6

Минор элемента а- определитель, который получается из первоначального путём вычёркивания строки и столбца проходящих через данный элемент

Алгебраическим дополнением А а- (-1)^i+j М

Теорема 1: Если в определители порядка n все элементы строчки i (или столбца) равны 0, кроме элемента а, то значение определителя равно А а

Теорема 2: Какую бы строчку или столбец определителя порядка n мы не взяли, значение определителя равно сумме произведений элементов этой строки или столбца на их алгебраическое дополнение

Билет 7

Матрица- прямоугольная таблица чисел, содержащая m строк одинаковой длины или n столбцов одинаковой длины

Действия с матрицами:

Сложение

2 -1 4 1 1 -3 3 0 -1

3 0 8 0 11 2 3 11 10

Умножение на число

2А+5В= 16 25

13 -8

А= 3 5 В= 2 3 2А= 6 10 5В= 10 15

4 1 -1 2 8 -2 -5 10

Произведение

А= 1 3 2 В= 1 3 6 1

1 6 4 2 3 4 1

2 5 1 3

С(11)=1*1+3*2+2*2=11

С(12)=1*3+3*3+2*5)=22 С= 11 22 20 10

С(13)=1*6+3*4+2*1=20 21 41 34 19

С(14)=1*1+3*1+2*3=10

С(21)=1*1+6*2+4*2=21

С(22)=1*3+6*3+4*5=41

С(23)=6*1+6*4+4*1=34

С(24)=1*1+6*1+4*3=19

Билет 8

Транспортирование- поворот вокруг главной диагонали

А= a(11) a(12) … a(1n) A^T= a(11) a(21) a(m1)

a(21) a(22) … a(2n) a(21) a(22) a(m2)

a(m1) a(m2) … a(mn) a(1n) a(2n) a(mn)

Свойства

1.(А+В)^T=A^T+B^T

2.(A*B)^T=A^T*B^T

Обратная матрица – всякая невырожденная матрица. Существует только для квадратной

А= a(11) a(12) … a(13) A^*= a(11) a(21) a(31)

a(21) a(22) … a(23) a(12) a(22) a(32)

a(31) a(32) … a(33) a(13) a(23) a(33)

Свойства

1.A^-1*A=A*A^-1=E (обратная матрица)

2.A^-1=1/detA (A^*)^t (квадратная матрица)

Теорема: Если для матрицы существует обратная матрица, то она единственная

Билет 9

Ранг матрицы - наибольший из порядков миноров данной матрицы, отличных от нуля. Обозначается r(A)

Свойства ранга матрицы

1.при транспортировании матрицы её ранг не меняется

2.если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится

3.ранг матрицы не изменяется при элементарных преобразованиях матрицы

Элементарные преобразования матрицы

1.перестановка строк

2.умножение элементов какой-нибудь строки на ненулевое число

3.прибавление к элементам одной строки элементов другой строки умножается на одно и то же число

Ступенчатая матрица- матрица, где каждая строка имеет хотя бы один ненулевой элемент, если ненулевой элемент каждой строки, начиная со второй, расположен правее ненулевого элемента предыдущей строки

Теорема: Любую матрицу A с помощью элементарных преобразований можно преобразовать в ступенчатую матрицу

Билет 10

Для того, чтобы система однородных линейных уравнений имела нетревиальное решение, необходимо чтобы ранг её основной матрицы А был меньше числа неивестного
1.Несовместные линейные уравнения- не имеют решения.
2.Совместные-решение есть
А)Определённые- одно решение
Б)Неопределённые- решений бесконечно много

Метод Крамера
Xj=Дельтаj/дельта, j=1,2,3

Матричный метод

X=A^-1*B

Метод Гаусса.

Сначала следует привести систему к треугольному (ступенчатому) виду, а затем ступенчато решить.

Формула Крамера.

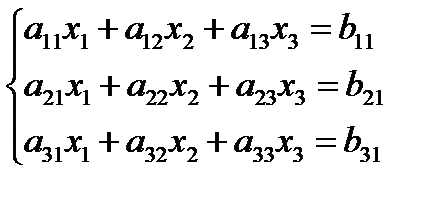
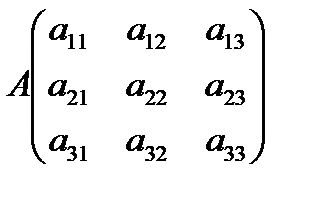
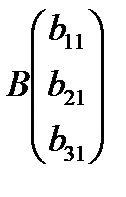
Билет 12.

Билет 13. Бином Ньютона

Возведение двучлена a + b в степень n может быть произведено по формуле называемой разложением бинома Ньютона:

(a + b)ⁿ = aⁿ + C¹_n a^{n - 1} b + C²_n a^{n - 2} b² +...+C^k_n a^{n - k} b^k +... + C^{n - 1}_n ab^{n - 1} + Cⁿ_nbⁿ

или (после подстановки выражений C^k_n с учетом формулы C^k_n = C^{n - k}_n):

,

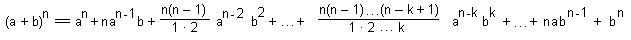где C^k_n — число всех возможных сочетаний, которые можно образовать из n элементов по k.

Пример:
(a + b)⁵ = a⁵ + C¹₅ a⁴b + C²₅ a³b² + C³₅ a²b³ + C⁴₅ ab⁴ + C⁵₅ b⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

Свойства бинома Ньютона

1. Разложение бинома (a + b)ⁿ представляет собой многочлен, расположенный по убывающим степеням a (от n-й до нулевой) и по возрастающим степеням b (от нулевой до n-й); сумма показателей a и b в каждом члене разложения равна показателю степени бинома. Число членов разложения на единицу больше показателя степени бинома.
2. Коэффициенты членов разложения («биноминальные коэффициенты») возрастают до середины разложения и затем убывают; коэффициенты каждой пары членов, равноотстоящих от начала и конца разложения, равны между собой. Если n четное, то имеется один средний наибольший коэффициент; если n нечетное, то имеется два средних наибольших коэффициента.
3. При возведении в n-ю степень разности a - b все четные члены разложения имеют знак "минус":

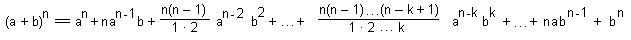
Билет 14. Функция, определение и способы задания. Обратная функция, суперпозиция функций.

Функция

ФУНКЦИЯ 1.Зависимая переменная величина.2.Соответствие y=f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента или независимой переменной) соответствует определенное значение другой величины, y (зависимой переменной или Ф. в значении 1). Ф. задана, если известен закон, определяющий такое соответствие. На практике она задается формулой, таблицей или графиком. При построении графика функции анализируются такие ее свойства, как четность или нечетность, нулевые значения, периодичность, монотонность, наличие асимптоты и др. Важны еще два часто употребляемых понятия: функция, заданная в виде уравнения f(x,y) = 0, неразрешенного относительно y, называется неявной; функция, заданная в виде y= f(g(x)), т. е. функция функции, называется сложной Ф. или иначе — суперпозицией функций g и f. Сложную функцию часто записывают в виде y=f(u), где u=g(x), при этом u называют промежуточным аргументом. Множество X значений аргументов функции x ∈ X называетсяобластьюопределенияфункции, асоответственномножество Y = {y | y = f(x), x ∈ X} —областьюзначенийфункции, илиобластьюизмененияфункции.

Способы задания:

Аналитический :функция задается в виде одной или нескольких формул или уравнений.

Если область определения функции y=f(x) не указана , то предполагается, что она совпадает с множеством всех значений аргумента, при которых соответствующая формула имеет смысл. 1/1+х^2 ( -∞;∞)

Графический:задается график функции.

Табличный:функция задается таблицей ряда значений аргумента и соответствующих значений функции. Известные таблицы значений тригонометрических функций, логарифмические таблицы.

Обратная функция.Функция, обращающая зависимость, выражаемую данной функцией. Так, если у = f (x) — данная функция, то переменная х, рассматриваемая как функция переменной у, х = φ (y), является обратной по отношению к данной функции у = f (x).

Суперпозиция.Несколько функций , используются вместе.

Последовательность Xn называется возрастающей, если X1<X2<X3<…<Xn<…

Последовательность называется убывающей, если X1>X2>X3>…>Xn>…

Последовательность называется невозрастающей, если X1≥X2≥X3≥…≥Xn≥…

Все n последовательности называются монотонными.

Т.Пусть Xn монотонно возрастающая последовательность, если она ограничена сверху, то Xn<M, M = const

Если Xn монотонно убывающая последовательность, она имеет конечный предел, если она ограничена снизу Xn≥m, m=const

Примеры.

1. Ясно, что при x→+∞ функция y=x²+1 является бесконечно большой. Но тогда согласно сформулированной выше теореме функция 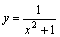– бесконечно малая при x→+∞, т.е. .
2. .

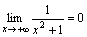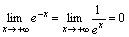Можно доказать и обратную теорему.

Теорема 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y=1/f(x) является бесконечно большой функцией.

Доказательство теоремы проведите самостоятельно.

Примеры.

1. .
2. .
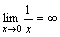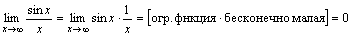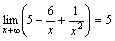3. , так как функци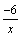и и 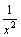- бесконечно малые при x→+∞, то 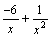, как сумма бесконечно малых функций есть функция бесконечно малая. Функция же 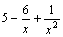является суммой постоянного числа и бесконечно малой функции. Следовательно, по теореме 1 для бесконечно малых функций получаем нужное равенство.

Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A≠ 0

.

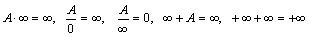ТЕОРЕМЫ О ПРЕДЕЛАХ

Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.

.

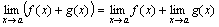Доказательство. Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится так же. Пусть 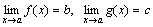.Тогда f(x)=b+α(x) иg(x)=c+β(x), где α и β – бесконечно малые функции. Следовательно,

f(x) + g(x)=(b + c) + (α(x) + β(x)).

Так как b + cесть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то

.

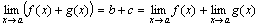Пример. .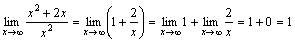

Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:

.

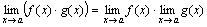Доказательство. Пусть 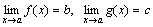. Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и

fg = (b + α)(c + β) = bc + (bβ + cα + αβ).

Произведение bc есть величина постоянная. Функция bβ + c α + αβ на основании свойств бесконечно малых функций есть величина бесконечно малая. Поэтому .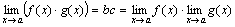

Следствие 1. Постоянный множитель можно выносить за знак предела:

.

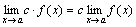Следствие 2. Предел степени равен степени предела:

.

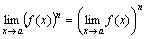Пример. .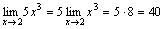

Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.

.

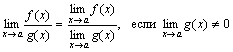Доказательство. Пусть 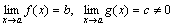. Следовательно, f(x)=b+α(x) и g(x)=c+β(x), где α, β – бесконечно малые. Рассмотрим частное

.

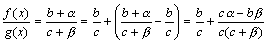Дробь 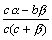является бесконечно малой функцией, так как числитель есть бесконечно малая функция, а знаменатель имеет предел c²≠0.

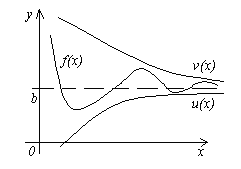Теорема 4. Пусть даны три функции f(x), u(x) и v(x), удовлетворяющие неравенствам u(x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x) стремится к тому же пределу, т.е. если

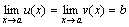, то .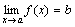

Смысл этой теоремы понятен из рисунка.

Доказательство теоремы 4 можно найти, например, в учебнике: Пискунов Н. С. Дифференциальное и интегральное исчисления, т. 1 – М.: Наука, 1985.

Теорема 5. Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b, то этот предел не может быть отрицательным: b≥0.

Доказательство. Доказательство проведем методом от противного. Предположим, что b<0, тогда |y – b|≥|b| и, следовательно, модуль разности не стремится к нулю при x→a. Но тогда y не стремится к пределу b при x→a, что противоречит условию теоремы.

Теорема 6. Если две функции f(x) и g(x) при всех значениях аргумента x удовлетворяют неравенству f(x)≥ g(x) и имеют пределы 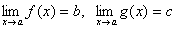, то имеет место неравенство b≥c.

Доказательство. По условию теоремы f(x)-g(x) ≥0, следовательно, по теореме 5 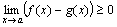, или .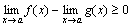

Ограниченная последовательность. Последовательность 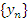называется ограниченной сверху, если существует такое число U, что 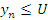для любых номеров n. При этом число U называется верхней границейпоследовательности.

Последовательность 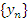называется ограниченной снизу, если существует такое число L, что 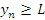для любых номеров n. Число L называется нижней границейпоследовательности.

Последовательность 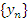называется ограниченной, если существуют такие числа L и U, что 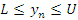для всех n = 1,2,3,…

Теорема 1. Любая ограниченная сверху последовательность имеет наименьшую верхнюю границу.
Теорема 2. Любая ограниченная снизу последовательность имеет наибольшую нижнюю границу.

Свойства пределов.

1. Финально постоянная последовательность сходится.
2. Если последовательность сходится, то предел единственен.
3. Сходящаяся последовательность ограничена.

Доказательство.

1. Если x_n = A при n>N, то для любой окрестности U(A) имеем x_nО U(A) при n>N, то есть lim _n®Ґx_n = A.
2. Пусть lim_n®Ґx_n = A₁ и lim_{n® Ґ}x_n = A₂, A₁№ A₂, тогда выберем e - окрестности точек A₁, A₂, так чтобы они не пересекались. В качестве e можно взять число e = 1/2|A₁-A₂|. По определению предела $ N₁,N₂, что при n>N₁ x_nОU(A₁), а при n>N₂ x_nО U(A₂). Следовательно, при n>max{N₁,N₂} x_nО U(A₁)ЗU(A₂), что невозможно, так как U(A₁)З U(A₂) = Ж.
3. Пусть lim_n®Ґx_n = A, положим в определении предела e = 1, тогда " n>N |x_n-A|<1 значит |x_n|<|A|+1. Выберем C>max{|x₁|,...,|x_N|,
   |A|+1}, тогда получим, что при " nО N |x_n|< C.

Односторонние пределы.

Считается, что х стремится к х₀ любым способом: оставаясь меньшим, чем х₀ (слева от х₀), большим, чем х₀ (справа от х₀), или колеблясь около точки х₀.

Число А₁ называется пределом функции y=f(x) слева в точке х₀, если для любого ε<0 существует число σ=σ(ε)>0 такое, что при х?(x₀-σ;x₀), выполняется неравенство |f(x)-A₁|<ε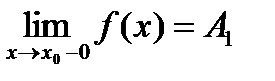

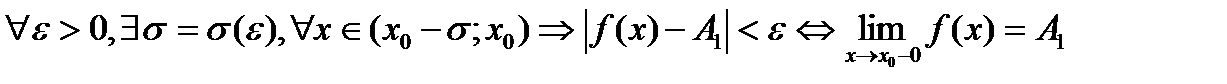
Свойства пределов.

1) если предел 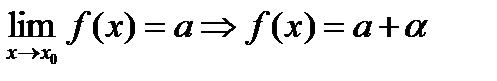функция равна этому числу плюс б.м.

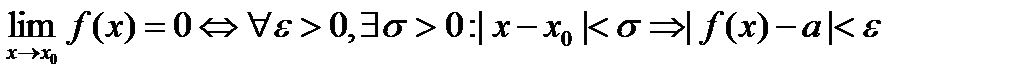
ε – сколь угодно малое число

|f(x)-a|=α; f(x)=a+ α

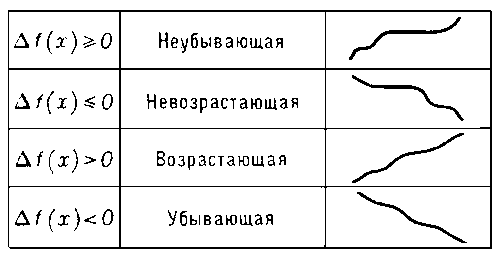
Монотонные функции.

функция, приращения которой Δf(x) = f(x’) — f(x) при Δx = x’ — x > 0 не меняют знака, т. е. либо всегда неотрицательны, либо всегда неположительны. Выражаясь не совсем точно, М. ф. — это функции, меняющиеся в одном и том же направлении. Различные типы М. ф. представлены на прилагаемой табл.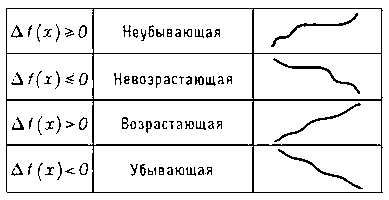

Например, функция у = x³ является возрастающей функцией. Если функция f(x) имеет в каждой точке производную f’(x), которая неотрицательна и обращается в нуль лишь в конечном числе отдельных точек, то f(x) — возрастающая функция. Аналогично, еслиf’(x) ≤ 0 и обращается в нуль только в конечном числе точек, то f(x) — убывающая функция.

Условие монотонности может выполняться как для всех х, так и для х из некоторого интервала (или отрезка). В этом последнем случае функцию называют монотонной на этом интервале (или отрезке). Например, функция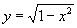

М. ф. представляют собой один из простейших классов функций и постоянно встречаются в математическом анализе и теории функций. Если f(x) — М. ф., то для любого x₀ существуют пределы

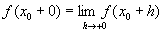
и

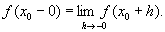
Билет 18.

Замечательные пределы.

Замечательный предел.

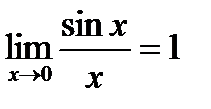
Замечательный предел.

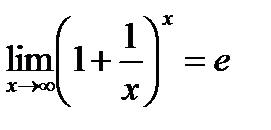
Пусть х→∞. Каждое значение х заключено между двумя положительными целыми числами:

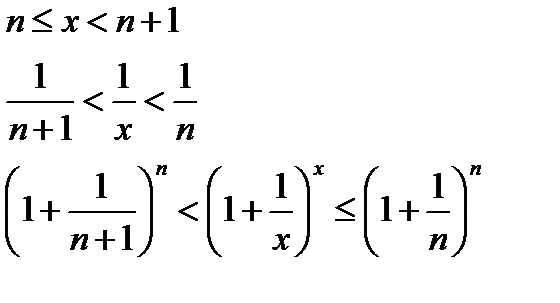
Если x→∞, то n→∞, тогда

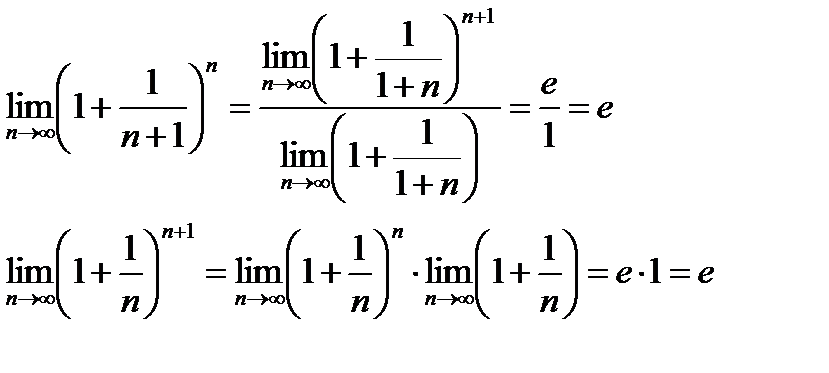
По признаку о существовании пределов:

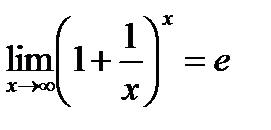
Билет 20.

Теорема Ролля,Теорема Ферма

Теорема Ро́лля (теорема о нуле производной) утверждает, что

Если вещественная функция, непрерывная на отрезке[a,b] и дифференцируемая на интервале(a,b) , принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.

Доказательство

Если функция на отрезке постоянна, то утверждение очевидно, поскольку производная функции равна нулю в любой точке интервала.

Если же нет, поскольку значения функции в граничных точках сегмента равны, то согласно теореме Вейерштрасса, она принимает своё наибольшее или наименьшее значение в некоторой точке интервала, то есть имеет в этой точке локальный экстремум, и по лемме Ферма, в этой точке производная равна 0.в интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.

Теорема Ролля:пусть

1)f(x)определена и непрерывна на промежутке[a,b]

2)сущ-ет конечная производная f’(x)в интервале(a,b)

3)на концах f(a)=f(b),тогда сущ-етС,а<C<bf’(c)=0 m<=f(x)<=M

Функция достигает наибол. И наименьш. Зн-е дельтаm=Mотсюда следует f(x)=const отсюда следует f’(x)=0

2m не равно M

На концах значения одинаковые ,то или мин или максимальное достигают во внутренней точке то по теор. Ферма в этой точке производная равна нулю

Теорема Ферма:
Пусть ф-яf(x)определена в некоторых промежутках Х и во внутренней точке С принимает наибольшее (наименьшее)значение ,тогда f’(x)=0

Теорема Коши

1)Пусть f(x),g(x) определены на [a,b]

2)сущ-ют производныеf’(x),g’(x) на интервале(a,b)

3)g’(x) не равно 0,любое Х э [a,b],тогда

Существует С, a<c<b, f’(c)/g’(c)=f(b)-f(a)/g(b)-g(a)

Док-во

g(b) не равно g(a)

составимвспомогательнуюфун-июF(x)=f(x)-f(a)-f(b)-f(a)/g(b)-g(a)*(g(x)+g(a)) непрерывнаF’(x)=f’(x)-f(b)-f(a)/g(b)-g(a)*g’(x)

F(a)=f(a)-f(a)-(f(b)-f(a)/g(b)-g(a))*(g(a)-g(a))=0

F(b)=f(b)-f(a)-(f(b)-f(a)/g(b)-g(a))*(g(b)-g(a))=0

Сущ-етСF’(c)=0 отсюдаследуетf’(c)-(f(b)-f(a)/g(b)/g(a))*g’(c)=0

F’(c) /g’(c)=f(b)-f(a)/g(b)-g(a)

ФормулаЛейбница

Пусть y=f(x) дифференцируема функция, а ее аргумент х – независимая переменная. Тогда дифференциал dy=f ′(x)dx есть также функция х, можно найти дифференци-ал этой функции. Дифференциал от дифференциала есть второй дифференциал.

Производную можно рассматривать, как отношение дифференциала соответствующего порядка к соответ-ствующей степени дифференциала независимой пере-менной.

Дифференциал n-ого порядка, есть дифференциал от дифференциала (n-1)-ого порядка, т.е. производную функции можно рассматривать, как отношение ее диф-ференциала соответствующего порядка к соответству-ющей степени дифференциала независимой перемен-ной.

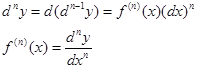
Понятие производной произвольного порядка задаётся рекуррентно. Полагаем

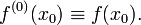
Если функция дифференцируема в , то производная первого порядка определяется соотношением

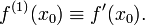
Пусть теперь производная -го порядка определена в некоторой окрестности точки и дифференцируема. Тогда

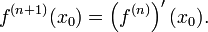
Если функция имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от может иметь в некоторой точке частные производные по той же или по любой другой переменной. Для исходной функции эти производные будут частными производными второго порядка (или вторыми частными производными).

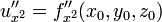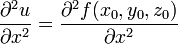
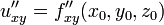или

или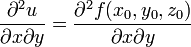

Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,

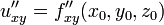
Формула Лейбница

Y^(n)=(U*V)^n=Сумма (от nдоk=0) U^(n-k)*V^(k)

Вторая производная для функции, заданной параметрически

(f’(x))’-производная второго порядка

F’’(x); Y’’=d^2y/dx^2

29. Правило Лопиталя:

Правило Лопита́ля — метод нахождения пределов функций, раскрывающий неопределённости вида и . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

Условия

1. 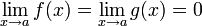или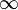

2.f(x)и g(x)дифференцируемы в проколотой окрестности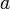

3. 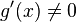в проколотой окрестности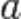

4. существует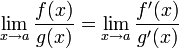

Пределы также могут быть односторонними.

Теорема.

Пустьf(x),g(x) непрерывны и дифференцируемы в окрестности т.а и равны нулю в этой точке. Пусть g’(a)не равно нулю,тогда если сущ-етlimf’(x)/g’(x)=l,то limf(x)/g(x)= limf’(x)/g’(x)=l

Замечание 1.

Теорема верна в том случае,если ф-и f(x) и g(x) не определены в точке а,носущ-етlimf(x)=0,limg(x)=0

Замечание 2.

Т.верна в том случае,если х принадлежит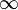

Замечание 3

Если limf’(x)/g’(x)=0/0 дифференцирование можно повторить еще раз

Билет 1

Множества - совокупность некоторых объектов объединённых по какому-либо признаку.

Операции с множествами: объединение, пересечение, относительное дополнение от А до В, симметричная разность, абсолютное дополнение

Объединение множеств - множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств AUB

Пересечение множеств – множество, состоящее из элементов, каждый из которых принадлежит множеству А или множеству В

Относительное дополнение от А до В

Симметричная разность А+В=(А\В)U(B\A)

Абсолютное дополнение A=V\A

Билет 2

Вещественные (действительные) числа – множество всех бесконечных десятичных дробей

Свойства

a+b=b+a a=b,b=c => a=c

(a+b)+c=a+ (b+c) a>b,b>c => a>c, a>b => a+c>b+c, a>0,b>0 => ab>0

ab=ba Непрерывность вещ.чисел a>b => -a<-b

(ab)c=a(bc) a>b => a-b>0

(a+b)c=ac+bc a+(-b)+(-a)>0+(-a)

0+a=a a+(-a)+(-b)>-a

a+(-a)=0 0+(-b)>-a

1*a=a -b>-a

a не равно 0 => a*a(в -1 степени)=1

Билет 3

Абсолютная величина числа – расстояние от числа до нуля

Свойства

Модуль х больше либо равен 0

Модуль х равен модулю -х

Модуль х со знаком – за модулем меньше либо равно х или меньше либо равно модулю х

Теорема 1

Теорема 2

Билет 4

- существует, - для любого

1^2+2^2+3^2+…+n^2=n(n+1)(2n+1)/6 n

1) n=1 1^2=1(1+1)(2+1)/6=1

2) n => n+1

Билет 5

Определитель – число detА квадратной матрицы А порядка n

а(11) a(12) … a(1n)

a(21) a(22) … a(2n)

a(n1) a(n2) … a(nn)

Свойства

1.Значение определителя не изменится от замены строк столбцами

2.Определитель с двумя одинаковыми рядами равен нулю

3.Если все элементы какого-нибудь ряда умножить на одно то же число, то значение определителя умножится на это же число

4.Если все элементы какого-нибудь ряда обладают общим множителем, то этот множитель можно вынести за знак определителя

5.Определитель с двумя пропорциональными рядами равен нулю

6.Если элементы какого-либо ряда определителя представляет собой сумму двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей

7.

8.Если в определители поменять местами два ряда, то он изменит знак, а по модулю не изменит

Билет 6

Минор элемента а- определитель, который получается из первоначального путём вычёркивания строки и столбца проходящих через данный элемент

Алгебраическим дополнением А а- (-1)^i+j М

Теорема 1: Если в определители порядка n все элементы строчки i (или столбца) равны 0, кроме элемента а, то значение определителя равно А а

Теорема 2: Какую бы строчку или столбец определителя порядка n мы не взяли, значение определителя равно сумме произведений элементов этой строки или столбца на их алгебраическое дополнение

Билет 7

Матрица- прямоугольная таблица чисел, содержащая m строк одинаковой длины или n столбцов одинаковой длины

Действия с матрицами:

Сложение

2 -1 4 1 1 -3 3 0 -1

3 0 8 0 11 2 3 11 10

Умножение на число

2А+5В= 16 25

13 -8

А= 3 5 В= 2 3 2А= 6 10 5В= 10 15

4 1 -1 2 8 -2 -5 10

Произведение

А= 1 3 2 В= 1 3 6 1

1 6 4 2 3 4 1

2 5 1 3

С(11)=1*1+3*2+2*2=11

С(12)=1*3+3*3+2*5)=22 С= 11 22 20 10

С(13)=1*6+3*4+2*1=20 21 41 34 19

С(14)=1*1+3*1+2*3=10

С(21)=1*1+6*2+4*2=21

С(22)=1*3+6*3+4*5=41

С(23)=6*1+6*4+4*1=34

С(24)=1*1+6*1+4*3=19

Билет 8

Транспортирование- поворот вокруг главной диагонали

А= a(11) a(12) … a(1n) A^T= a(11) a(21) a(m1)

a(21) a(22) … a(2n) a(21) a(22) a(m2)

a(m1) a(m2) … a(mn) a(1n) a(2n) a(mn)

Свойства

1.(А+В)^T=A^T+B^T

2.(A*B)^T=A^T*B^T

Обратная матрица – всякая невырожденная матрица. Существует только для квадратной

А= a(11) a(12) … a(13) A^*= a(11) a(21) a(31)

a(21) a(22) … a(23) a(12) a(22) a(32)

a(31) a(32) … a(33) a(13) a(23) a(33)

Свойства

1.A^-1*A=A*A^-1=E (обратная матрица)

2.A^-1=1/detA (A^*)^t (квадратная матрица)

Теорема: Если для матрицы существует обратная матрица, то она единственная

Билет 9

Ранг матрицы - наибольший из порядков миноров данной матрицы, отличных от нуля. Обозначается r(A)

Свойства ранга матрицы

1.при транспортировании матрицы её ранг не меняется

2.если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится

3.ранг матрицы не изменяется при элементарных преобразованиях матрицы

Элементарные преобразования матрицы

1.перестановка строк

2.умножение элементов какой-нибудь строки на ненулевое число

3.прибавление к элементам одной строки элементов другой строки умножается на одно и то же число

Ступенчатая матрица- матрица, где каждая строка имеет хотя бы один ненулевой элемент, если ненулевой элемент каждой строки, начиная со второй, расположен правее ненулевого элемента предыдущей строки

Теорема: Любую матрицу A с помощью элементарных преобразований можно преобразовать в ступенчатую матрицу

Билет 10

Для того, чтобы система однородных линейных уравнений имела нетревиальное решение, необходимо чтобы ранг её основной матрицы А был меньше числа неивестного
1.Несовместные линейные уравнения- не имеют решения.
2.Совместные-решение есть
А)Определённые- одно решение
Б)Неопределённые- решений бесконечно много

Метод Крамера
Xj=Дельтаj/дельта, j=1,2,3

Матричный метод

X=A^-1*B

Билет 11. Метод Гаусса решения систем линейных уравнений.

Метод Гаусса.

Сначала следует привести систему к треугольному (ступенчатому) виду, а затем ступенчато решить.

Формула Крамера.