Линейные однородные дифференциальные уравнения с постоянными коэффициентами

Для уравнений 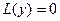(1),

у которых 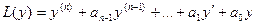(.2),

где 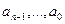- постоянные величины, существует способ, с помощью которого задачу нахождения фундаментальной системы решений можно свести к задаче нахождения корней некоторого вспомогательного алгебраического уравнения.

Для этого будем искать решения уравнения 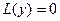в виде 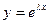. При этом 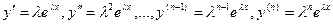(.3).
Подставим полученные величины в уравнение (1):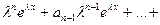
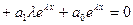, или 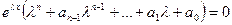. Поскольку 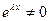при всех , из этого уравнения следует, что 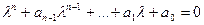(4).

Таким образом, функция 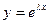удовлетворяет уравнению (1) тогда и только тогда, когда 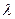удовлетворяет уравнению (4). Уравнение (4) называется характеристическим уравнениемуравнения (1).

Далее мы установим вид фундаментальной системы решений уравнения (1) в зависимости от свойств корней уравнения (4).

Случай 1. Пусть все корни уравнения (4) действительные и различные. Обозначим их 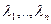и рассмотрим функции 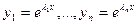, являющиеся решениями уравнения (1) по доказанному выше. Докажем линейную независимость. Это будет означать, что 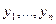- фундаментальная система решений (1). Определитель Вронского этой системы функций равен, с учетом (2)
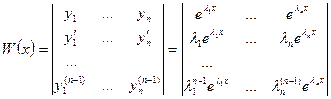или, после вынесения из столбцов множителей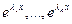 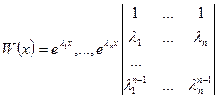. Определитель 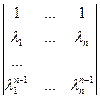представляет собой известный определитель Вандермонда. Он равен 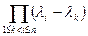. Поэтому если все числа 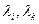попарно различны, этот определитель не равен 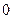. Следовательно, функции 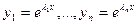линейно независимы и составляют искомую фундаментальную систему решений.

2 случай. Все корни 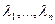- различные, но среди них есть комплексные числа. Формально 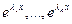- это снова фундаментальная система решений уравнения, т.к. эти функции линейно независимы (их определитель Вронского, как и в случае 1, отличен от 0). Однако мы рассматриваем уравнение с действительными коэффициентами и нам было бы желательно построить фундаментальную систему решений, состоящую из действительных функций.

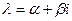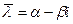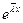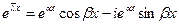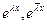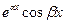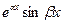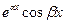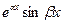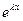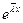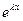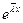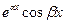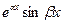Пусть - любой комплексный корень уравнения (4). Поскольку (.4) имеет действительные коэффициенты, число также является его корнем. Значит - тоже решение уравнения (1).Легко видеть, , т.е. являются линейными комбинациями и . Разумеется, и также можно линейно выразить через и . Поэтому линейная независимость решений и с остальными решениями уравнения (19.1) равносильна линейной независимости и с остальными решениями.

Подведем итоги. В случае, когда все 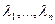- различные, причем 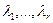- действительные, а 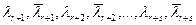- пара комплексно сопряженных чисел 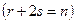, причем 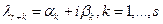, то фундаментальная система решений уравнения (1) имеет вид: , .

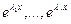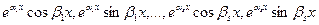Случай 3. Корни характеристического уравнения действительные, но среди них есть кратные. Напомним, что число 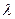называется корнем многочлена 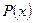кратности 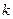, если 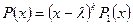, где 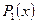- многочлен, причем .

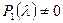Пусть корни 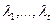имеют, соответственно, кратности 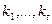. Тогда можно доказать (но мы оставим это без доказательства), что функции
,
,
…

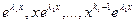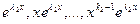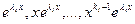
составляют фундаментальную систему решений уравнения (.1)

Пример. Приведем пример, подтверждающий это утверждение. Уравнению 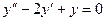соответствует характеристическое уравнение 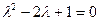, 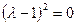. Оно имеет корень 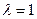с кратностью 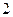. Рассмотрим функци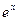и и 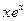. 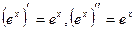и подставляя 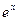в исходное уравнение, получаем 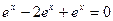, т.е. верное равенство. Далее, 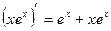, 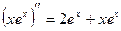и подстановка функции 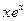в уравнение дает верное равенство: 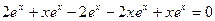. Итак, 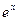и 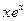- действительно решения уравнения 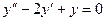. Эти функции линейно независимы, т.к. из равенства 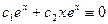при 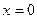следует 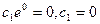. Значит, 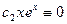. Тогда при .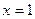

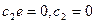В случае 4, когда действительные корни 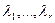уравнения (.1) имеют кратности 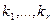, а комплексные корни 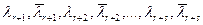имеют кратности 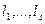, можно доказать, что функции
,
…
,
,
,
…
,
,
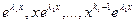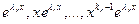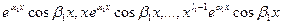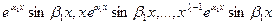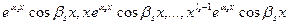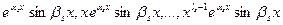образуют фундаментальную систему решений уравнения (1).